Google DeepMind のミレニアム賞に対する新しい AI アプローチは、3 つの流体方程式における新しい不安定な特異点を発見することを目指しています。

今年5月末には、数学者のハビエル・ゴメス・セラーノ氏がインタビューで、グーグル・ディープマインドと協力して「人類が知る最も難解なパズルの一つであるナビエ・ストークス方程式をできるだけ早く解こうとしています。」この方程式はクレイ数学研究所が授与する7つのミレニアム懸賞問題のうちの1つであり、解いた人には100万ドルの賞金が与えられる。

ハビエル・ゴメス・セラーノらが開始した「ナビエ・ストークス作戦」と呼ばれるプロジェクトは3年間にわたり、20人のチームによって実行され、常に極秘にされてきたと報じられている。しかし、Google DeepMindの責任者であるデミス・ハサビス氏も、今年1月のインタビューで次のように明らかにしている。彼は「ミレニアム賞に値する問題を解こうとしている」と述べたが、それが何なのかは明言しなかった。「1年か1年半以内には答えがわかるだろう」

現在、この謎の作戦は徐々に明らかになりつつあるようだ。

Google DeepMind は、ニューヨーク大学、スタンフォード大学、ブラウン大学などの研究機関と共同で、機械学習フレームワークと高精度のガウス・ニュートン最適化装置を開発した。3つの異なる流体方程式において、新たな不安定特異点が初めて体系的に発見されました。爆発率と不安定性順序を結び付ける簡潔な経験的漸近式が明らかにされています。

実験結果によれば、この方法は、見つかったすべての解決策に関して、既存の研究よりも大幅に優れた精度を達成しました。特定の CCF ソリューションの場合、結果は倍精度浮動小数点のマシン限界にさらに近く、GPU ハードウェアの丸め誤差によってのみ制限されるため、非線形偏微分方程式 (PDE) の複雑な状況を調査するための新しい研究パラダイムが提供され、数理物理学における長年の問題を克服するための新しい道が開かれます。

関連研究は「不安定な特異点の発見」と題され、arXiv にプレプリントとして公開されています。

用紙のアドレス:
https://go.hyper.ai/iGh6t
論文全文をダウンロードするには、公式アカウントをフォローし、「不安定な特異点」と返信してください。

2段階構造を発見・分析し、不安定な特異点を見つける

人類による自然法則の探究の歴史を振り返ると、流体力学は常に最も複雑で挑戦的な分野の一つでした。何世紀にもわたり、数学者たちはハリケーンの渦から飛行機の翼の揚力に至るまで、あらゆる物理法則を複雑な方程式を用いて記述してきました。しかし、流体において特異点や爆発が生じるかどうかは、数学における最も根本的かつ未解決の問題の一つです。この現象とは、支配方程式（3 次元オイラー方程式など）の解が滑らかな初期条件から始まる場合、無限勾配が発生する可能性があります。

従来の数値解析手法では、主に安定特異点を同定します。安定特異点は、初期条件にわずかな摂動を加えても形成されうるロバストな結果です。一方、不安定特異点は、初期条件を無限に正確に調整する必要があるため、捕捉が極めて困難です。なぜなら、この非常に不安定な状態では、小さな摂動でもすぐに解が爆発の軌道から外れてしまうからです。しかし、境界のないオイラーやナビエ・ストークスの問題など、いくつかの重要な未解決問題に関しては、不安定な特異点が重要な役割を果たしている可能性があるという推測が数学界で広まっています。

この一世紀も未解決の問題に対して、研究者たちは、解決策の発見と解決策の分析という 2 つの段階を経ました。不安定特異点の高精度な発見を実現します。

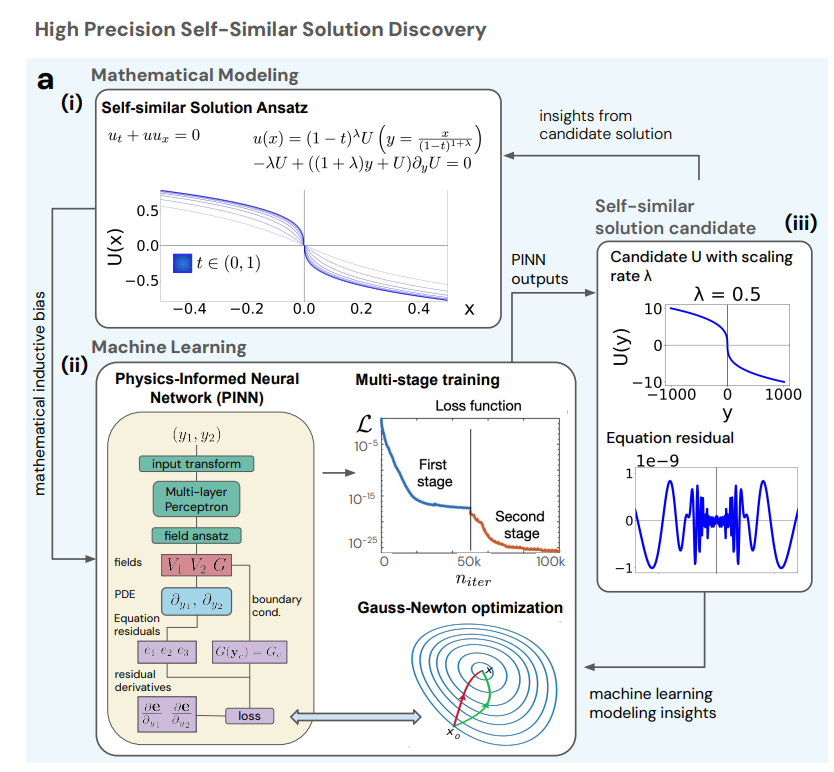
初め、研究者らは、バーガース方程式に対し、図(i)に示すように、自己相似なスケーリング係数λとその自己相似な空間分布を持つ爆発的解を候補解を用いて探索した。その後、反復的なアプローチを用いて、機械学習プロセスと解の精度を継続的に最適化した（図(ii)参照）。候補解の実験結果と精度は、数理モデリングとニューラルネットワークアーキテクチャの設計に役立ち、さらに入力座標変換や出力フィールドの形態学的設計といったネットワークアーキテクチャにおける帰納的バイアスにも影響を与えた。

このプロセスでは、研究者らは、ガウス・ニュートン最適化装置と多段階トレーニング戦略を組み合わせた物理情報ニューラルネットワーク（PINN）を使用して、正しいスケーリング率λを見つけながら高精度の候補ソリューションを生成しました。

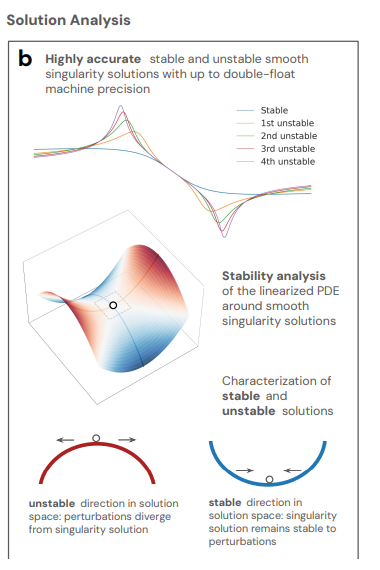
第二に、解の解析において、CCF方程式、IPM方程式、およびブシネスク方程式で発見された不安定解それぞれについて、研究者らはその周りの偏微分方程式を線形化することでその安定性を分析した。発見されたn番目の不安定解ごとに、研究者らは解と同じ対称性仮定を共有するn個の不安定モードを発見した。

これらの不安定モードは、解をより安定へと導く方向を示しており、検討されたλの許容値の範囲内で、発見された解の族が完全であることを示しています。これにより、研究者は安定性の程度だけでなく、安定特異点と不安定特異点の発見を高精度に特徴付けることができます。

数学的洞察とニューラルネットワークがPINNを新たな武器にする

本研究では、物理情報ニューラルネットワークに新たな力が与えられ、偏微分方程式を解くための汎用ツールとしての典型的な役割を超えた。研究チームは、解をニューラルネットワークによってパラメータ化された滑らかな関数として表現した。数学的洞察をニューラル ネットワーク アーキテクチャに直接埋め込むことができ、最適化プロセスを数学的に適切なソリューションへと導きます。

研究チームは、対称性、周期性、無限領域の扱いといった支配方程式から導かれる制約をアーキテクチャ設計によって強制することで、学習のための堅牢な標準訓練パラメータを提供しました。数値実験と数学的解析のフィードバックループを通してネットワークアーキテクチャを反復的に最適化することで、この挙動を明示的に考慮し、残りの方程式を書き直すことで、最適化の安定性を大幅に向上させました。

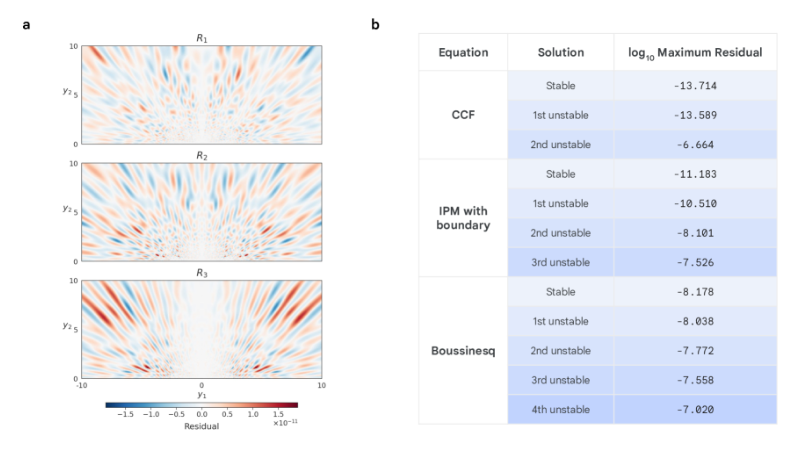
高精度トレーニングの改善

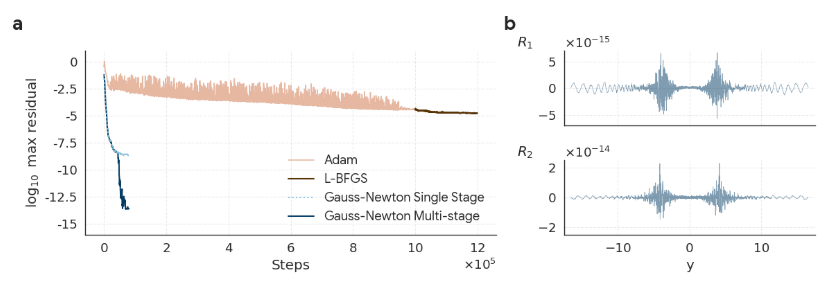
不安定な特異点に要求される極めて高い精度を満たすために、研究者らはトレーニング プロセスに 2 つの重要な改良を加えました。高精度のトレーニングのために、ガウス・ニュートン最適化装置と多段階トレーニングが導入されています。

この最適化手法を採用した理由は、現在一般的な標準的な勾配最適化手法（AdamやL-BFGSなど）では、方程式の高品質な解を生成するのに不十分であるためです。そのため、研究チームはニューラルネットワークの最適化に、より強力なガウス・ニュートン最適化法を選択しました。ネットワークのサイズが小さいため、この従来不可能だった解決策が成功しました。実験結果によると、ガウス・ニュートン法は約5万回の反復で残差誤差を10⁻⁸まで低減できることが示されています。標準の勾配オプティマイザーと比較すると、パフォーマンスが向上し、収束が大幅に速くなります。

要するに、多段階トレーニングの考え方は、まず 1 つのネットワークをトレーニングして近似解を取得し、次に 2 番目のネットワークをトレーニングして、前のネットワークが適切に処理できなかったエラーを具体的に修正するというものです。2つのネットワークの出力を組み合わせることで、解の精度を向上させることができます。CCF方程式とIPM方程式の安定解と一次不安定解を用いた実験では、多段階学習法によって最大残差が5桁改善され、CAPに基づく厳密な数学的検証を満たすのに十分な精度が得られました。

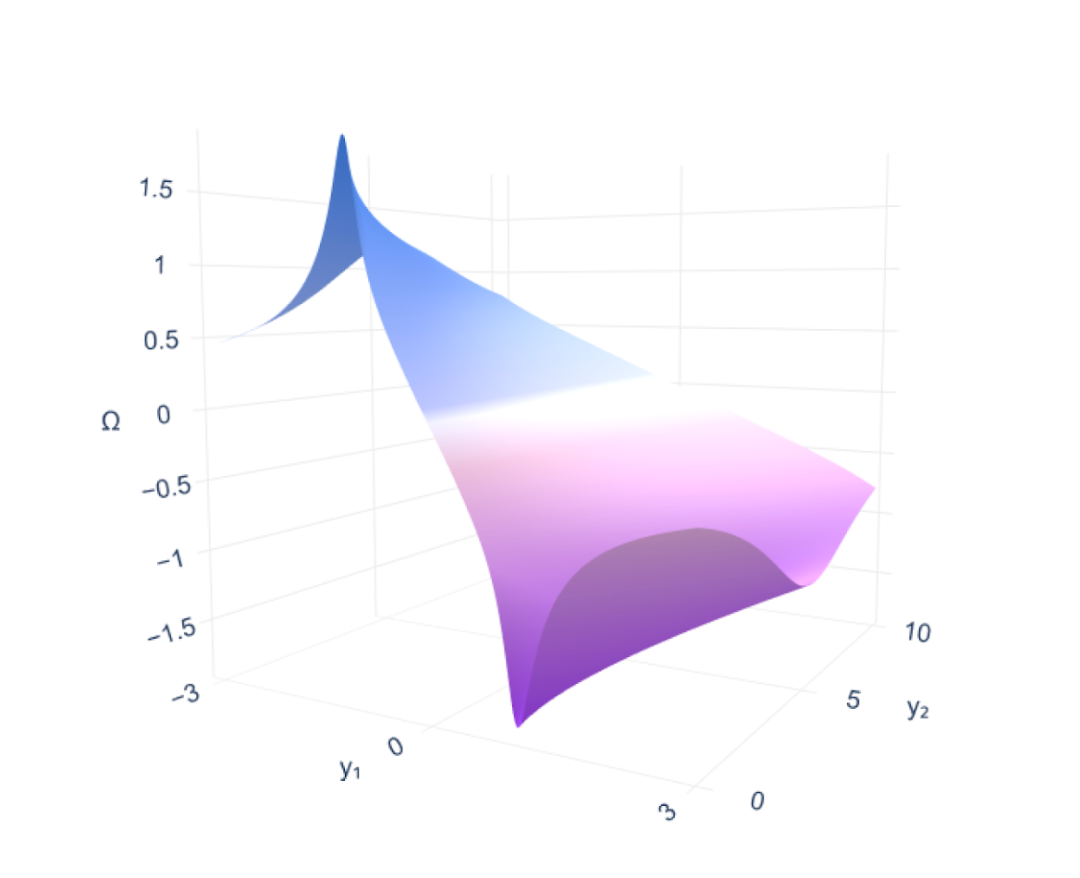
このアプローチにより、モデルの精度は新たなレベルに到達しました。研究チームは、2次元渦度場の3次元可視化と解析を参考例として用い、各点における流体の回転角度の測定を実証しました。これにより、地球の直径の予測精度を数センチメートル以内に向上させるのに匹敵する最大誤差が解消されました。

論文 1 中国の博士として

本論文の筆頭著者であるYongji Wang氏は、現在ニューヨーク大学クーラント数学研究所のポスドク研究員であり、スタンフォード大学の客員ポスドク研究員も務めています。彼の研究分野は連続体力学、地球物理学、科学的機械学習であり、自然界や環境における複雑な物理プロセスの解明に理論および数値的手法を応用する豊富な経験を有しています。

この研究は、南極の氷棚の隠れた物理的特性を明らかにすることから、非線形偏微分方程式 (PDE) の自己相似爆発解を見つけることまで、さまざまな科学的問題に対する高精度のディープラーニング技術の開発に重点を置いています。

参考文献:
1.https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/
2.https://english.elpais.com/science-tech/2025-06-24/spanish-mathematician-javier-gomez-serrano-and-google-deepmind-team-up-to-solve-the-navier-stokes-million-dollar-problem.html

3.https://mp.weixin.qq.com/s/CRlGLmji4BWNkNaA7e2JEw