In der wissenschaftlichen Datenverarbeitung und der Ingenieursimulation stellt die effiziente und präzise Vorhersage der Entwicklung komplexer physikalischer Systeme seit jeher eine zentrale Herausforderung für Wissenschaft und Industrie dar. Obwohl traditionelle numerische Methoden theoretisch die meisten physikalischen Gleichungen lösen können, sind sie bei hochdimensionalen, multiphysikalischen Szenarien oder inhomogenen Randbedingungen rechenaufwändig und eignen sich nur bedingt für die gleichzeitige Bearbeitung umfangreicher Aufgaben.Inzwischen haben Durchbrüche beim Deep Learning in der Verarbeitung natürlicher Sprache und im Computer Vision Forscher dazu veranlasst, die Möglichkeit der Anwendung von „Basismodellen“ in physikalischen Simulationen zu untersuchen.

Physikalische Systeme entwickeln sich jedoch häufig über mehrere zeitliche und räumliche Skalen hinweg, während die meisten Lernmodelle typischerweise nur auf kurzfristige Dynamiken trainiert werden. Werden sie für Langzeitprognosen verwendet, akkumulieren sich Fehler in komplexen Systemen, was zu Modellinstabilität führt.Darüber hinaus führen unterschiedliche Skalen und Systemheterogenität zu variierenden Anforderungen an Modellauflösung, Dimensionalität und physikalische Feldtypen bei nachgelagerten Aufgaben. Dies stellt eine erhebliche Herausforderung für moderne Trainingsarchitekturen dar, die feste Eingabeformate bevorzugen. Daher beschränken sich die meisten der bisher für Simulationen verwendeten Basismodelle weiterhin auf relativ homogene Datenszenarien, beispielsweise die Behandlung zweidimensionaler Probleme anstelle realistischerer dreidimensionaler Situationen.

Vor diesem Hintergrund stellte ein Forschungsteam der Polymathic AI Collaboration eine Reihe neuer Methoden vor, um die zuvor genannten Herausforderungen zu bewältigen, darunter: Patch-Jittering, lastverteilte Trainingsstrategien für 2D-3D-Szenarien und adaptive Tokenisierungsmechanismen.Auf dieser Grundlage entwickelte das Forschungsteam ein fundamentales Modell namens Walrus, das 1,3 Milliarden Parameter besitzt, Transformer als Kernarchitektur nutzt und hauptsächlich auf die Dynamik von fluidartigen Kontinuumsprozessen ausgerichtet ist. Walrus deckt in seiner Vortrainingsphase 19 sehr unterschiedliche physikalische Szenarien ab, die verschiedene Bereiche wie Astrophysik, Geowissenschaften, Rheologie, Plasmaphysik, Akustik und klassische Fluiddynamik umfassen. Experimentelle Ergebnisse zeigen, dass Walrus bisherige Basismodelle sowohl bei kurz- als auch langfristigen Vorhersagen für nachgelagerte Aufgaben übertrifft und eine stärkere Generalisierungsleistung über die gesamte Verteilung der Vortrainingsdaten hinweg aufweist.

Die zugehörigen Forschungsergebnisse mit dem Titel „Walrus: A Cross-Domain Foundation Model for Continuum Dynamics“ wurden als Preprint auf arXiv veröffentlicht.

Forschungshighlights:

Walrus verfügt über einen Modellparameterbereich von 1,3 Milliarden, innovative Stabilisierungstechniken und die Fähigkeit, die Berechnung an die Problemkomplexität anzupassen;

* Es befasst sich mit mehreren Einschränkungen aktueller fundamentaler Modelle für die Kontinuumsdynamik, wie etwa Kostenanpassung, Stabilität und effizientes Training auf sehr heterogenen Trainingsdaten in nativer Auflösung;

* Walrus ist das bisher genaueste Basismodell für Kontinuumssimulationen und erzielt bei 56 von 65 erfassten Metriken in 26 einzigartigen Kontinuumssimulationsaufgaben aus verschiedenen wissenschaftlichen Bereichen und über verschiedene Zeitskalen hinweg hervorragende Ergebnisse.

Papieradresse:https://arxiv.org/abs/2511.15684
Folgen Sie unserem offiziellen WeChat-Konto und antworten Sie im Hintergrund mit „Mediensimulation“, um das vollständige PDF zu erhalten.

Weitere Artikel zu den Grenzen der KI:
https://hyper.ai/papers

Erstellung heterogener, multidimensionaler, qualitativ hochwertiger Datensätze

Der Erfolg von Walrus ist untrennbar mit der Vielfalt und Qualität der Daten verbunden. Das Forschungsteam nutzte für das Vortraining einen hybriden Datensatz aus Well und FlowBench. Der Well-Datensatz liefert eine große Menge hochauflösender Daten aus realen wissenschaftlichen Fragestellungen, während FlowBench geometrisch komplexe Hindernisse in Standard-Fluid-Szenarien einführt und dem Modell so die Möglichkeit bietet, komplexe Strömungsmuster zu erlernen.

Das Forschungsteam nutzte insgesamt 19 Datensätze, die 63 Zustandsvariablen umfassten, darunter verschiedene Gleichungen, Randbedingungen und physikalische Parametrisierungseinstellungen.Die Daten umfassen sowohl zwei als auch drei Dimensionen, um die Generalisierungsfähigkeit des Modells über verschiedene räumliche Dimensionen hinweg zu gewährleisten. Zur Überprüfung der Übertragbarkeit des Modells optimierte das Forschungsteam es nach dem Vortraining anhand eines Teils der reservierten Datensätze, darunter Daten von Well, FlowBench, PDEBench, PDEArena und PDEGym. Die Datenaufteilung erfolgte nach Standardverfahren oder im Verhältnis 80/10/10 für Training/Validierung/Test, basierend auf den Trajektorien.

Im Hinblick auf die Trainingsumgebung durchlief das Walrus-Modell etwa 400.000 Vortrainingsschritte mit jeweils rund 4 Millionen Beispielen in den 2D-Datensätzen und rund 2 Millionen Beispielen in den 3D-Datensätzen. Der AdamW-Optimierer und eine entsprechende Lernratenstrategie wurden eingesetzt, um effizientes Lernen auf hochdimensionalen, multitaskingfähigen Daten zu ermöglichen. Als primäre Bewertungsmetrik diente der VRMSE (Standardized Root Mean Square Error), der eine einheitliche Bewertung über verschiedene Datensätze und Aufgaben hinweg erlaubt.

Diese äußerst vielfältigen Trainingsdaten und die gewählte Strategie ermöglichen es Walrus, während der Vortrainingsphase reichhaltige physikalische Eigenschaften zu erfassen und die Grundlage für die domänenübergreifende Generalisierung für nachfolgende Aufgaben zu schaffen.

Transformatorarchitektur basierend auf raumzeitlicher Faktorisierung

Das Walrus-Modell verwendet eine raumzeitlich faktorisierte Transformerarchitektur. Bei der Verarbeitung raumzeitlich strukturierter Tensordaten führt es Aufmerksamkeitsoperationen sowohl entlang der räumlichen als auch der zeitlichen Dimension durch, um eine effiziente Modellierung zu erreichen. Der Prozess ist in der folgenden Abbildung dargestellt:

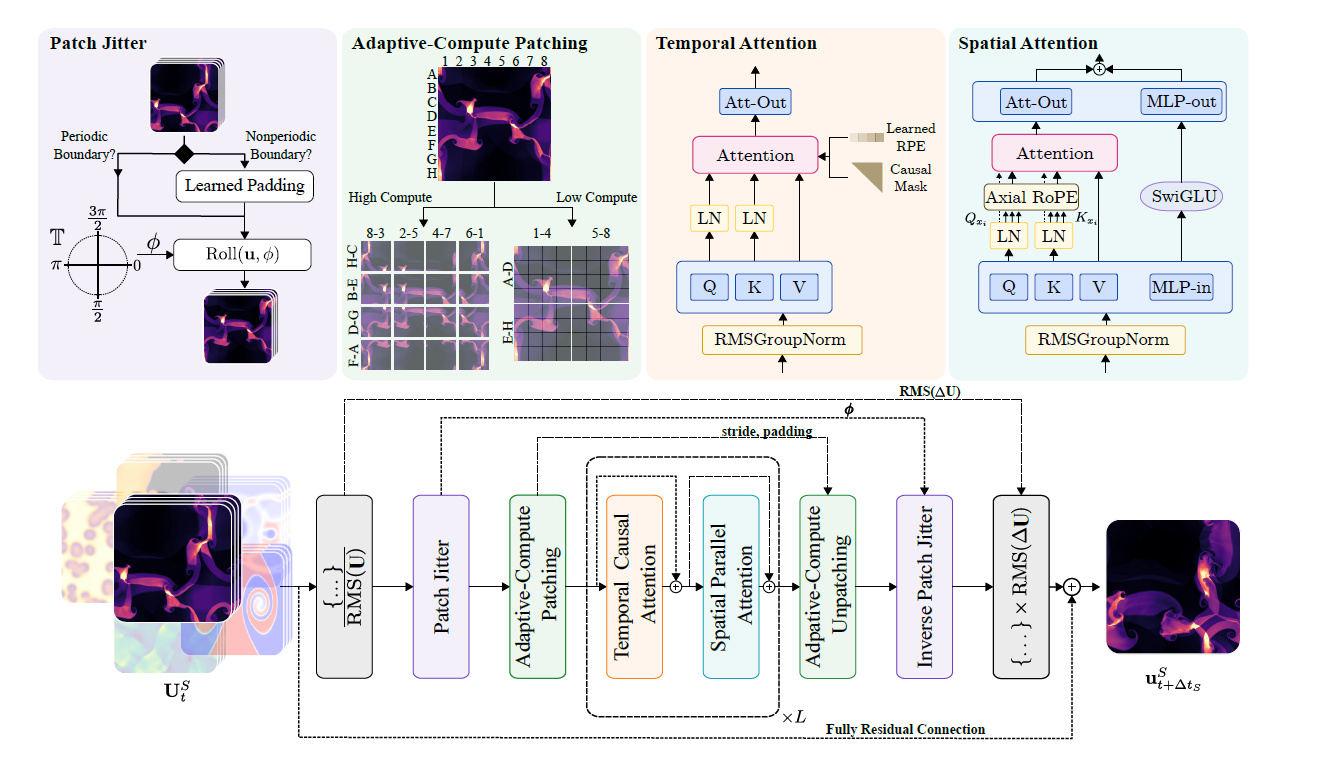
* Weltraumverarbeitung:Wir verwenden die von Wang vorgeschlagene parallele Aufmerksamkeit und kombinieren sie mit Axial RoPE zur Positionskodierung.

* Zeitleistenverarbeitung:Wir verwenden kausale Aufmerksamkeit in Kombination mit relativer Positionskodierung im T5-Stil. Die QK-Normalisierung wird sowohl im räumlichen als auch im zeitlichen Modul angewendet, um die Stabilität des Trainings zu verbessern.

* Rechenadaptive Komprimierung:In den Encoder- und Decodermodulen wird Convolutional Stride Modulation (CSM) verwendet, um Daten nativ in verschiedenen Auflösungen zu verarbeiten. Die flexible Auflösungsanpassung wird durch die Anpassung der Downsampling-/Upsampling-Stufen in jedem Encoder-/Decoderblock erreicht. Frühere Simulationsmodelle verwendeten häufig Encoder mit fester Kompression, die nicht flexibel genug waren, um den variierenden Auflösungsanforderungen nachgelagerter Aufgaben gerecht zu werden. CSM ermöglicht es Forschern, die Faltungsschrittweite für das Downsampling anzupassen und so eine räumliche Kompressionsstufe auszuwählen, die der jeweiligen Aufgabe entspricht.

* Gemeinsamer Encoder-Decoder:Alle physikalischen Systeme gleicher Dimension nutzen einen gemeinsamen Encoder und Decoder, um gemeinsame Merkmale zu erlernen. Zwei- und dreidimensionale Daten entsprechen jeweils zwei Encodern und zwei Decodern und werden mithilfe eines ressourcenschonenden hierarchischen MLP (hMLP) kodiert und dekodiert.

* RMS GroupNorm und asymmetrische Eingangs-/Ausgangsnormalisierung:RMSGroupNorm wird innerhalb jedes Transformer-Blocks zur Normalisierung verwendet, um die Stabilität des Trainings zu verbessern. Asymmetrische Normalisierung wird für inkrementelle Vorhersagen von Eingaben und Ausgaben eingesetzt, um die numerische Stabilität in verschiedenen Szenarien zu gewährleisten.

* Patch-Jittering:Durch zufälliges Verschieben der Eingangsdaten und deren anschließende umgekehrte Verarbeitung am Ausgang wird die Ansammlung von Hochfrequenzartefakten reduziert, was die Langzeitstabilität der Vorhersage deutlich verbessert, insbesondere bei Architekturen vom ViT-Typ.

* Hocheffizientes Multitasking-Training:Hierarchisches Sampling und eine normalisierte Verlustfunktion werden eingesetzt, um sicherzustellen, dass Vorhersagen schnell veränderlicher Felder nicht von langsam veränderlichen Feldern dominiert werden. Gleichzeitig werden Micro-Batch- und adaptive Tokenisierungsstrategien kombiniert, um das Problem der ungleichmäßigen Lastverteilung beim Training hochdimensionaler, heterogener Daten zu lösen.

* Einheitliche Darstellung von zwei- und dreidimensionalen Repräsentationen:Durch Hinzufügen einer einzigen Dimension zu zweidimensionalen Daten und deren Auffüllen mit Nullen, Einbetten in den dreidimensionalen Raum und anschließende Verwendung von Symmetrieverbesserung (Rotation, Spiegelung) zur diversifizierten Verstärkung wird eine dimensionsübergreifende Trainingsfähigkeit erreicht.

Insgesamt verarbeitet die Walrus-Architektur nicht nur effizient Tensordaten sowohl in räumlicher als auch in zeitlicher Dimension, sondern bewältigt auch die Herausforderungen von Multi-Task- und Multi-Physical-Szenarien durch diverse Strategien und effizientes verteiltes Training.

Walrus weist bei zahlreichen nachgelagerten Aufgaben in 2D und 3D deutliche Vorteile auf.

Um die Leistungsfähigkeit von Walrus als Basismodell und seine Leistungsfähigkeit bei nachgelagerten Aufgaben zu überprüfen, entwarfen die Forscher eine Reihe von Experimenten:

① Leistung der nachgelagerten Aufgaben

Im Vergleich zu bestehenden Basismodellen wie MPP-AViT-L, Poseidon-L und DPOT-H reduziert Walrus den durchschnittlichen VRMSE um etwa 63,61 TP3T bei der Einzelschrittvorhersage, um 56,21 TP3T bei der kurzfristigen Trajektorienvorhersage und um 48,31 TP3T bei der mittelfristigen Trajektorienvorhersage, wie in der folgenden Abbildung dargestellt:

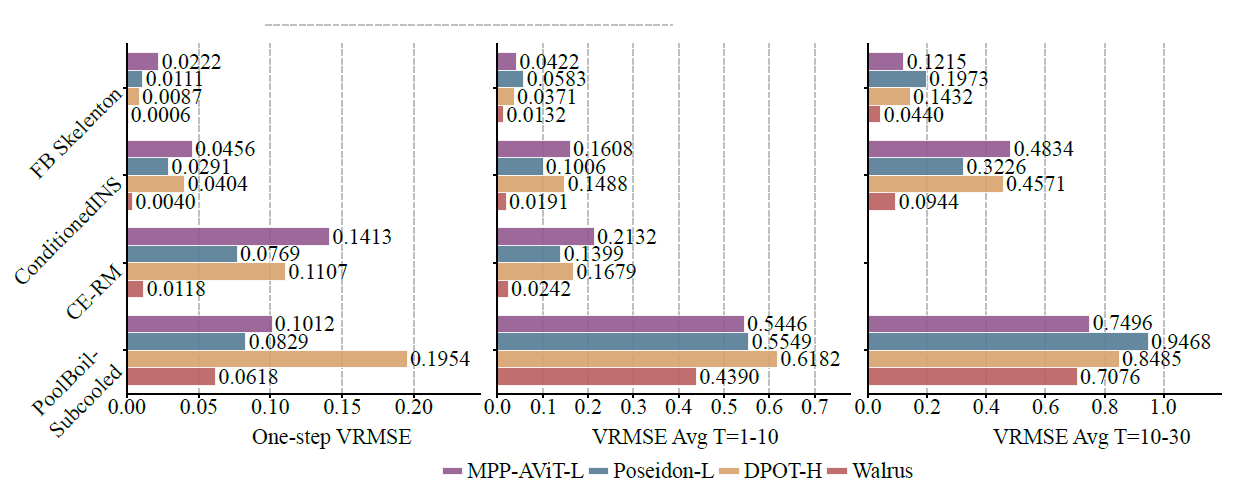
In nicht-chaotischen Systemen sorgt die geringe Artefakterzeugung durch Patch-Jittering für eine stabile Langzeitvorhersageleistung des Modells; in stärker stochastischen Systemen (wie Pool-BoilSubcool in BubbleML) ist Walrus zwar anfänglich führend, sein Vorteil bei der langfristigen rollierenden Vorhersage wird jedoch geschwächt, da kurzfristige historische Informationen die Eigenschaften von Materialien und Brennern nicht vollständig widerspiegeln können.

Dreidimensionale Aufgaben sind besonders wichtig, da die meisten realen Physiksimulationen dreidimensionale Systeme darstellen. Walrus erzielt bei den PNS- (nach Neutronensternverschmelzung) und RSG-Datensätzen (Troposphäre roter Überriesen) außergewöhnlich gute Ergebnisse, obwohl die Generierung dieser Datensätze Millionen von Kernstunden in Anspruch nimmt, wie in der folgenden Abbildung dargestellt:

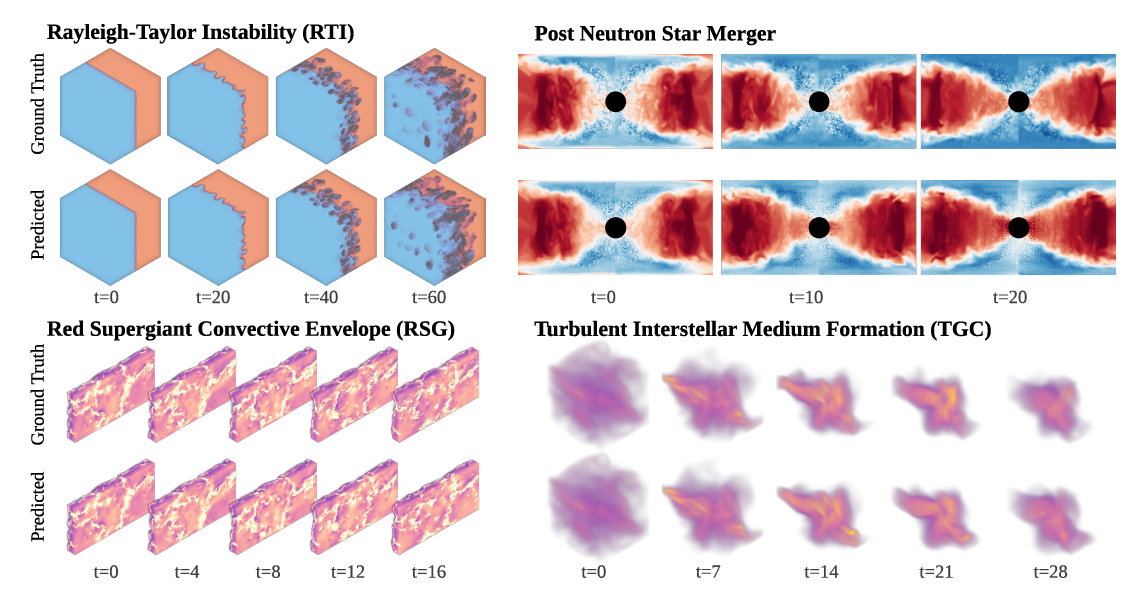
② Domänenübergreifende Fähigkeiten

Die domänenübergreifenden Fähigkeiten von Walrus wurden ebenfalls validiert; im Vergleich zur optimalen Basislinie reduzierte Walrus den durchschnittlichen Verlust bei der Einzelschrittvorhersage um 52,21 TP3T.Nach der Feinabstimmung anhand von 19 vorab trainierten Datensätzen erzielte Walrus bei 18 von 19 Aufgaben den niedrigsten Einzelschrittverlust und durchschnittliche Vorteile von 30,5% bzw. 6,3% bei mittelfristigen rollierenden Vorhersagen in 20 bzw. 20-60 Schritten, wie in der folgenden Tabelle dargestellt:

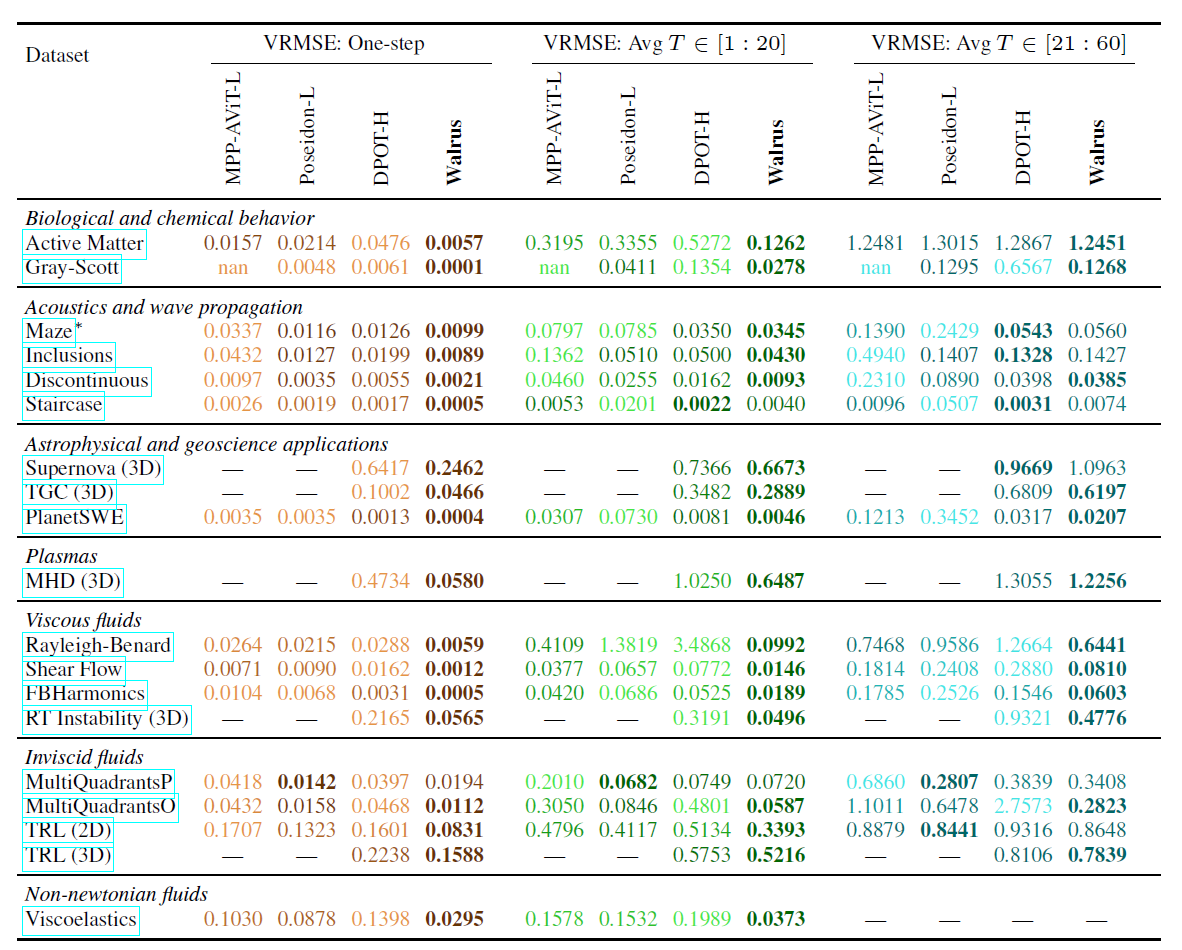
Im Vergleich dazu schneidet DPOT bei Aufgaben zur akustischen und linearen Wellenausbreitung ähnlich gut ab wie Walrus, während Poseidon bei Aufgaben zur reibungsfreien Strömung hervorragende Ergebnisse liefert. Walrus erzielt jedoch durch umfangreiches Vortraining und seine allgemeine Architektur bei den meisten Aufgaben konkurrenzfähige oder sogar bessere Ergebnisse.

③ Auswirkungen von Vorbereitungsstrategien

Ablationsstudien zeigen, dass die vielfältigen Vortrainingsstrategien von Walrus entscheidend für die nachfolgende Leistung sind. Selbst beim halb so großen Modell (HalfWalrus), das nur zweidimensionale Daten verwendet, übertrifft die Vortrainingsstrategie mit umfassenden räumlichen und zeitlichen Erweiterungen Modelle, die von Grund auf oder mit einfachen zweidimensionalen Vortrainingsstrategien trainiert wurden, bei völlig unbekannten neuen Aufgaben deutlich.

Bei Aufgaben zur kognitiven Leistungsfähigkeit in 3D-Umgebungen erzielt HalfWalrus selbst mit sehr wenigen Daten eine leichte Verbesserung, sogar ohne vorheriges Training mit 3D-Daten. Das vollständige Walrus-Modell hingegen, das mit 3D-Daten vortrainiert wurde, hat einen deutlichen Vorteil erzielt, was die Bedeutung multidimensionaler und vielfältiger Daten unterstreicht.

Polymathic AI beschleunigt die Implementierung interdisziplinärer Anwendungen künstlicher Intelligenz.

Im Bereich des wissenschaftlichen Rechnens und der technischen Modellierung löst das Potenzial von Basismodellen einen Paradigmenwechsel aus. Polymathic AI ist ein bemerkenswertes Open-Source-Forschungsprojekt, dessen Hauptziel die Entwicklung universeller Basismodelle für wissenschaftliche Daten ist, um die Implementierung interdisziplinärer Anwendungen künstlicher Intelligenz zu beschleunigen.

Im Gegensatz zu universellen großen Modellen für Aufgaben im Bereich der natürlichen Sprachverarbeitung oder Bildverarbeitung konzentriert sich Polymathic AI auf typische wissenschaftliche Rechenprobleme wie kontinuierliche dynamische Systeme, physikalische Feldsimulationen und die Modellierung von Ingenieursystemen.Die Kernidee besteht darin, ein einheitliches Modell anhand umfangreicher, multiphysikalischer und multiskalarer Daten zu trainieren, wodurch es über domänenübergreifende Transferfähigkeiten verfügt und somit die Kosten für den Aufbau eines Modells von Grund auf für jedes wissenschaftliche Problem reduziert werden – diese „domänenübergreifende Generalisierungsfähigkeit“ gilt als ein wichtiger Durchbruch in der wissenschaftlichen KI.

Polymathic AI vereint Berichten zufolge ein Team aus reinen Machine-Learning-Forschern und Fachwissenschaftlern, wird von einem wissenschaftlichen Beirat aus weltweit führenden Experten beraten und von Yann LeCun, dem Turing-Preisträger und wissenschaftlichen Leiter von Meta, unterstützt. Zudem erhält das Projekt Unterstützung von mehreren renommierten Wissenschaftlern, darunter Miles Cranmer, Assistenzprofessor für KI und Astronomie/Physik an der Universität Cambridge. Ziel ist die Entwicklung grundlegender Modelle für wissenschaftliche Daten und die Anwendung interdisziplinärer Konzepte zur Lösung branchenspezifischer Herausforderungen im Bereich KI für die Wissenschaft.

Im Jahr 2025 präsentierten Mitglieder der Polymathic AI Collaboration zwei neue KI-Modelle, die mit realen wissenschaftlichen Datensätzen trainiert wurden und für Probleme in der Astronomie und der Simulation fluidähnlicher Systeme entwickelt wurden. Eines davon war das bereits erwähnte Walrus, das andere AION-1 (Astronomical Omni-modal Network), die erste umfassende multimodale Basismodellfamilie für die Astronomie. AION-1 integriert und modelliert heterogene Beobachtungsinformationen wie Bilder, Spektren und Sternkatalogdaten mithilfe eines einheitlichen, auf der frühen Fusion basierenden Backbone-Netzwerks. Es erzielt nicht nur in Zero-Shot-Szenarien hervorragende Ergebnisse, sondern weist auch eine lineare Detektionsgenauigkeit auf, die mit aufgabenspezifischen Modellen vergleichbar ist, und demonstriert damit überlegene Leistung in einem breiten Spektrum wissenschaftlicher Aufgaben. Selbst bei einfacher Vorwärtsdetektion erreicht es State-of-the-Art-Niveau (SOTA) und übertrifft überwachte Baselines in Szenarien mit wenigen Daten deutlich.
Titel des Papiers:AION-1: Omnimodales Fundamentmodell für astronomische Wissenschaften
Papieradresse:https://arxiv.org/abs/2510.17960

Insgesamt stellt Polymathic AI eine wegweisende Erforschung des aufkommenden technologischen Paradigmas der „Basismodelle wissenschaftlicher KI“ dar. Seine langfristige Bedeutung liegt nicht nur in der Leistungsverbesserung, sondern auch im Aufbau einer allgemeinen Rechengrundlage für den interdisziplinären Wissenstransfer und damit in der Schaffung der Basis für „KI für die Wissenschaft“, um von Anwendungen auf Werkzeugebene zu Fähigkeiten auf Infrastrukturebene überzugehen.

Quellen:
1.https://arxiv.org/abs/2511.15684
2.https://www.thepaper.cn/newsDetail_forward_32173693
3.https://polymathic-ai.org
4.https://arxiv.org/abs/2510.17960
5.https://www.163.com/dy/article/KGMRMMQM055676SU.html