Dans les domaines du calcul scientifique et de la simulation en ingénierie, la prédiction efficace et précise de l'évolution des systèmes physiques complexes a toujours constitué un défi majeur pour la recherche et l'industrie. Bien que les méthodes numériques traditionnelles puissent théoriquement résoudre la plupart des équations physiques, elles s'avèrent très gourmandes en ressources de calcul lorsqu'il s'agit de scénarios multiphysiques de grande dimension ou de conditions aux limites non uniformes, et manquent d'adaptabilité au traitement multitâche à grande échelle.Parallèlement, les avancées réalisées dans le domaine de l'apprentissage profond appliqué au traitement automatique du langage naturel et à la vision par ordinateur ont incité les chercheurs à explorer la possibilité d'appliquer des « modèles de base » dans des simulations physiques.

Cependant, les systèmes physiques évoluent souvent à différentes échelles temporelles et spatiales, tandis que la plupart des modèles d'apprentissage sont généralement entraînés uniquement sur des dynamiques à court terme. Une fois utilisés pour des prédictions à long terme, les erreurs s'accumulent dans les systèmes complexes, ce qui entraîne une instabilité du modèle.De plus, les différentes échelles et l'hétérogénéité des systèmes impliquent que les tâches en aval ont des exigences variables en matière de résolution de modélisation, de dimensionnalité et de types de champs physiques, ce qui représente un défi majeur pour les architectures d'apprentissage modernes qui privilégient des formats d'entrée fixes. Par conséquent, la plupart des modèles fondamentaux utilisés à ce jour pour la simulation restent limités à des scénarios de données relativement homogènes, par exemple en ne traitant que des problèmes bidimensionnels plutôt que des situations tridimensionnelles plus réalistes.

Dans ce contexte, une équipe de recherche de la Polymathic AI Collaboration a introduit une série de nouvelles méthodes pour relever les défis susmentionnés, notamment : le jittering de patchs, des stratégies d'entraînement distribuées à charge équilibrée pour les scénarios 2D-3D et des mécanismes de tokenisation à calcul adaptatif.Sur cette base, l'équipe de recherche a proposé un modèle fondamental appelé Walrus, qui comporte 1,3 milliard de paramètres, utilise Transformer comme architecture de base et est principalement orienté vers la dynamique des milieux continus de type fluide. Lors de sa phase de pré-entraînement, Walrus couvre 19 scénarios physiques très diversifiés, englobant de multiples domaines tels que l'astrophysique, les sciences de la Terre, la rhéologie, la physique des plasmas, l'acoustique et la dynamique des fluides classique. Les résultats expérimentaux démontrent que Walrus surpasse les modèles de référence précédents, tant pour les prédictions à court terme qu'à long terme des tâches en aval, et présente une meilleure capacité de généralisation sur l'ensemble des données de pré-entraînement.

Les résultats de recherche associés, intitulés « Walrus : un modèle de base interdomaines pour la dynamique continue », ont été publiés en prépublication sur arXiv.

Points saillants de la recherche :

Walrus possède une échelle de paramètres de modèle de 1,3 milliard, des techniques de stabilisation innovantes et la capacité d'adapter le calcul à la complexité du problème ;

* Il aborde plusieurs limitations des modèles fondamentaux actuels pour la dynamique continue, telles que l'adaptation des coûts, la stabilité et l'apprentissage efficace sur des données d'entraînement très hétérogènes à la résolution native ;

* Walrus est à ce jour le modèle de base le plus précis pour la simulation de continuum, atteignant des résultats de pointe sur 56 des 65 indicateurs suivis dans 26 tâches de simulation de continuum uniques issues de multiples domaines scientifiques et sur plusieurs échelles de temps.

Adresse du document :https://arxiv.org/abs/2511.15684
Suivez notre compte WeChat officiel et répondez « simulation média » en arrière-plan pour obtenir le PDF complet.

Autres articles sur les frontières de l'IA :
https://hyper.ai/papers

Construction d'ensembles de données hétérogènes, multidimensionnels et de haute qualité

Le succès de Walrus repose indissociable de la diversité et de la haute qualité des données. L'équipe de recherche a utilisé un jeu de données hybride issu de Well et FlowBench pour le pré-entraînement. Le jeu de données Well fournit une grande quantité de données haute résolution provenant de problèmes scientifiques réels, tandis que FlowBench introduit des obstacles géométriquement complexes dans des scénarios de fluides standard, offrant ainsi au modèle la possibilité d'apprendre des régimes d'écoulement complexes.

L'équipe de recherche a utilisé un total de 19 ensembles de données, couvrant 63 variables d'état, incluant différentes équations, conditions aux limites et paramètres de paramétrisation physique.Les données sont dimensionnées en deux et trois dimensions afin de garantir la capacité de généralisation du modèle à différentes dimensions spatiales. Pour vérifier sa transférabilité, l'équipe de recherche a affiné le modèle à l'aide d'une partie des jeux de données réservés, incluant les données de Well, FlowBench, PDEBench, PDEArena et PDEGym, après un pré-entraînement. La répartition des données a suivi des stratégies de partitionnement standard ou a été divisée selon un ratio 80/10/10 pour l'entraînement, la validation et les tests, en fonction des trajectoires.

Concernant les paramètres d'entraînement, le modèle Walrus a subi environ 400 000 étapes de pré-entraînement, avec environ 4 millions d'échantillons dans chaque ensemble de données 2D et environ 2 millions d'échantillons dans chaque ensemble de données 3D. L'optimiseur AdamW et une stratégie de planification du taux d'apprentissage ont été utilisés pour un apprentissage efficace sur des données multidimensionnelles et multitâches. La principale métrique d'évaluation utilisée était l'erreur quadratique moyenne normalisée (VRMSE), permettant une évaluation unifiée pour l'ensemble des ensembles de données et des tâches.

Ces données et cette stratégie d'entraînement très diversifiées permettent à Walrus de capturer de riches propriétés physiques pendant la phase de pré-entraînement et de jeter les bases d'une généralisation interdomaines pour les tâches en aval.

Architecture de transformateur basée sur la factorisation spatio-temporelle

Le modèle Walrus utilise une architecture de transformateur factorisée spatio-temporelle. Lors du traitement de données structurées en tenseurs spatio-temporels, il effectue des opérations d'attention sur les dimensions spatiale et temporelle afin d'obtenir une modélisation efficace. Ce processus est illustré dans la figure ci-dessous :

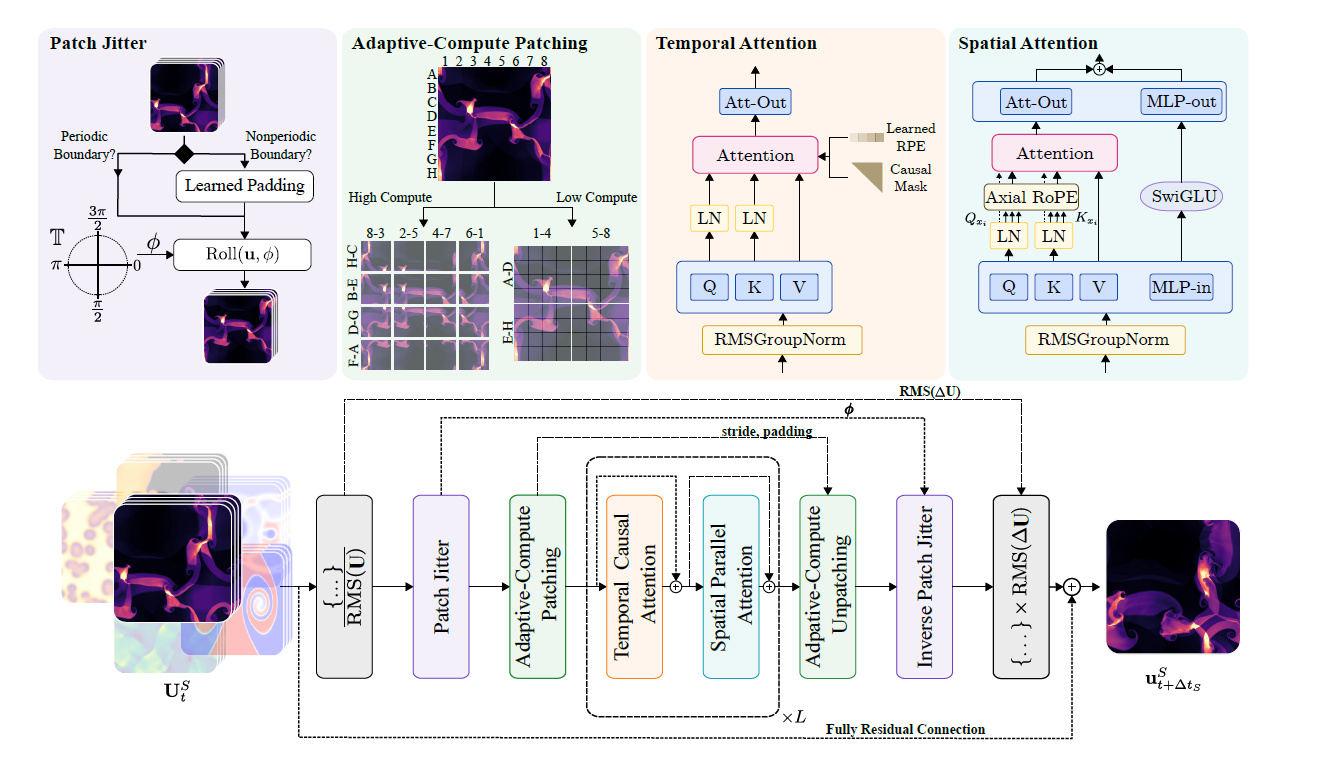
* Traitement spatial :Nous utilisons l'attention parallèle proposée par Wang et la combinons avec Axial RoPE pour l'encodage de position.

* Traitement chronologique :Nous utilisons l'attention causale combinée à un codage de position relative de type T5. La normalisation QK est appliquée aux modules spatiaux et temporels afin d'améliorer la stabilité de l'entraînement.

* Compression adaptative au calcul :Dans les modules d'encodage et de décodage, la modulation du pas de convolution (CSM) est utilisée pour traiter nativement les données à différentes résolutions. La gestion flexible de la résolution est assurée par l'ajustement des niveaux de sous-échantillonnage/sur-échantillonnage dans chaque bloc d'encodage/décodage. Les modèles de simulation précédents utilisaient souvent des encodeurs à compression fixe, insuffisamment flexibles pour répondre aux exigences de résolution variables des tâches en aval. La CSM permet aux chercheurs d'ajuster le pas de convolution pour le sous-échantillonnage, sélectionnant ainsi un niveau de compression spatiale adapté à la tâche.

* Encodeur-décodeur partagé :Tous les systèmes physiques de même dimension partagent un seul encodeur et un seul décodeur pour apprendre les caractéristiques communes. Les données bidimensionnelles et tridimensionnelles correspondent respectivement à deux encodeurs et deux décodeurs, et sont encodées et décodées à l'aide d'un MLP hiérarchique léger (hMLP).

* Normalisation RMS GroupNorm et normalisation asymétrique des entrées/sorties :La normalisation RMSGroupNorm est utilisée au sein de chaque bloc Transformer afin d'améliorer la stabilité de l'apprentissage. Une normalisation asymétrique est employée pour les prédictions incrémentales des entrées et des sorties afin de garantir la stabilité numérique dans différents scénarios.

* Tremblements du patch :En décalant aléatoirement les données d'entrée puis en les traitant en sens inverse à la sortie, l'accumulation d'artefacts à haute fréquence est réduite, améliorant considérablement la stabilité des prédictions à long terme, notamment dans les architectures de type ViT.

* Formation multitâche à haute efficacité :L'échantillonnage hiérarchique et la fonction de perte normalisée sont utilisés pour éviter que les prédictions concernant des champs à évolution rapide ne soient biaisées par celles concernant des champs à évolution lente. Parallèlement, le traitement par micro-lots et la tokenisation adaptative sont combinés pour pallier le problème de la charge inégale lors de l'entraînement sur des données hétérogènes de grande dimension.

* Représentation unifiée des représentations bidimensionnelles et tridimensionnelles :En ajoutant une seule dimension à des données bidimensionnelles et en les remplissant de zéros, en les intégrant dans un espace tridimensionnel, puis en utilisant l'amélioration de la symétrie (rotation, réflexion) pour une amplification diversifiée, une capacité d'entraînement interdimensionnelle est obtenue.

Globalement, l'architecture Walrus traite non seulement efficacement les données tensorielles dans les dimensions spatiales et temporelles, mais relève également les défis des scénarios multitâches et multiphysiques grâce à des stratégies diverses et à un apprentissage distribué efficace.

Walrus présente des avantages significatifs dans de multiples tâches en aval 2D et 3D.

Afin de vérifier les performances de Walrus en tant que modèle de base et ses performances dans les tâches en aval, les chercheurs ont conçu une série d'expériences :

① Performances des tâches en aval

Comparé aux modèles de référence existants tels que MPP-AViT-L, Poseidon-L et DPOT-H, Walrus réduit l'erreur quadratique moyenne (VRMSE) d'environ 63,61 TP3T dans la prédiction à une étape unique, de 56,21 TP3T dans la prédiction de trajectoire à court terme et de 48,31 TP3T dans la prédiction de trajectoire à moyen terme, comme le montre la figure ci-dessous :

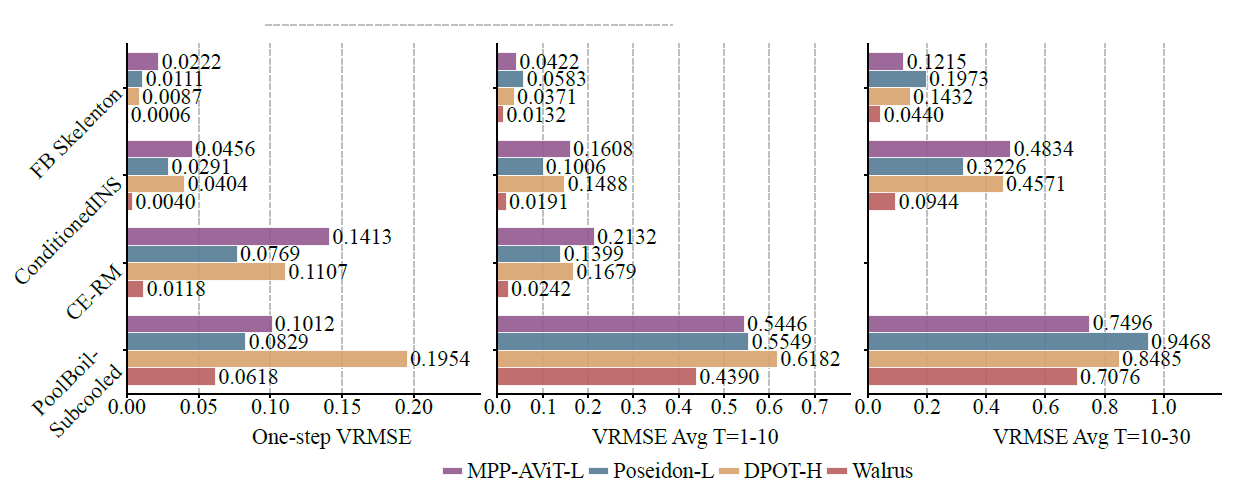
Dans les systèmes non chaotiques, la faible génération d'artefacts provoquée par la variation aléatoire des patchs stabilise les performances de prédiction à long terme du modèle ; dans les systèmes plus stochastiques (tels que Pool-BoilSubcool dans BubbleML), bien que Walrus prenne initialement l'avantage, son avantage en matière de prédiction glissante à long terme s'affaiblit car les informations historiques à court terme ne peuvent pas refléter pleinement les caractéristiques des matériaux et des brûleurs.

Les tâches tridimensionnelles sont particulièrement importantes car la plupart des simulations physiques réelles concernent des systèmes tridimensionnels. Walrus obtient des résultats exceptionnels sur les jeux de données PNS (post-fusion d'étoiles à neutrons) et RSG (troposphère de supergéante rouge), même si leur génération nécessite des millions d'heures de calcul, comme le montre la figure ci-dessous :

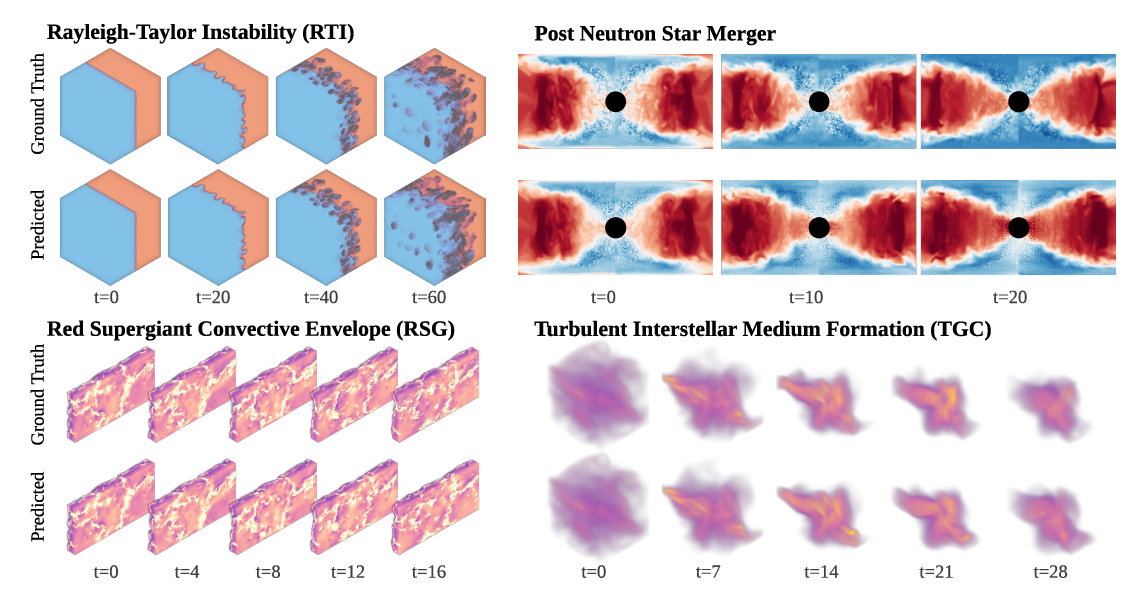
② Capacités interdomaines

Les capacités interdomaines de Walrus ont également été validées ; par rapport à la référence optimale, Walrus a réduit la perte moyenne de 52,21 TP3T dans la prédiction en une seule étape.Après un réglage fin sur 19 ensembles de données pré-entraînés, Walrus a obtenu la perte la plus faible en une seule étape sur 18/19 tâches, et des avantages moyens de 30,5% et 6,3% dans les prédictions glissantes à moyen terme à 20 et 20-60 étapes, respectivement, comme indiqué dans le tableau ci-dessous :

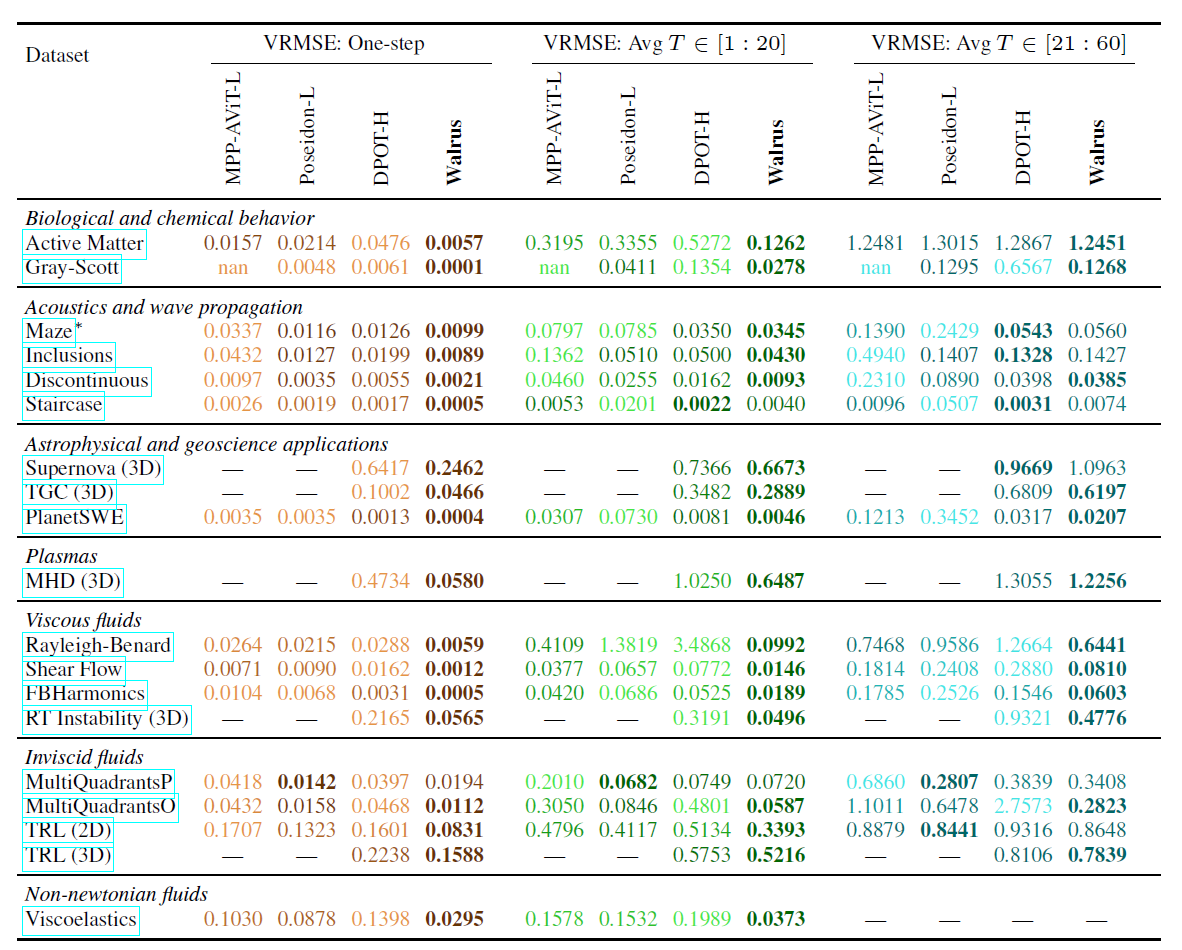
En comparaison, DPOT offre des performances proches de celles de Walrus pour les tâches de propagation d'ondes acoustiques et linéaires, tandis que Poseidon excelle dans les tâches d'écoulement non visqueux. Cependant, grâce à un pré-entraînement poussé et à une architecture générale, Walrus obtient des résultats compétitifs, voire supérieurs, sur la plupart des tâches.

③ Impact des stratégies de pré-formation

Des expériences d'ablation montrent que les diverses stratégies de pré-entraînement de Walrus sont cruciales pour ses performances ultérieures. Même sur le modèle réduit (HalfWalrus) utilisant uniquement des données bidimensionnelles, la stratégie de pré-entraînement avec des augmentations spatiales et temporelles complètes surpasse significativement les modèles entraînés à partir de zéro ou avec de simples stratégies de pré-entraînement bidimensionnelles sur des tâches totalement inédites.

Dans les tâches 3D du SNC, HalfWalrus peut obtenir une légère amélioration même avec très peu de données, et ce, sans avoir préalablement vu de données 3D. Le modèle Walrus complet, grâce à un pré-entraînement avec des données 3D, présente un avantage significatif, soulignant l'importance de données multidimensionnelles et diversifiées.

L'IA polymathe accélère la mise en œuvre d'applications d'intelligence artificielle interdisciplinaires.

Dans les domaines du calcul scientifique et de la modélisation en ingénierie, le potentiel des modèles fondamentaux engendre un changement de paradigme majeur. Polymathic AI est un projet de recherche open source remarquable dont l'objectif principal est de construire des modèles fondamentaux génériques pour les données scientifiques afin d'accélérer le déploiement d'applications d'intelligence artificielle interdisciplinaires.

Contrairement aux grands modèles à usage général destinés aux tâches de traitement du langage naturel ou de vision, Polymathic AI se concentre sur les problèmes typiques de calcul scientifique tels que les systèmes dynamiques continus, la simulation de champs physiques et la modélisation de systèmes d'ingénierie.Son idée centrale est d'entraîner un modèle unifié à travers des données à grande échelle, multiphysiques et multi-échelles, lui permettant d'avoir des capacités de transfert inter-domaines, réduisant ainsi le coût de la construction d'un modèle à partir de zéro pour chaque problème scientifique - cette « capacité de généralisation inter-domaines » est considérée comme une avancée majeure dans l'IA scientifique.

Polymathic AI réunit une équipe de chercheurs en apprentissage automatique et de scientifiques spécialisés dans différents domaines, bénéficie des conseils d'un comité consultatif scientifique composé d'experts de renommée mondiale et est conseillé par Yann LeCun, lauréat du prix Turing et directeur scientifique de Meta. L'entreprise reçoit également le soutien de plusieurs personnalités du monde universitaire, dont Miles Cranmer, professeur adjoint d'IA et d'astronomie/physique à l'université de Cambridge. Son objectif est de se concentrer sur le développement de modèles fondamentaux pour les données scientifiques et sur l'utilisation de concepts interdisciplinaires partagés pour relever les défis industriels liés à l'IA au service de la science.

En 2025, les membres de la collaboration Polymathic AI ont présenté deux nouveaux modèles d'intelligence artificielle, entraînés sur des jeux de données scientifiques réels et conçus pour résoudre des problèmes en astronomie et en mécanique des fluides. L'un d'eux était Walrus, mentionné précédemment, et l'autre AION-1 (Astronomical Omni-modal Network), la première famille de modèles multimodaux fondamentaux à grande échelle pour l'astronomie. AION-1 intègre et modélise des informations observationnelles hétérogènes, telles que des images, des spectres et des données de catalogues d'étoiles, grâce à un réseau dorsal de fusion précoce unifié. Il offre non seulement des performances exceptionnelles dans des scénarios sans données d'entraînement, mais aussi une précision de détection linéaire comparable à celle des modèles dédiés, démontrant ainsi des performances supérieures pour un large éventail de tâches scientifiques. Même avec une simple détection directe, ses performances atteignent l'état de l'art et il surpasse significativement les modèles de référence supervisés dans des scénarios avec peu de données.
Titre de l'article :AION-1 : Modèle fondamental omnimodal pour les sciences astronomiques
Adresse du document :https://arxiv.org/abs/2510.17960

Dans l'ensemble, Polymathic AI représente une exploration de pointe du paradigme technologique émergent des « modèles de base de l'IA scientifique ». Son importance à long terme réside non seulement dans l'amélioration des performances, mais aussi dans la construction d'une base informatique générale pour le transfert de connaissances interdisciplinaires, jetant ainsi les bases permettant à « l'IA pour la science » de passer d'applications au niveau des outils à des capacités au niveau de l'infrastructure.

Références :
1.https://arxiv.org/abs/2511.15684
2.https://www.thepaper.cn/newsDetail_forward_32173693
3.https://polymathic-ai.org
4.https://arxiv.org/abs/2510.17960
5.https://www.163.com/dy/article/KGMRMMQM055676SU.html