Dans l'étude des systèmes complexes, les « réseaux » sont quasi omniprésents : des réseaux de régulation génique et des communautés microbiennes aux réseaux de communication et de transport au sein des sociétés humaines. Cependant, la compréhension véritable des dynamiques sous-jacentes à ces réseaux multidimensionnels demeure l'un des problèmes les plus ardus du domaine.

d'une part,Le développement des capteurs, des technologies de séquençage et des infrastructures numériques a permis aux gens d'avoir accès à une quantité sans précédent de données d'observation ;d'autre part,Les modèles mathématiques explicables capables d'expliquer ces données et de révéler les mécanismes causaux font cruellement défaut. La forte dimensionnalité, la non-linéarité marquée et l'hétérogénéité structurelle impliquent que les méthodes de modélisation traditionnelles reposent soit sur des hypothèses fortes et ont une applicabilité limitée, soit se limitent à l'analyse de corrélation, sans parvenir à saisir les lois essentielles qui régissent le fonctionnement du système.

En réponse aux défis rencontrés,Le professeur Li Yong et son équipe du département de génie électronique de l'université Tsinghua ont proposé une méthode de régression symbolique neuronale, ND².Cette méthode caractérise la dynamique des systèmes en dérivant automatiquement des formules mathématiques à partir des données. Elle simplifie le problème de recherche sur les réseaux multidimensionnels en un système unidimensionnel et utilise des réseaux neuronaux pré-entraînés pour guider la découverte de formules de haute précision. Dans des études sur la transmission des maladies infectieuses sur les réseaux de mobilité humaine à différentes échelles, cette méthode a révélé une dynamique de corrélation des nœuds présentant la même distribution en loi de puissance à toutes les échelles et a mis en évidence des différences d'efficacité des interventions selon les pays.

Les recherches connexes, intitulées « Découverte de la dynamique des réseaux par régression symbolique neuronale », ont été publiées dans Nature Computational Science.

Lien vers l'article :

https://www.nature.com/articles/s43588-025-00893-8

Suivez notre compte WeChat officiel et répondez « régression symbolique neuronale » en arrière-plan pour télécharger le PDF complet.

Autres articles sur les frontières de l'IA :
https://hyper.ai/papers

Un algorithme de recherche de symboles guidé par NDformer est introduit pour parvenir à une découverte de formules efficace.

Des chercheurs ont proposé une méthode de régression symbolique neuronale (Neural Discovery of Network Dynamics, ND²), une approche d'apprentissage profond qui découvre automatiquement les formules de la dynamique des réseaux par régression symbolique. À cette fin,Les chercheurs ont conçu un ensemble d'opérateurs dynamiques de réseau.Cela transforme le problème de recherche de symboles, initialement sur des réseaux de grande dimension, en un problème unidimensionnel équivalent ; simultanément...Un algorithme de recherche symbolique guidé par NDformer est introduit.Pour parvenir à une découverte de formules efficace.

Comme illustré dans la figure ci-dessous, les opérateurs de dynamique de réseau comprennent l'opérateur source φ(s), l'opérateur cible φ(t) et l'opérateur d'agrégation ρ. Ces opérateurs rendent l'expression de la formule de dynamique de réseau indépendante de la taille du réseau, comprimant ainsi l'espace de recherche qui croît initialement de manière exponentielle avec la taille du réseau en un problème unidimensionnel indépendant de la dimension.

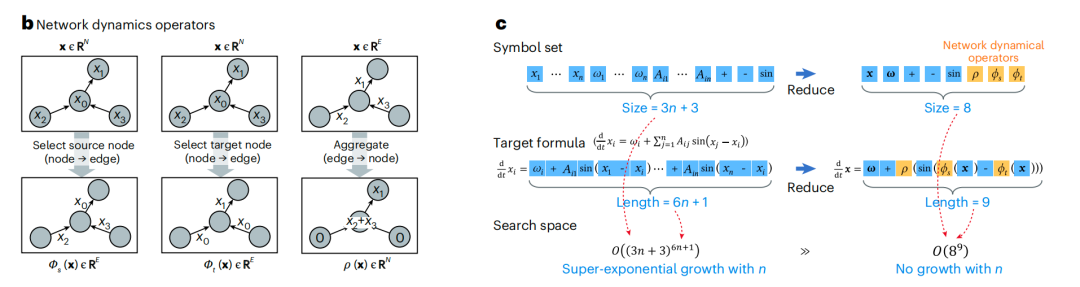
De plus, l'algorithme de recherche symbolique guidé par NDformer améliore considérablement l'efficacité et la précision de la découverte de formules en combinant les avantages des réseaux neuronaux et des méthodes de recherche symbolique.L'algorithme se compose d'un module symbolique chargé de la recherche et d'un module neuronal chargé du guidage.Comme le montre la figure ci-dessous, le module neuronal NDformer apprend à capturer les caractéristiques implicites de la dynamique sous-jacente du système et estime la distribution de probabilité de chaque symbole nécessaire à la construction de la formule ; le module de symboles MCTS sélectionne les symboles en fonction des probabilités prédites par NDformer, construisant ainsi des formules candidates.

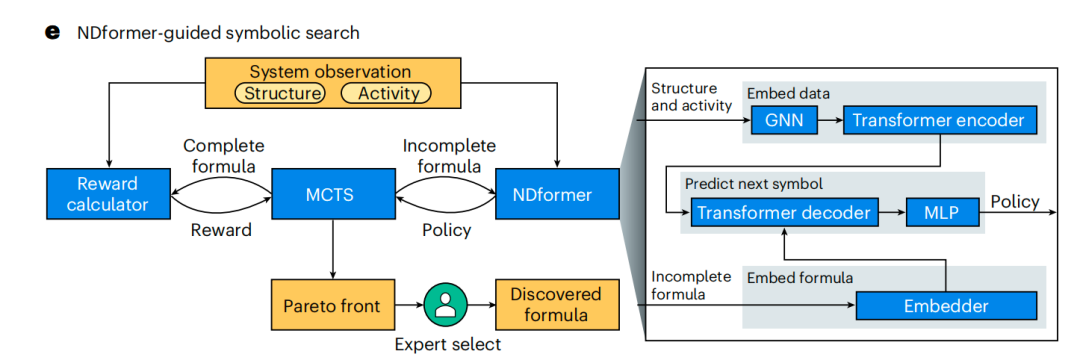
Pour chaque formule candidate, le calculateur de récompense utilise l'algorithme BFGS (Broyden–Fletcher–Goldfarb–Shanno) afin d'ajuster les coefficients inconnus (le cas échéant) aux données et attribue une récompense qui évalue de manière globale la précision et la simplicité. Les formules candidates les plus adaptées aux données et les plus courtes reçoivent des récompenses plus élevées, ce qui permet à MCTS de générer continuellement de meilleures formules candidates.

Spécifiquement,NDformer est un type de réseau neuronal qui combine les réseaux neuronaux graphiques (GNN) et les transformateurs.Utilisé pour capturer les caractéristiques dynamiques complexes des réseaux, NDformer apprend, grâce à un pré-entraînement, à prédire les signes dans la formule à partir de la structure du réseau et des données d'activité des nœuds. Il guide ensuite le module de recherche arborescente Monte Carlo (MCTS) afin d'explorer efficacement l'espace de recherche et de découvrir ainsi une formule de dynamique de réseau précise et concise.

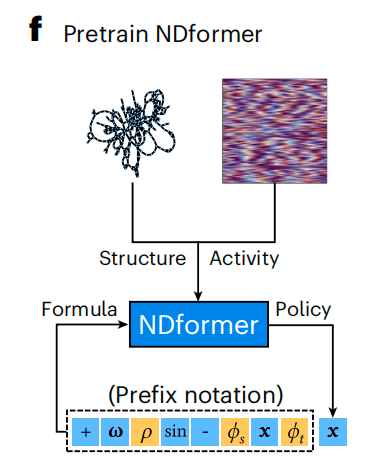
Révéler la dynamique microscopique des phénomènes d’« émergence » dans des systèmes complexes multi-échelles et multidisciplinaires.

Pour vérifier l'efficacité de la méthode de régression symbolique neuronale, l'équipe de recherche a appliqué la méthode de régression symbolique neuronale ND² à des systèmes complexes à plusieurs échelles et dans différents domaines, de l'échelle cellulaire à l'échelle urbaine, couvrant les réseaux génétiques, écologiques et sociaux, pour explorer la dynamique microscopique derrière différents systèmes complexes, comme le montre la figure ci-dessous.

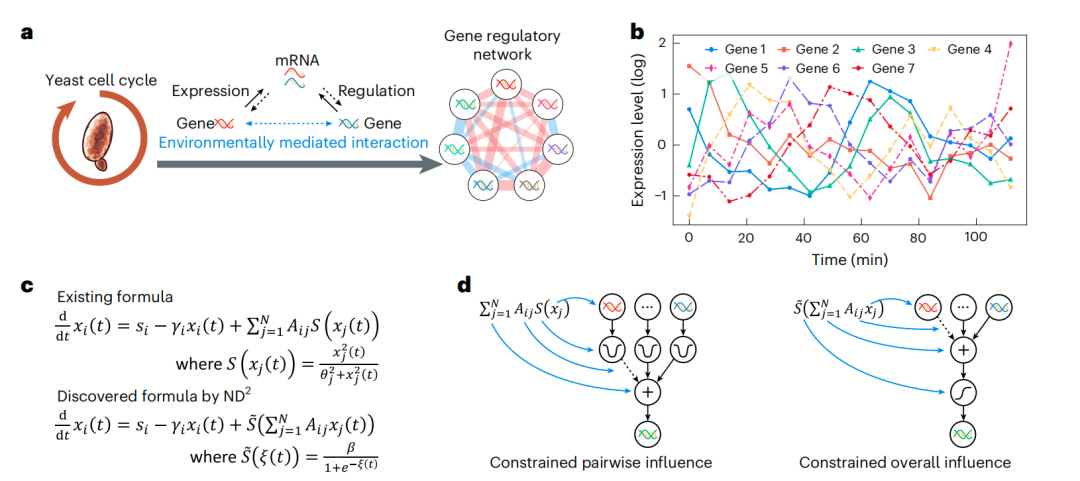
Dans les réseaux d'expression génique,La formule dynamique découverte par l'équipe de recherche améliore la précision des prédictions d'environ 60% par rapport aux formules empiriques existantes.Plus important encore, la formule découverte révèle des interactions d'ordre supérieur : la régulation mutuelle entre deux gènes n'est pas seulement influencée par les deux gènes eux-mêmes, mais aussi par un troisième gène, présentant ainsi une structure dynamique microscopique complexe.

Dans l'écosystème microbien,La formule dynamique découverte améliore la précision des prédictions d'environ 561 TP3T par rapport au modèle traditionnel de Lotka-Volterra.Elle présente également des comportements uniques qui n'ont pas encore été observés dans les modèles existants : les populations comptant un plus grand nombre d'individus sont moins affectées par les autres populations.

Parallèlement, des chercheurs ont également appliqué la méthode de régression symbolique ND² pour identifier les mécanismes de transmission des maladies infectieuses dans les systèmes urbains à différentes échelles. L'étude a sélectionné sept régions représentatives, couvrant les réseaux de transmission de l'échelle locale à l'échelle mondiale, et a permis de découvrir automatiquement les équations dynamiques de la transmission épidémique grâce à cette méthode, comme illustré dans la figure ci-dessous.

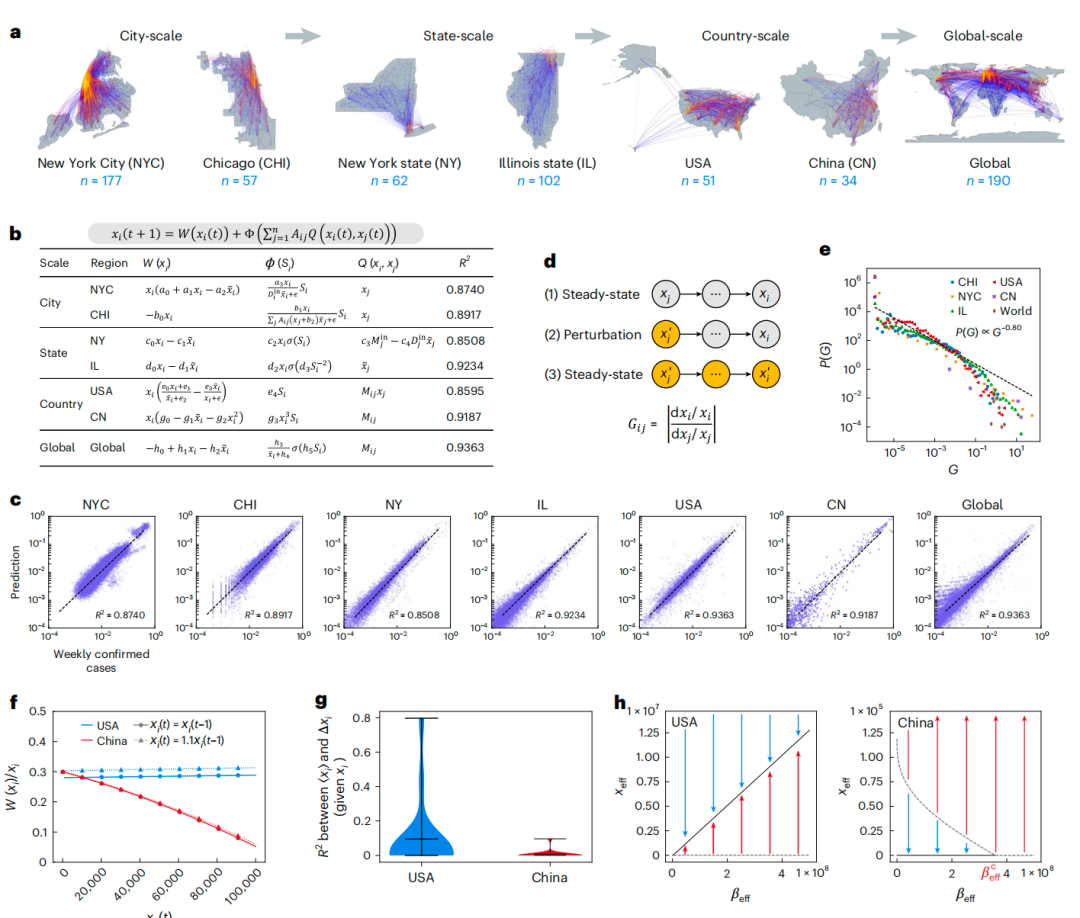
Ces équations démontrent une grande précision dans les prédictions et révèlent des différences dans les mécanismes de propagation selon les régions.Prenons l'exemple des États-Unis et de la Chine : leur dynamique d'auto-évolution présente des caractéristiques différentes. Aux États-Unis, le processus de transmission reste stable, tandis qu'en Chine, l'intensité de la transmission diminue à mesure que le nombre d'infections augmente, ce qui témoigne d'un mécanisme d'autorégulation et reflète l'efficacité des politiques de prévention et de contrôle. Concernant la dynamique des interactions interrégionales, le nombre de nouvelles infections dans chaque État américain dépend des nouveaux cas dans les autres États, ce qui indique que les déplacements interétatiques favorisent la propagation de l'épidémie. En Chine, en revanche, les liens de transmission entre les provinces sont extrêmement faibles, ce qui indique que la transmission transrégionale est strictement contrôlée. Ces différences sont parfaitement cohérentes avec les différences d'intensité des stratégies de prévention et de contrôle mises en œuvre par les deux pays.

À partir des équations dynamiques découvertes, les chercheurs ont analysé plus en détail les caractéristiques macroscopiques à l'état stationnaire du système. Les résultats montrent que la propagation de l'épidémie en Chine et aux États-Unis présente des schémas radicalement différents : en Chine, lorsque le trafic interprovincial reste inférieur à un certain seuil, le nombre d'infections peut être maîtrisé pendant une longue période ; une fois ce seuil dépassé, le nombre d'infections explose, présentant un comportement critique typique ; tandis qu'aux États-Unis, le nombre moyen d'infections augmente linéairement avec le trafic interétatique, ce qui indique que la régulation du trafic a un impact relativement faible sur la transmission globale. Cette étude révèle non seulement l'origine dynamique des différences observées dans la prévention et le contrôle de l'épidémie entre les deux pays,Elle démontre également le vaste potentiel de la méthode de régression symbolique neuronale pour extraire les mécanismes microscopiques à l'origine de l'« émergence » à différentes échelles des systèmes complexes.

Grâce à une validation multidisciplinaire et à différentes échelles, l'équipe de recherche a non seulement prouvé l'efficacité de la méthode de régression symbolique neuronale, mais a également démontré son potentiel pour révéler la dynamique microscopique des systèmes complexes et découvrir de nouvelles connaissances scientifiques, fournissant ainsi de nouveaux outils et de nouvelles idées pour la recherche scientifique fondamentale et la découverte scientifique.

À propos de l'équipe

Le Centre pour la science et l'informatique urbaines (FIB LAB) du département de génie électronique de l'université Tsinghua mène des recherches de pointe en intelligence artificielle et en science des données. Ses travaux portent sur les innovations technologiques majeures dans les modèles fondamentaux, la recherche en IA et la modélisation du monde, explorant l'utilisation de l'apprentissage automatique pour modéliser, générer, simuler et contrôler des systèmes complexes à différentes échelles. Les objets de recherche englobent les robots, les drones et le comportement humain en environnements intérieurs et extérieurs, établissant des liens entre l'espace physique, le monde numérique et les systèmes sociaux. Le laboratoire se concentre sur des applications telles que l'intelligence incarnée, la science urbaine et l'informatique sociale, en privilégiant l'intégration multidisciplinaire et les capacités de modélisation de systèmes à grande échelle afin de répondre aux besoins importants des domaines connexes.