La Nouvelle Approche De l'IA De Google DeepMind Pour Le Prix Du Millénaire Vise À Découvrir De Nouvelles Singularités Instables Dans Trois Équations fluides.

Dès la fin du mois de mai de cette année, le mathématicien Javier Gómez Serrano a révélé dans une interview qu'il travaillait avec Google DeepMind pour« Essayer de résoudre l'une des énigmes les plus insolubles connues de l'humanité - les équations de Navier-Stokes - aussi rapidement que possible. »L'équation est l'un des sept problèmes du prix du millénaire décernés par le Clay Mathematics Institute, avec un prix d'un million de dollars pour le résolveur.

Selon certaines informations, le projet baptisé « Opération Navier-Stokes », lancé par Javier Gómez Serrano et d'autres, dure depuis trois ans et est mené par une équipe de 20 personnes, toujours dans le plus grand secret. Cependant, Demis Hassabis, directeur de Google DeepMind, a également révélé lors d'une interview en janvier dernier queIl a déclaré être « sur le point de résoudre un problème lié au Prix du Millénaire », sans toutefois préciser lequel. « Nous connaîtrons la réponse d'ici un an ou un an et demi. »

Or, cette opération mystérieuse semble avoir été progressivement dévoilée.

Google DeepMind, en collaboration avec des chercheurs de l'Université de New York, de l'Université de Stanford, de l'Université Brown et d'autres institutions, a développé un cadre d'apprentissage automatique et un optimiseur Gauss-Newton de haute précision.De nouvelles singularités instables ont été découvertes systématiquement pour la première fois dans trois équations de fluides différentes.Une formule asymptotique empirique concise est révélée, reliant le taux d’explosion à l’ordre d’instabilité.

Les résultats expérimentaux montrent queLa méthode a atteint une précision nettement supérieure à celle des travaux existants sur toutes les solutions trouvées.Pour des solutions CCF spécifiques, les résultats sont même proches de la limite de la machine à virgule flottante double précision, limitée uniquement par l'erreur d'arrondi du matériel GPU, offrant un nouveau paradigme de recherche pour explorer le paysage complexe des équations aux dérivées partielles non linéaires (EDP) et ouvrant de nouvelles voies pour surmonter les problèmes de longue date de la physique mathématique.

La recherche connexe s'intitule « Découverte de singularités instables » et a été publiée sous forme de pré-impression sur arXiv.

Adresse du document :
https://go.hyper.ai/iGh6t
Suivez le compte officiel et répondez « Singularité instable » pour télécharger l'article complet.

Découvrir et analyser les structures à deux étages et trouver des singularités instables

Si l'on considère l'histoire de l'exploration humaine des lois de la nature, la mécanique des fluides a toujours été l'un des domaines les plus complexes et les plus exigeants. Pendant des siècles, les mathématiciens se sont appuyés sur des équations complexes pour décrire les lois physiques de tout, des tourbillons d'ouragan à la portance des ailes d'avion. Cependant, la formation de singularités ou d'explosions dans les fluides reste l'un des problèmes mathématiques les plus fondamentaux et non résolus. Ce phénomène désigne :Lorsque la résolution des équations gouvernantes (telles que les équations d'Euler tridimensionnelles) part de conditions initiales lisses, des gradients infinis peuvent évoluer.

Les méthodes numériques traditionnelles identifient principalement les singularités stables, qui sont des résultats robustes pouvant être obtenus même avec de légères perturbations des conditions initiales. En revanche, les singularités instables sont extrêmement difficiles à capturer, car elles nécessitent un ajustement infiniment précis des conditions initiales.Car dans cet état hautement instable, même une petite perturbation entraînera immédiatement une déviation de la solution de la trajectoire d’explosion.Cependant, pour certains problèmes clés non résolus, tels que les cas d’Euler et de Navier-Stokes sans frontières, de nombreuses spéculations existent dans la communauté mathématique selon lesquelles les singularités instables pourraient jouer un rôle crucial.

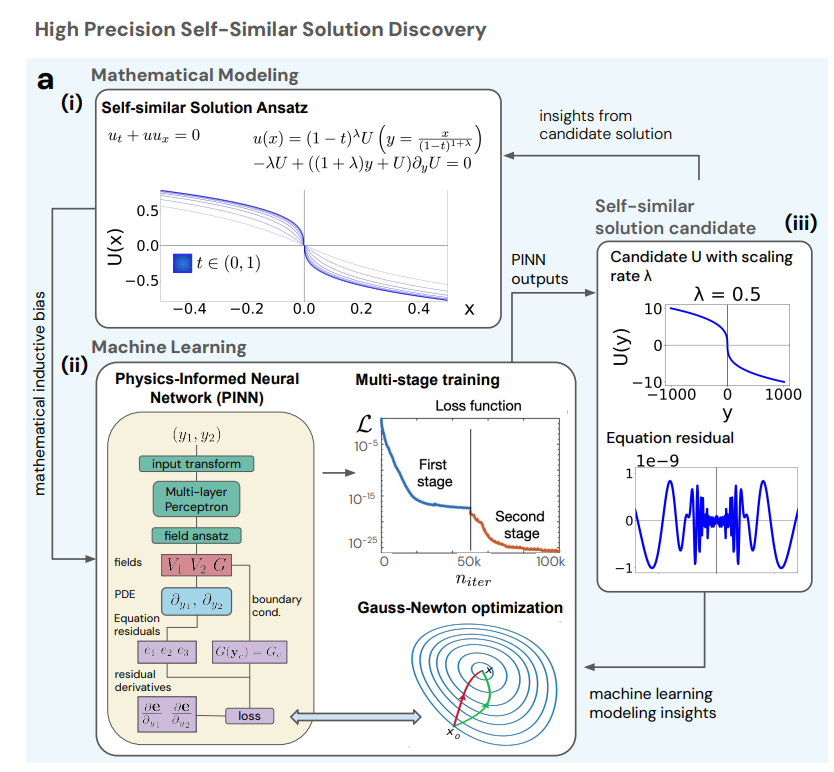
En réponse à ce problème non résolu depuis un siècle,Les chercheurs ont procédé en deux étapes : la découverte de solutions et l’analyse de solutions.Réalisez une découverte de haute précision de singularités instables.

d'abord,Les chercheurs ont utilisé une solution candidate pour rechercher des solutions explosives avec un facteur d'échelle auto-similaire λ et leur distribution spatiale auto-similaire, comme illustré dans la figure (i) ci-dessous, pour l'équation de Burgers. Ils ont ensuite utilisé une approche itérative pour optimiser en continu le processus d'apprentissage automatique et la précision de la solution (illustrée dans la figure ii ci-dessous). Les résultats empiriques et la précision de la solution candidate ont guidé la modélisation mathématique et la conception de l'architecture du réseau neuronal, ce qui a ensuite influencé les biais inductifs dans l'architecture du réseau, tels que la transformation des coordonnées d'entrée et la conception morphologique du champ de sortie.

Dans ce processus, les chercheurs ont utilisé un réseau neuronal d'information physique (PINN), combiné à un optimiseur Gauss-Newton et à une stratégie de formation en plusieurs étapes, pour générer des solutions candidates de haute précision tout en trouvant le facteur d'échelle λ correct.

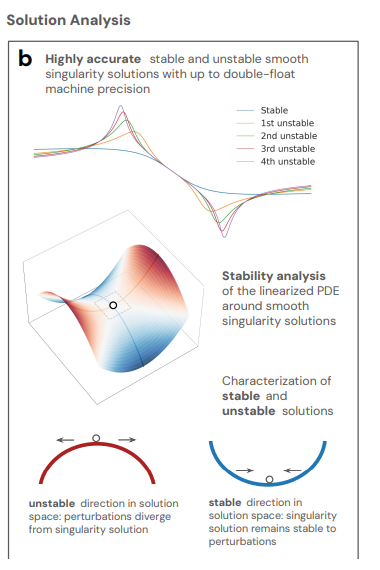
Deuxièmement,Lors de l'analyse des solutions, pour chaque solution instable trouvée pour les équations CCF, IPM et Boussinesq, les chercheurs ont analysé sa stabilité en linéarisant les équations aux dérivées partielles qui l'entouraient. Pour chaque n-ième solution instable trouvée, les chercheurs ont identifié n modes instables partageant les mêmes hypothèses de symétrie que la solution.

Ces modes instables indiquent des directions à suivre pour orienter la solution vers une plus grande stabilité, démontrant que la famille de solutions découverte est complète dans la plage de valeurs admissibles de λ considérée. Cela permet aux chercheurs de caractériser non seulement le degré de stabilité, mais aussi de découvrir des singularités stables et instables avec une grande précision.

Des connaissances mathématiques et des réseaux neuronaux font de PINN une nouvelle arme

Dans cette étude, les réseaux de neurones d'information physique ont acquis une puissance accrue, dépassant leur rôle habituel d'outil général de résolution d'équations aux dérivées partielles. L'équipe de recherche a représenté la solution sous la forme d'une fonction lisse paramétrée par le réseau de neurones.Permet d'intégrer des informations mathématiques directement dans les architectures de réseaux neuronaux, guidant le processus d'optimisation vers des solutions mathématiquement pertinentes.

L'équipe de recherche a utilisé la conception architecturale pour appliquer les contraintes dérivées des équations de référence, telles que la symétrie, la périodicité et la gestion des domaines infinis, fournissant ainsi un paramètre d'apprentissage standard robuste. En optimisant itérativement l'architecture du réseau grâce à une boucle de rétroaction d'expériences numériques et d'analyses mathématiques, ils ont explicitement pris en compte ce comportement et réécrit les équations restantes, améliorant ainsi significativement la stabilité de l'optimisation.

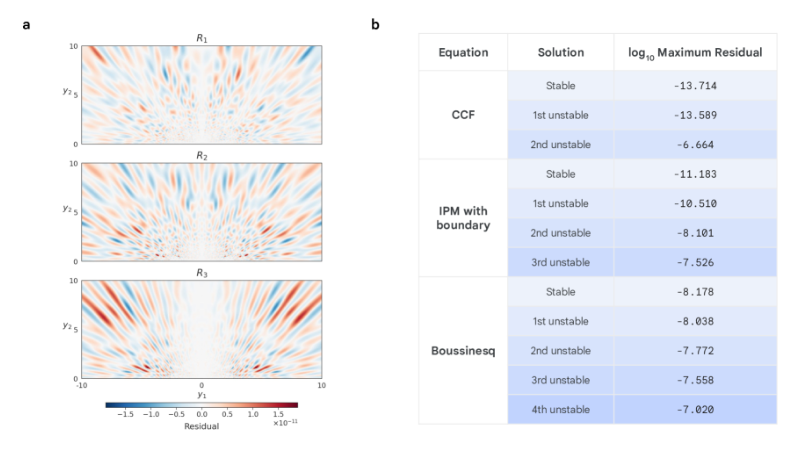
Formation de haute précision améliorée

Afin de répondre à la précision extrêmement élevée requise pour les singularités instables, les chercheurs ont apporté deux améliorations clés au processus de formation.L'optimiseur Gauss-Newton et la formation en plusieurs étapes sont introduits pour une formation de haute précision.

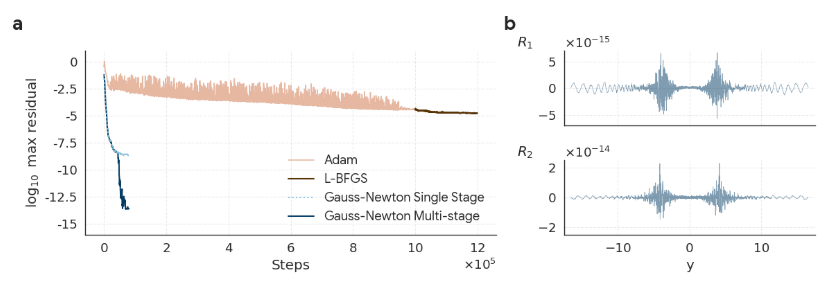
L'adoption de cet optimiseur s'explique par le fait que les optimiseurs de gradient standards actuels (tels qu'Adam ou L-BFGS) ne permettent pas de produire des solutions de haute qualité à l'équation. Par conséquent, l'équipe de recherche a opté pour la méthode d'optimisation de Gauss-Newton, plus puissante, pour optimiser le réseau neuronal. Compte tenu de la petite taille du réseau, cette solution, jusqu'alors irréalisable, a été couronnée de succès. Les résultats expérimentaux montrent que la méthode de Gauss-Newton permet de réduire l'erreur résiduelle à 10⁻⁸ en environ 50 000 itérations.Il présente de meilleures performances et une convergence nettement plus rapide que l'optimiseur de gradient standard.

en bref,L'idée de la formation en plusieurs étapes est de former d'abord un réseau pour obtenir une solution approximative, puis de former un deuxième réseau pour corriger spécifiquement les erreurs que le réseau précédent n'a pas bien gérées.La combinaison des résultats des deux réseaux permet d'améliorer la précision de la solution. Lors d'expériences sur des solutions stables et instables du premier ordre des équations CCF et IPM, la méthode d'apprentissage en plusieurs étapes a permis d'améliorer le résidu maximal de cinq ordres de grandeur, une précision suffisante pour satisfaire à la vérification mathématique rigoureuse basée sur la méthode CAP.

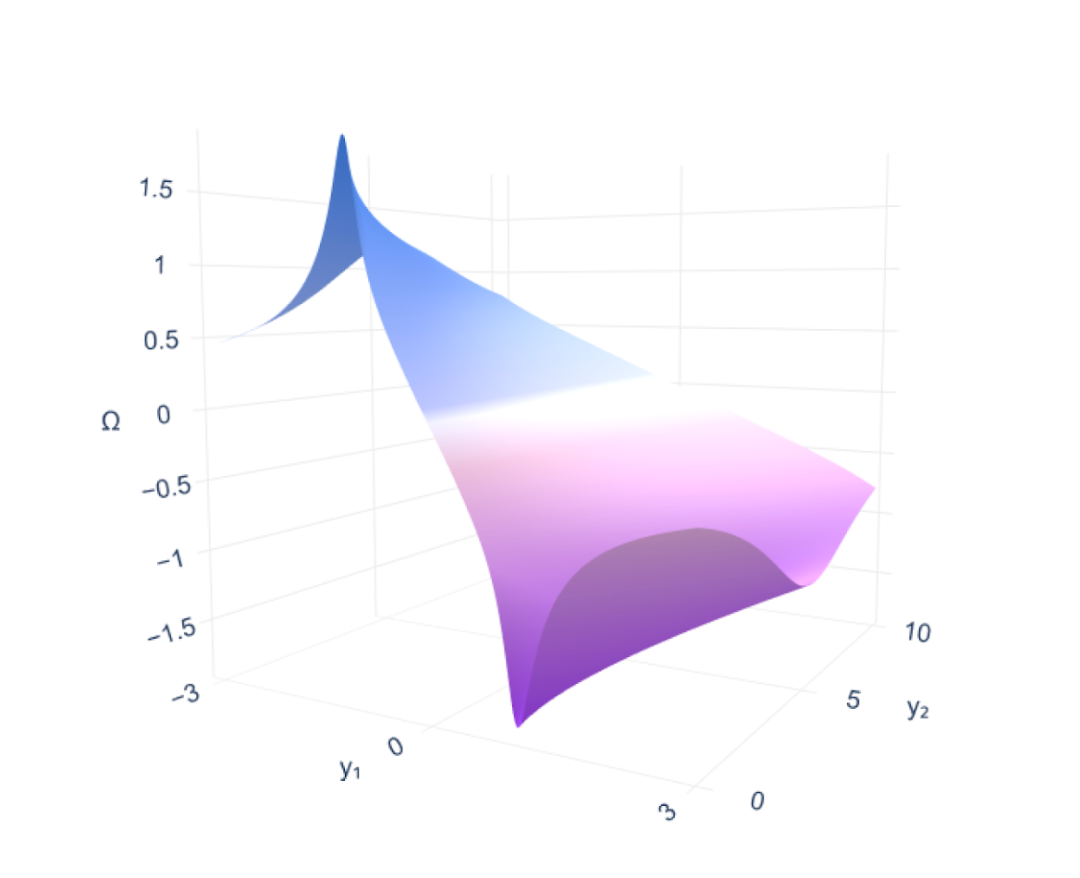
Cette approche permet au modèle d'atteindre un niveau de précision inédit. En utilisant la visualisation tridimensionnelle et l'analyse de champs de vorticité bidimensionnels comme exemples de référence, l'équipe de recherche a démontré une mesure du degré de rotation du fluide en chaque point. L'erreur maximale résolue équivaut à améliorer la précision de la prédiction du diamètre terrestre à quelques centimètres près.

Document 1 En tant que doctorant chinois

Yongji Wang, auteur principal de l'article, est actuellement chercheur postdoctoral au Courant Institute of Mathematical Sciences de l'Université de New York et chercheur postdoctoral invité à l'Université de Stanford. Ses recherches portent sur la mécanique des milieux continus, la géophysique et l'apprentissage automatique scientifique. Il possède une vaste expérience de l'application de techniques théoriques et numériques pour élucider des processus physiques complexes dans la nature et l'environnement.

La recherche se concentre sur le développement de techniques d’apprentissage profond de haute précision pour un large éventail de problèmes scientifiques, allant de la révélation des propriétés physiques cachées des plates-formes de glace de l’Antarctique à la recherche de solutions explosives auto-similaires aux équations aux dérivées partielles non linéaires (EDP).

Références :
1.https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/
2.https://english.elpais.com/science-tech/2025-06-24/spanish-mathematician-javier-gomez-serrano-and-google-deepmind-team-up-to-solve-the-navier-stokes-million-dollar-problem.html

3.https://mp.weixin.qq.com/s/CRlGLmji4BWNkNaA7e2JEw