Command Palette
Search for a command to run...
En Collectant Plus De 20 Ensembles De Données spatio-temporelles Et Plus De 130 Millions De Points d'échantillonnage, l'équipe De Recherche De Tsinghua a Proposé 3 Méthodes De Modélisation De Systèmes Urbains Complexes Basées Sur l'IA générative.

Michael Batty, connu comme l'un des pionniers de l'étude des systèmes urbains complexes, a déclaré un jour dans son livre :« Les villes sont essentiellement des systèmes adaptatifs complexes dont les structures et les fonctions évoluent constamment et présentent des caractéristiques hautement non linéaires et auto-organisées. »Avec le développement continu des villes modernes, la complexité des systèmes urbains augmente.
Cette complexité rend difficile pour les méthodes de modélisation traditionnelles d’y faire face. Cependant, avec le développement de la technologie de l’IA générative, la modélisation générative, en tant que moyen technique émergent, devient progressivement un outil important pour étudier et comprendre les systèmes urbains. Les modèles génératifs de systèmes urbains complexes peuvent non seulement simuler l’évolution de la structure urbaine, mais également générer des schémas d’urbanisme innovants, fournissant de nouvelles idées pour les villes intelligentes et le développement durable.
En se concentrant sur la situation nationale, la recherche sur les modèles génératifs de systèmes urbains complexes a fait des progrès significatifs ces dernières années, et de nombreuses universités et instituts de recherche ont obtenu des résultats fructueux.
Récemment, lors du forum COSCon'24 AI for Science produit conjointement par HyperAI,Ding Jingtao, chercheur postdoctoral du Centre de recherche en sciences urbaines et informatiques du Département de génie électronique de l'Université Tsinghua, a prononcé un discours intitulé « Modélisation pilotée par l'IA et découverte de lois des systèmes urbains complexes ».Nous avons donné une explication approfondie de la méthode de modélisation générative spatio-temporelle pour les systèmes urbains complexes et des derniers progrès de recherche de l’équipe.
HyperAI a compilé et résumé le partage approfondi du Dr Ding Jingtao sans violer l'intention initiale. Voici la transcription du discours.
Concentrez-vous sur la modélisation générative des systèmes urbains complexes et découvrez les modèles de distribution des données
Les recherches de notre équipe dans le domaine des villes intelligentes et de l'informatique urbaine portent sur la modélisation de systèmes urbains complexes.En tant que système complexe, la ville est similaire au fonctionnement de la nature dans un écosystème. Les humains qui y vivent interagissent avec le système urbain dans de multiples dimensions, formant des interactions complexes. Par exemple, au cours du processus de construction urbaine, divers systèmes de réseaux ont été formés, notamment un réseau de transport, un réseau de communication et un réseau d’alimentation électrique. L’imbrication des éléments du réseau au niveau physique et des éléments sociaux de la vie humaine exacerbe encore la complexité des systèmes urbains.

En réponse à cela, les recherches de notre équipe se concentrent principalement sur les trois types de problématiques suivantes :
(1) Le problème de la prédiction de l’évolution des états urbains,Autrement dit, nous devrions nous concentrer sur la direction et le processus du développement futur de la ville, car le développement urbain est essentiellement un processus dynamique de changement spatio-temporel, ce qui constitue un problème typique de prédiction spatio-temporelle ;
(2) Simulation et déduction d'éléments urbains,Similaire au concept de jumeaux numériques ou de métavers, un environnement numérique est construit à partir de données réelles et déduit sur la base de celles-ci pour résoudre les problèmes « et si » dans des scénarios hypothétiques ;
(3) Problème d'optimisation de la prise de décision en matière de gouvernance urbaine,Sur la base des prévisions et simulations d’évolution urbaine mentionnées ci-dessus, les décisions de gouvernance urbaine peuvent être optimisées pour résoudre des problèmes urbains spécifiques tels que les embouteillages et les catastrophes naturelles.
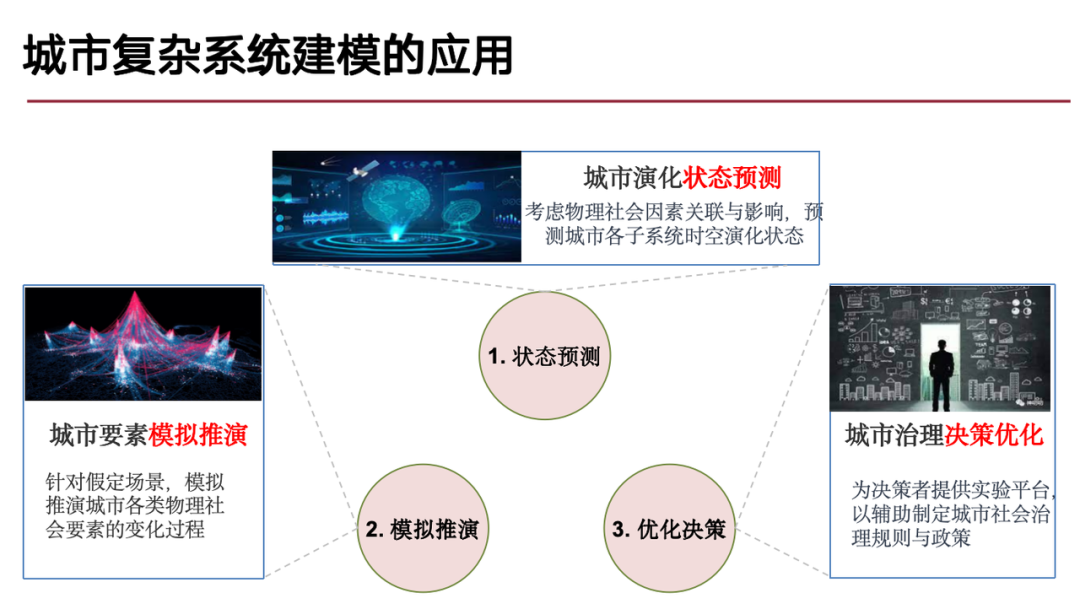
Les recherches actuelles de notre équipe portent sur la modélisation générative de systèmes urbains complexes.Le cœur du modèle génératif est d’apprendre la distribution de probabilité derrière les données, c’est-à-dire de modéliser la distribution de probabilité en fonction des données observées et de capturer le processus de génération des données.Si le modèle possède cette capacité, il peut résoudre efficacement les trois types de problèmes ci-dessus.
Présentation des méthodes d'IA générative pour résoudre les défis de modélisation
L'IA générative se développe actuellement rapidement, principalement sous deux aspects : l'un est le développement de la technologie de génération de langage représentée par de grands modèles de langage, et l'autre est le progrès de la technologie de génération de contenu visuel représentée par des modèles de diffusion.La question de savoir si la méthode d’IA générative est applicable à la modélisation de systèmes urbains complexes devient la clé de nos recherches.
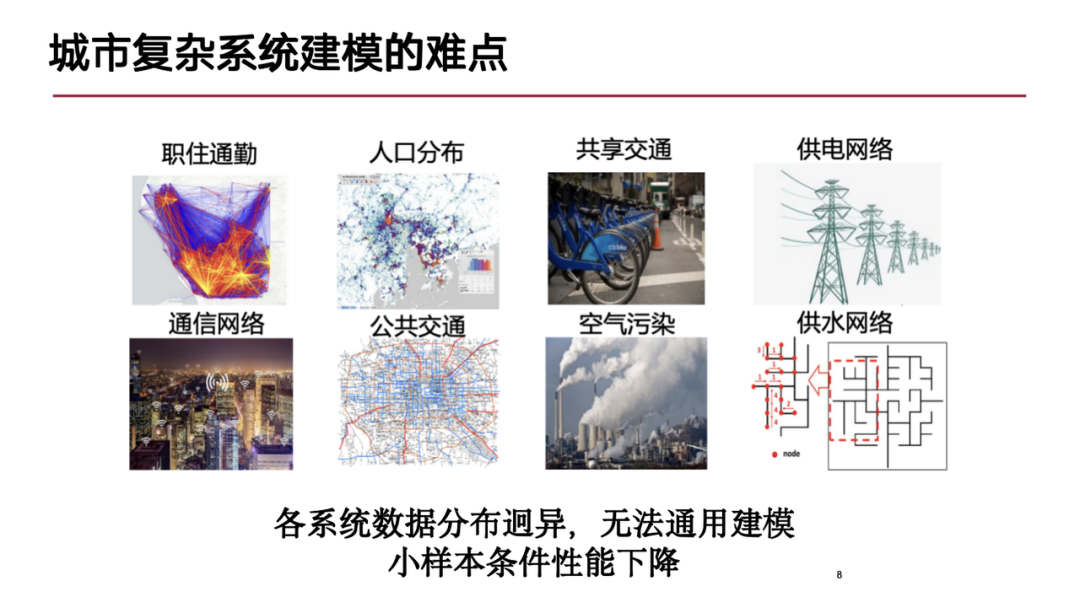
Dans les systèmes urbains complexes, les difficultés de modélisation se reflètent principalement dans les aspects suivants :nouille:Premièrement, les systèmes urbains complexes présentent des caractéristiques spatio-temporelles importantes et les modalités de données sont très riches, incluant de multiples formes de données spatio-temporelles, telles que les données de trajectoire des déplacements des piétons dans la ville, qui sont similaires aux données de séquence du langage naturel ; en outre, il existe des données de grille spatiotemporelles utilisées pour prévenir les accidents de bousculade et les structures topologiques de la ville (comme la structure graphique formée par les routes et les bobines de mesure de vitesse). Le mélange de ces différentes données spatio-temporelles modales pose des défis de modélisation.

Deuxièmement, du point de vue des systèmes urbains complexes, une ville est un système géant composé de multiples sous-systèmes. Ces sous-systèmes présentent des interactions complexes en leur sein, et il existe un certain degré de couplage entre différents sous-systèmes (tels que les systèmes électriques et les systèmes de réseaux de communication). L’interdépendance et les interactions complexes de ces sous-systèmes imposent des exigences plus élevées en matière de modélisation.

Enfin, le système urbain est un processus dynamique. Différents sous-systèmes peuvent collecter une variété de données, et ces données ont des formes, des modes et des distributions différents, ce qui rend difficile leur modélisation universelle. Il s’agit également d’un problème difficile à surmonter au stade actuel de la recherche.
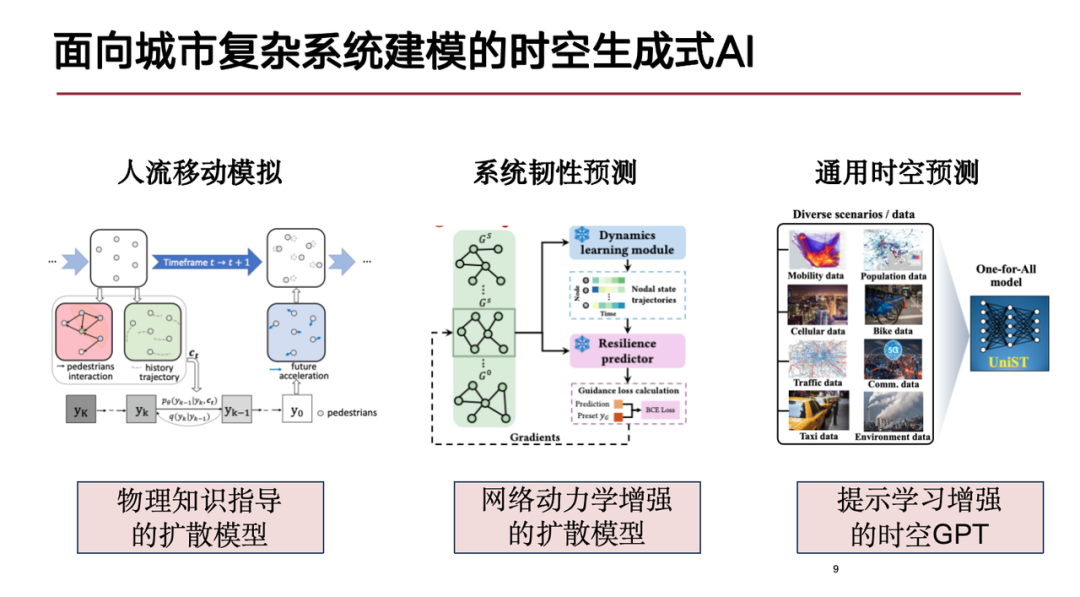
Sur la base des défis ci-dessus, je présenterai aujourd’hui nos progrès de recherche dans les trois domaines suivants :La première est la simulation du flux de personnes.Nous proposons un modèle de diffusion guidé par les connaissances physiques pour déduire plus précisément le mouvement des personnes dans les villes ;Le deuxième est la prédiction de la résilience des systèmes complexes ; et le dernier est le modèle général de prédiction de l'espace-temps.
Simulation des mouvements de foule — Modèle de diffusion guidé par les connaissances physiques
L’objectif de la simulation de flux piétonnier est de reproduire le mouvement dynamique et le processus d’interaction d’un grand nombre de piétons dans l’espace. Le problème central est le suivant : étant donné les points de départ et d’arrivée des piétons ou des individus, générer leurs trajectoires au cours du processus de déplacement.Cette simulation est d’une grande valeur dans de nombreux scénarios d’application, tels que la planification de chemin pour les personnages virtuels (PNJ) dans les jeux et l’analyse de faisabilité des conceptions de bâtiments dans la vie réelle. Afin de tester les performances des conceptions architecturales dans des scénarios spécifiques, il est généralement nécessaire de simuler des flux piétonniers à grande échelle.

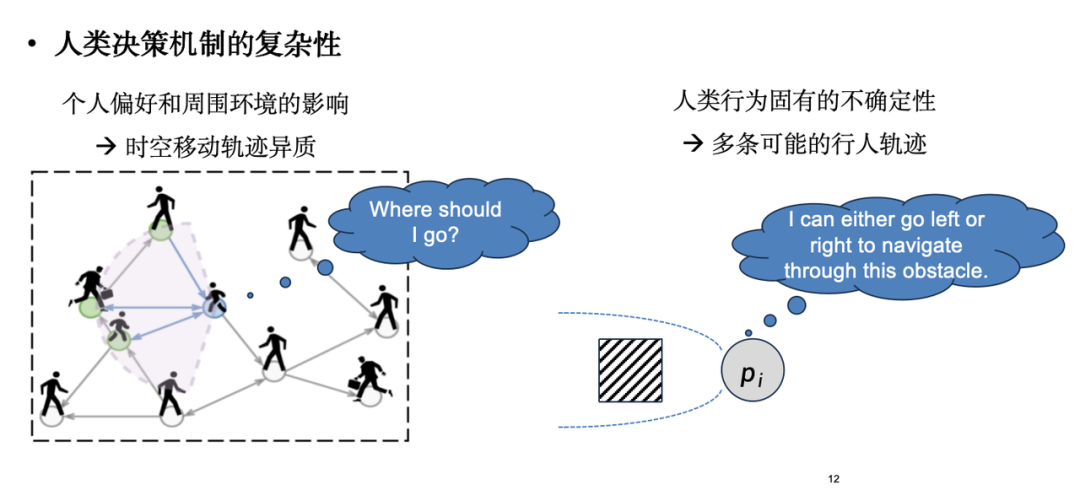
Cependant, le principal défi de la simulation des flux humains est que l’objet de la simulation n’est pas un système moléculaire avec des lois physiques claires, mais un individu doté de capacités de prise de décision autonomes : les humains.Les mécanismes de prise de décision des individus sont complexes et changeants : d’une part, les préférences individuelles sont affectées par l’environnement qui les entoure, ce qui entraîne un ajustement constant de leurs décisions ; D’un autre côté, le comportement humain comporte une incertitude inhérente. Par exemple, face à un obstacle, différents individus choisiront différentes stratégies d’adaptation (certains choisissent d’aller à gauche, d’autres choisissent d’aller à droite), et cette incertitude est difficile à décrire avec une formule déterministe.
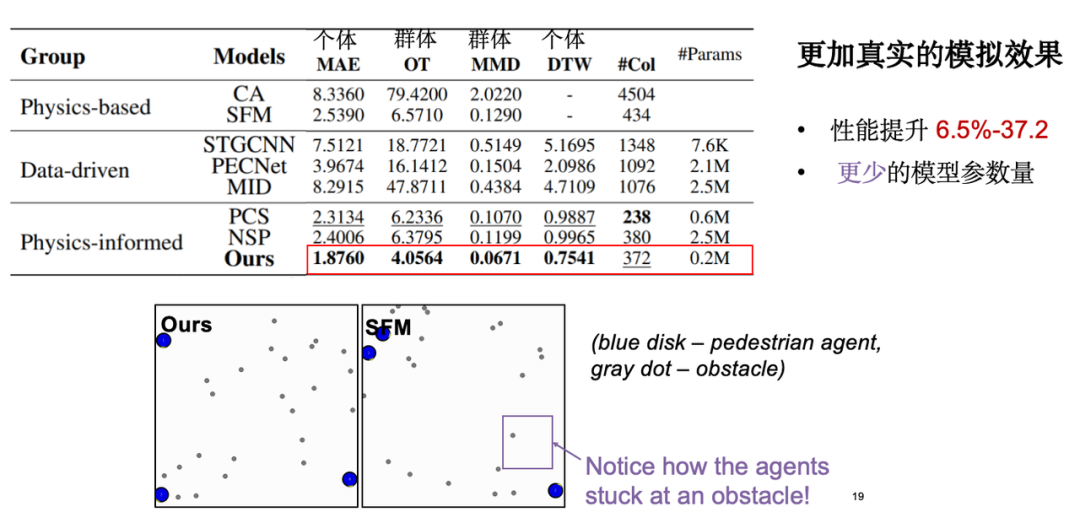
Dans les applications pratiques, le modèle de simulation de flux de foule le plus largement utilisé est le « modèle de force sociale », qui provient des idées de la mécanique newtonienne et est l'une des méthodes classiques basées sur l'ABM (Agent-Based Modeling).Le modèle de force sociale considère le mouvement humain comme un processus déterminé par la force. Comme le montre la figure ci-dessous, lorsque les individus se déplacent, ils sont non seulement attirés par la destination, mais également repoussés par les obstacles et les piétons environnants. Cependant, un examen plus approfondi révèle que le modèle de force sociale ne parvient pas à saisir les caractéristiques subtiles des données réelles.

Nous explorons donc comment combiner les techniques d’IA générative,Intégrer les connaissances en physique dans les modèles de diffusion.La raison du choix du modèle de diffusion est que le mécanisme de prise de décision humaine est intrinsèquement incertain et constitue un processus de génération de probabilités. Le modèle de diffusion fonctionne bien dans la modélisation de la distribution de données à haute dimension et convient à la simulation de tels problèmes d’incertitude.
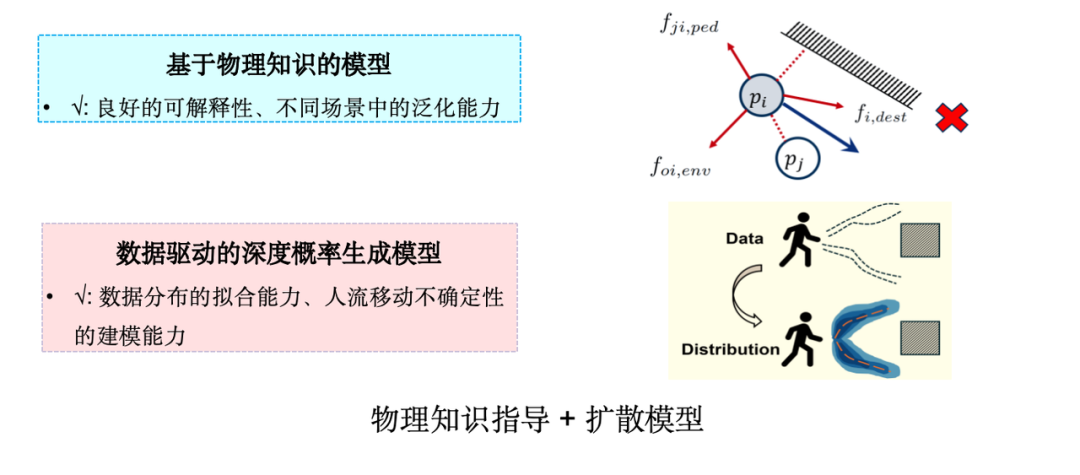
Nous avons conçu un réseau neuronal graphique basé sur le modèle de force sociale, incorporé les termes d'attraction et de répulsion de la force sociale dans le modèle et proposé un modèle de simulation de flux de foule SPDiff.
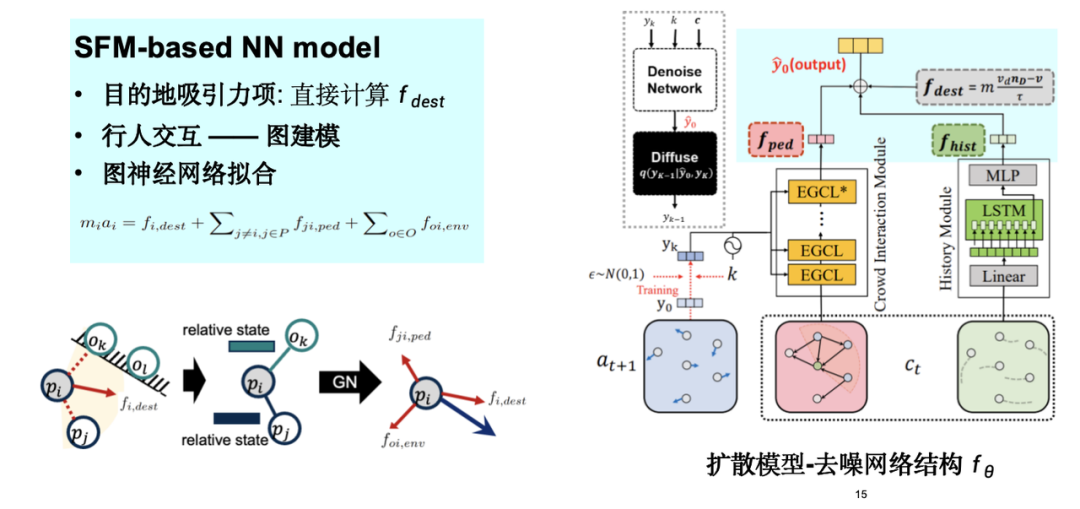
Comme le montre la figure ci-dessous, nous avons pris en compte les symétries cachées dans les données de mouvement de foule, telles que la rotation et la translation, et les avons incorporées dans le processus de conception du modèle. L’injection de ce biais inductif permet d’optimiser l’ensemble du processus de simulation.
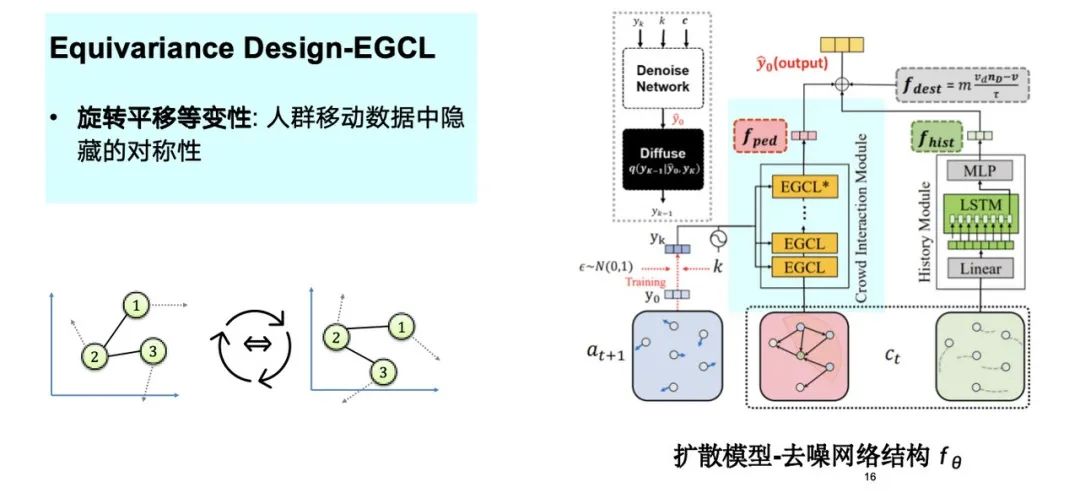
Nous avons sélectionné un ensemble de données de mouvements piétonniers réels pour évaluer les performances du modèle. Les sources de données comprennent les données de surveillance sur les places des gares et les mouvements des piétons dans les rues.
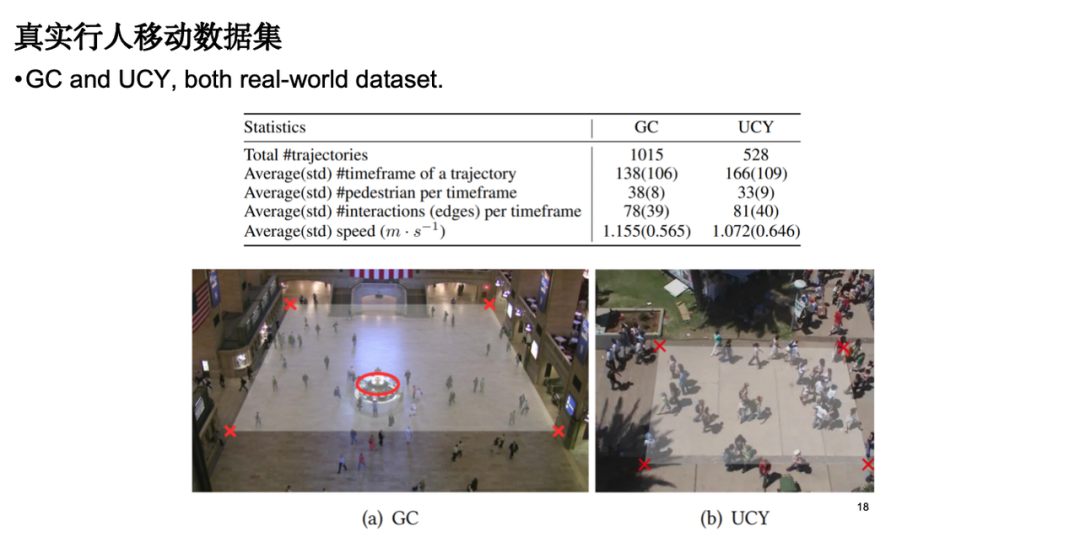
Les indicateurs suivants sont principalement concernés par l’évaluation du modèle :La première est l’erreur de mouvement individuel, c’est-à-dire l’erreur absolue entre la trajectoire simulée et la trajectoire réelle observée ; le deuxième est l'indice de distribution de groupe, c'est-à-dire que nous espérons que la trajectoire simulée est proche des données réelles au niveau de la distribution. De plus, nous avons également effectué une analyse de visualisation et les résultats ont montré que, par rapport au modèle classique de force sociale, notre modèle fonctionnait de manière plus raisonnable en termes d’effet d’évitement des obstacles. Il convient de mentionner qu’après l’introduction des connaissances physiques, le nombre de paramètres du modèle a été considérablement réduit, optimisant ainsi l’efficacité du modèle.
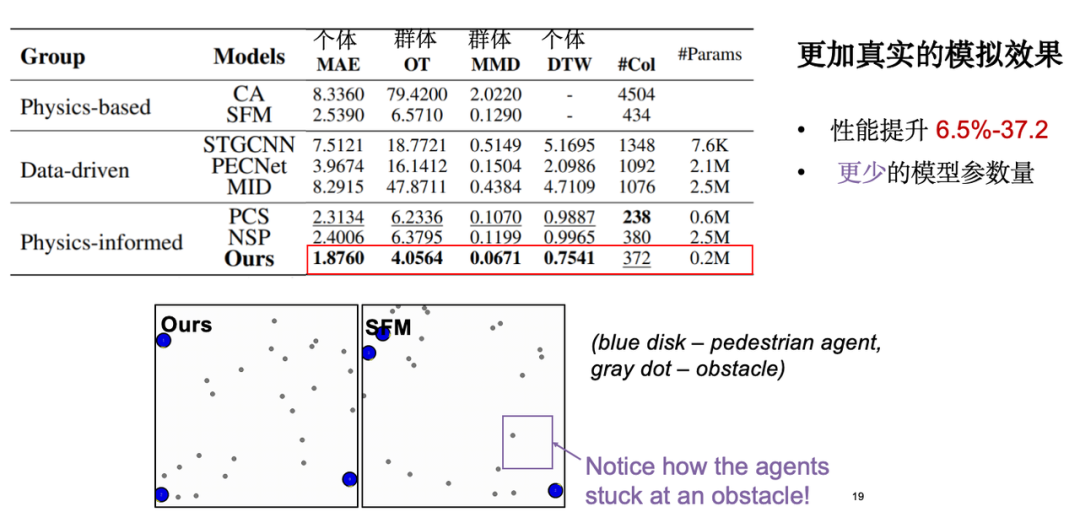
En explorant plus en détail l’introduction des connaissances physiques, nous avons constaté que l’équivariance confère au modèle un avantage dans l’apprentissage sur petits échantillons. Comme mentionné précédemment, la trajectoire de déplacement est essentiellement symétrique après rotation et translation.Par conséquent, le modèle n’a besoin que d’un petit nombre d’échantillons de données pour réaliser un apprentissage efficace.Les expériences montrent que lorsque la quantité de données d’entraînement est réduite à 5%, l’effet du modèle est toujours proche des performances de l’ensemble de données complet.
La recherche connexe était intitulée « Modèle de diffusion informé par la physique sociale pour la simulation de foule » et « Comprendre et modéliser le comportement d'évitement des collisions pour une simulation de foule réaliste », publiées respectivement dans AAAI 2024 et CIKM 2023, et le code et les données étaient open source.
Adresse du document :https://arxiv.org/abs/2402.06680
Adresse du projet open source :https://github.com/tsinghua-fib-lab/SPDiff
Adresse du document :https://dl.acm.org/doi/10.1145/3583780.3615098
Adresse du projet open source :https://github.com/tsinghua-fib-lab/TECRL
Prédire la résilience du système : un modèle de diffusion amélioré par la dynamique du réseau
La résilience fait référence à la capacité d’un système à maintenir ses fonctions de base lorsqu’il est soumis à des défaillances internes ou à des perturbations externes.Par exemple, pour les écosystèmes, la résilience fait référence à la capacité à maintenir la biodiversité malgré les changements environnementaux. Dans les systèmes sociaux humains, nous espérons que de nombreux systèmes d’ingénierie, tels que les réseaux de chaîne d’approvisionnement, ont une résilience telle qu’ils garantissent la relation normale de production et de vente entre les producteurs et les consommateurs dans des circonstances particulières, maintenant ainsi le fonctionnement normal de l’économie.

D’un point de vue théorique, il existe quelques définitions classiques de la résilience du réseau. La résilience peut être considérée comme un état de nœud, représenté par x, qui reflète si le système peut converger vers le seul état stable attendu après qu'une perturbation a été appliquée à un nœud.Si un système est résilient, il peut revenir à son état attendu dans un certain laps de temps même s’il est perturbé ; s’il manque de résilience, il sera difficile de s’en remettre. Comme le montre la figure ci-dessous, les systèmes résilients peuvent revenir à un état stable après une perturbation, tandis que les systèmes non résilients peuvent ne pas être en mesure de récupérer.
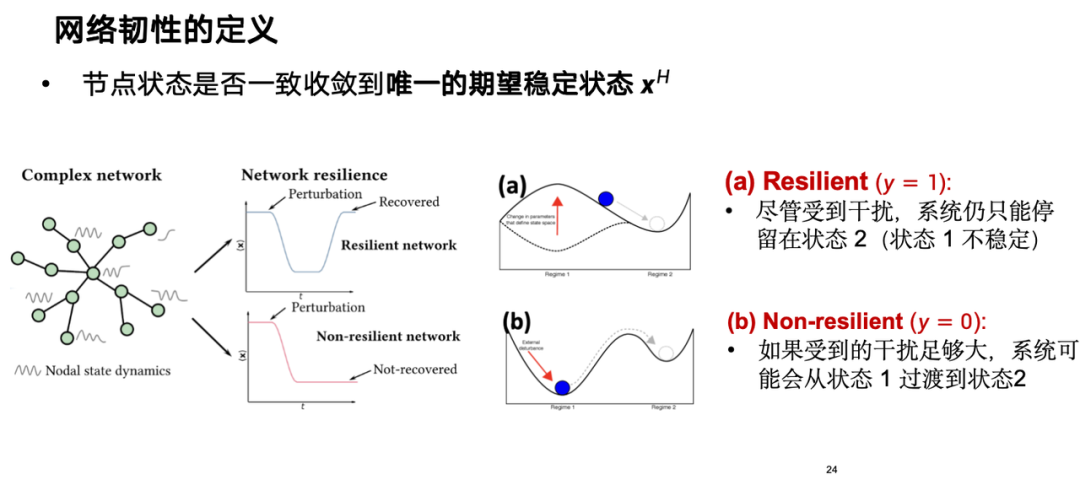
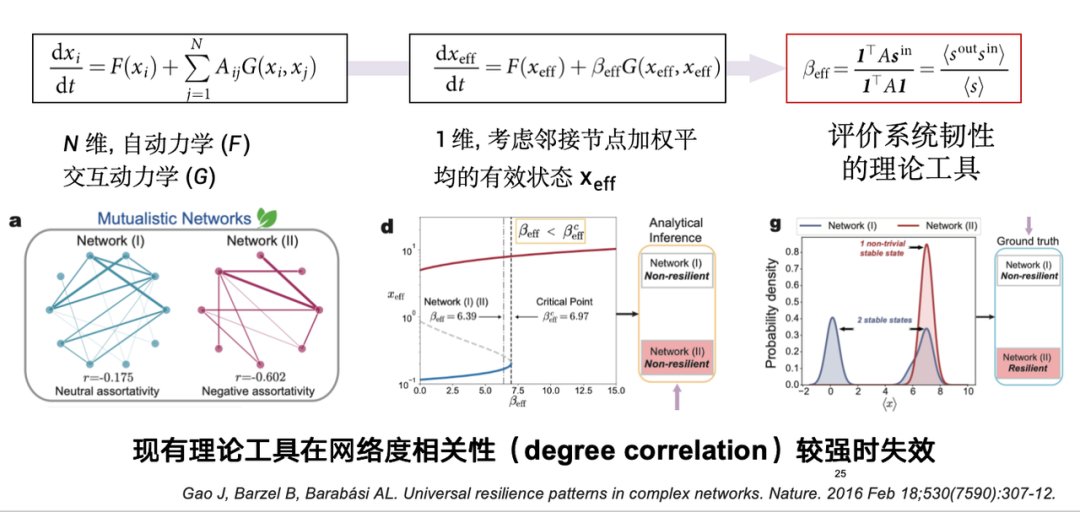
Dès 2017, un article de Nature proposait une méthode de modélisation théorique, qui est essentiellement l’étude d’un système n-dimensionnel à haute dimension. Le nombre de nœuds dans de tels systèmes peut atteindre des dizaines de milliers, voire des millions.En théorie, cette méthode simplifie un système de grande dimension en une seule dimension par réduction de dimensionnalité afin d'obtenir une expression de la résilience du système.
Cependant, cet outil théorique présente des limites dans les systèmes réels et n’est applicable qu’aux systèmes avec des degrés faiblement corrélés. Cependant, l'effet assortatif-hétéroassocié existe souvent dans les systèmes réels, c'est-à-dire que les valeurs de degré de deux nœuds reliés par une arête peuvent être fortement corrélées. Par conséquent, cet outil présente encore quelques difficultés pour évaluer la résilience des systèmes réels.
Adresse du document :https://www.nature.com/articles/nature16948
Sur cette base, notre équipe a proposé une méthode de modélisation de la résilience du système de réseau basée sur les données.Comme mentionné précédemment, la résilience est affectée par les effets combinés de l’évolution de l’état des nœuds et de la topologie du réseau. Grâce à la modélisation basée sur les données ou sur l’apprentissage automatique, nous divisons le problème en deux dimensions. D’une part, le processus de changement dynamique de l’état du nœud est caractérisé par la trajectoire d’évolution de l’état ; d'autre part, l'influence de la topologie du réseau doit également être prise en compte. Les deux travaillent ensemble pour créer la résilience des systèmes complexes. Sur cette base, nous concevons un modèle de prédiction de résilience basé sur les données.
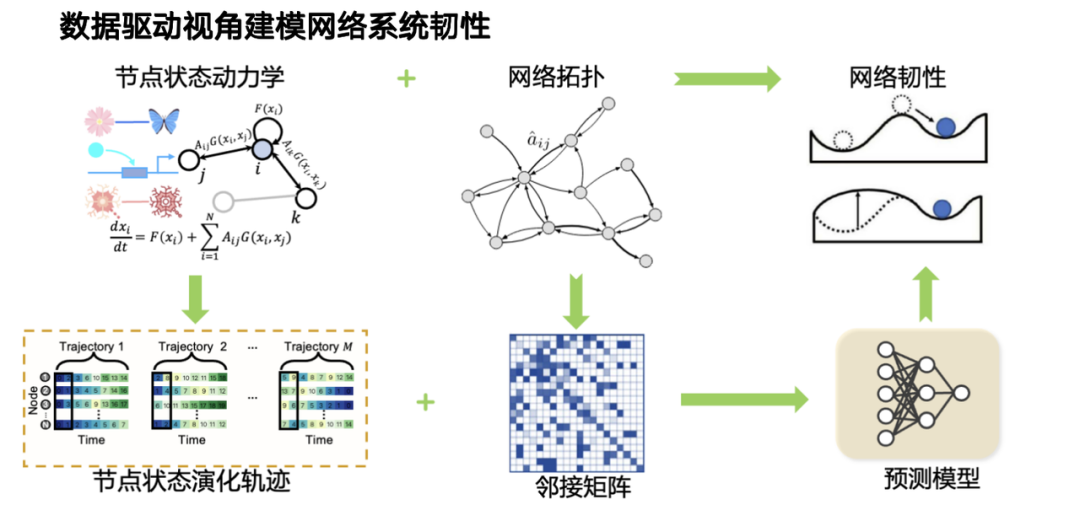
En termes d'architecture de modèle, nous avons conçu une structure qui combine des réseaux de neurones graphiques et Transformer :Pour la partie évolution dynamique, nous utilisons Transformer pour modéliser les relations temporelles ; pour les relations topologiques complexes, nous introduisons des réseaux de neurones graphiques pour modéliser les interactions d'ordre élevé entre les systèmes. Les deux fonctionnent ensemble pour former notre observation de la résilience du système.
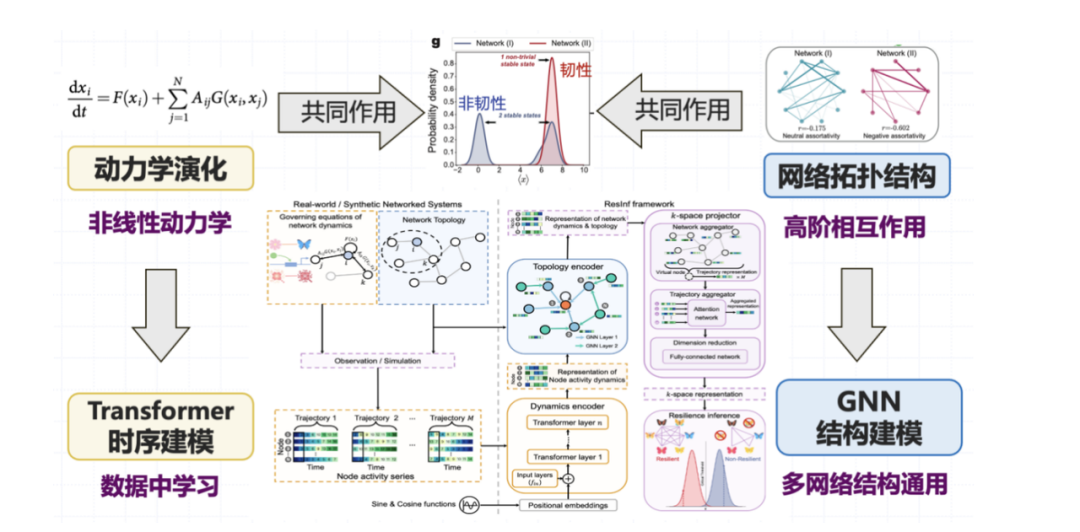
Dans l'expérience, nous avons considéré différents types de dynamiques d'état de nœud, telles que la chaîne d'approvisionnement de l'écosystème, la dynamique de régulation des gènes en biochimie, la dynamique de transmission du signal neuronal en neurosciences, etc. en termes de topologie, nous avons choisi le type de topologie de réseau classique.
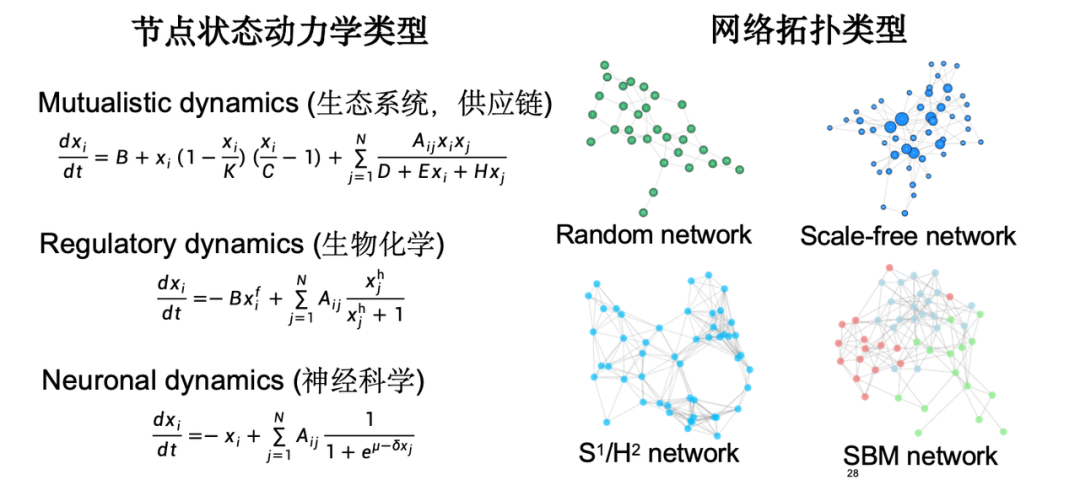
Les résultats expérimentaux montrent que notre modèle a considérablement amélioré la précision de prédiction, un score F1 élevé et un certain degré d'interprétabilité, et réalise une visualisation de réduction de dimensionnalité du plan de décision.
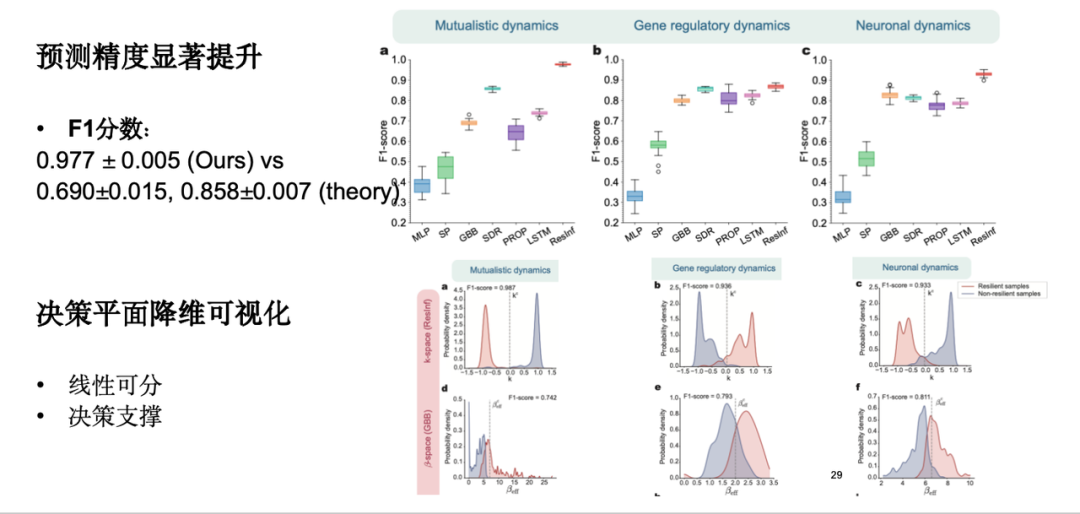
Cependant, dans les applications pratiques, nous constatons que la résilience de la plupart des systèmes est inconnue et qu’il est difficile de déterminer s’ils sont résilients, ce qui entraîne des données d’étiquetage de résilience insuffisantes et des écarts dans les prédictions du modèle. À cette fin, nous améliorons le modèle au niveau de l’échantillon pour le rendre plus robuste dans les cas de petits échantillons.
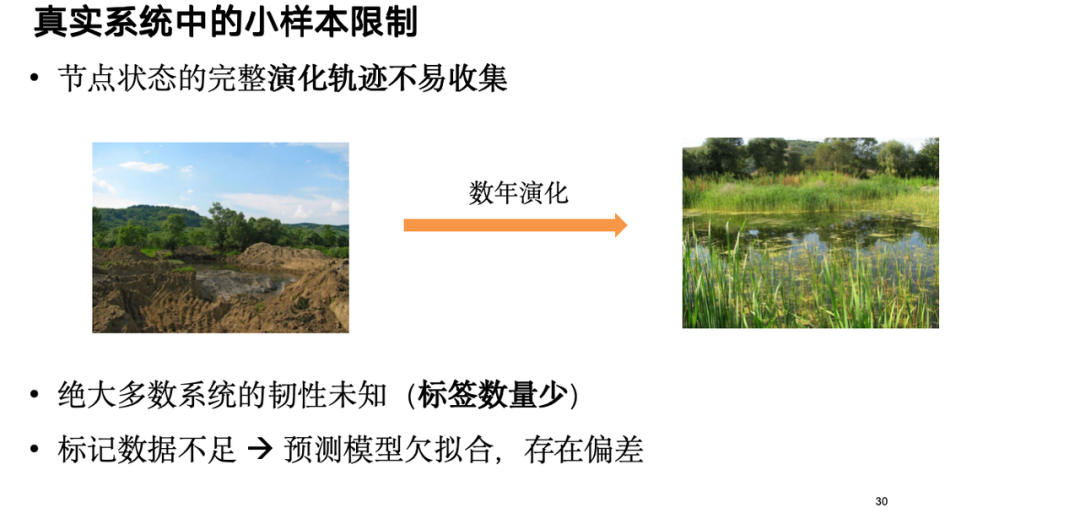
La stratégie spécifique consiste à générer des échantillons d’observation de systèmes résilients et non résilients basés sur le modèle de diffusion pour améliorer le modèle de prédiction. Ces échantillons couvrent la topologie des nœuds et la trajectoire d’évolution de leur état. Dans un premier temps, une amélioration des données est effectuée. Les échantillons améliorés peuvent mieux former le module de prédiction de résilience. Les résultats de la prédiction guident en sens inverse le module d’amélioration des données pour générer des échantillons plus précieux, formant ainsi une boucle de rétroaction positive.
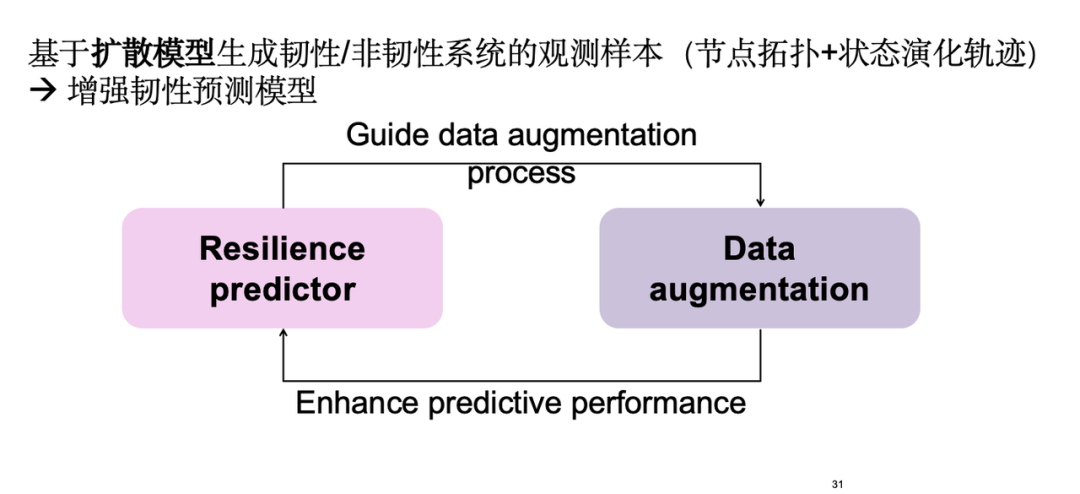
En exploitant la puissance génératrice contrôlable du modèle de diffusion, à savoir la technique de guidage du classificateur, nous générons des échantillons avec le niveau de résilience souhaité, obtenant ainsi une augmentation des données.
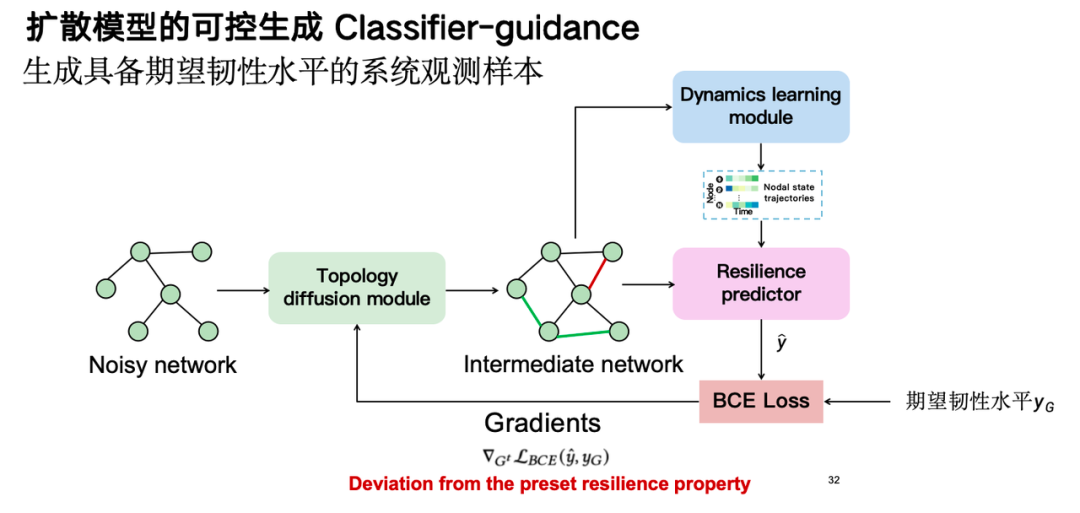
Les résultats des tests sur petits échantillons montrent qu'après l'amélioration du modèle de diffusion, la précision de prédiction du modèle peut atteindre 87% en utilisant seulement 20 échantillons ;Sans amélioration des données, la précision de prédiction du modèle n'est que de 62%. Il convient de mentionner que nous pouvons obtenir une précision de prédiction similaire avec une durée d’observation plus courte de la trajectoire d’évolution de l’état, ce qui est d’une grande importance pour les systèmes qui ne peuvent pas être observés pendant une longue période dans les observations réelles.

La recherche connexe s'intitulait « Deep learning resilience inference for complex networked systems » et « TDNetGen : Empowering Complex Network Resilience Prediction with Generative Augmentation of Topology and Dynamics », publiée respectivement dans Nature Communications et KDD 2024, et le code et les données étaient open source.
Adresse du document :
https://www.nature.com/articles/s41467-024-53303-4
Adresse du projet open source :
https://github.com/tsinghua-fib-lab/ResInf
Adresse du document :
https://arxiv.org/abs/2408.09825
Adresse du projet open source :
https://github.com/tsinghua-fib-lab/TDNetGen
Prédiction spatiotemporelle générale - Apprentissage rapide GPT spatiotemporel amélioré
Depuis 2017, les problèmes de prédiction spatiotemporelle attirent progressivement l’attention dans le domaine de l’apprentissage profond. Les méthodes de recherche actuelles sont principalement divisées en deux catégories : l’une consiste à concevoir des modèles d’apprentissage profond correspondants basés sur les caractéristiques spatio-temporelles de types ou de sources de données spécifiques ; l'autre consiste à modéliser du point de vue des systèmes complexes ou des mathématiques appliquées, en utilisant des méthodes de systèmes dynamiques telles que les calculs de réservoir. Le point commun entre ces deux méthodes est qu’elles modélisent toutes deux un seul sous-système.
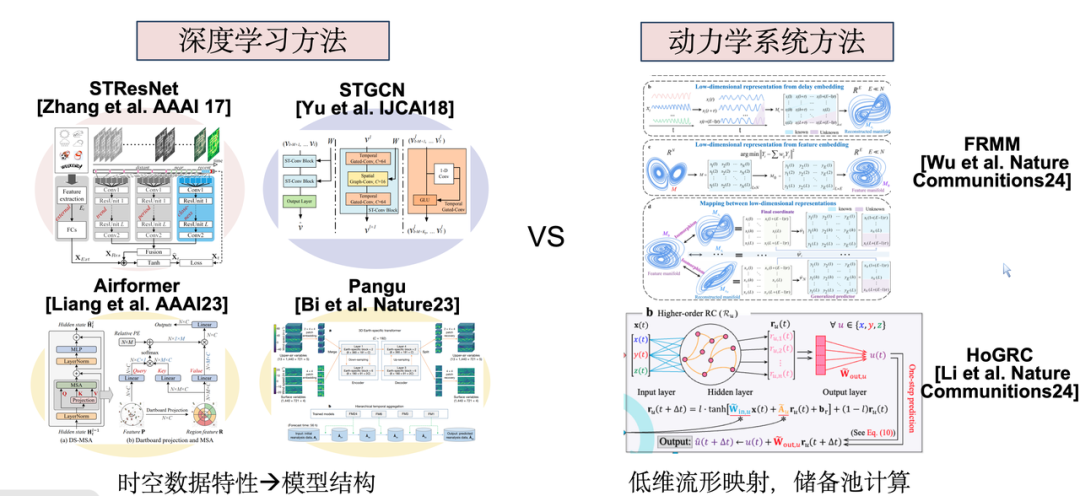
Cependant, pour les systèmes urbains, en raison de la forte corrélation entre les sous-systèmes réels, nous espérons parvenir à une modélisation conjointe afin d'obtenir un effet synergique de 1 + 1 > 2. C'est également l'objectif principal de nos travaux de recherche.
Dans ce cadre, notre conception repose sur la faisabilité suivante : bien que différents types de données spatio-temporelles diffèrent dans leur forme organisationnelle et leur distribution, elles proviennent toutes essentiellement de la production humaine et de la vie dans les villes et sont l'incarnation d'un mécanisme universel sous-jacent dans différentes dimensions. Par conséquent, tant que la méthode appropriée peut être trouvée, ces données hétérogènes peuvent être intégrées pour obtenir un effet synergique de 1 + 1 > 2.
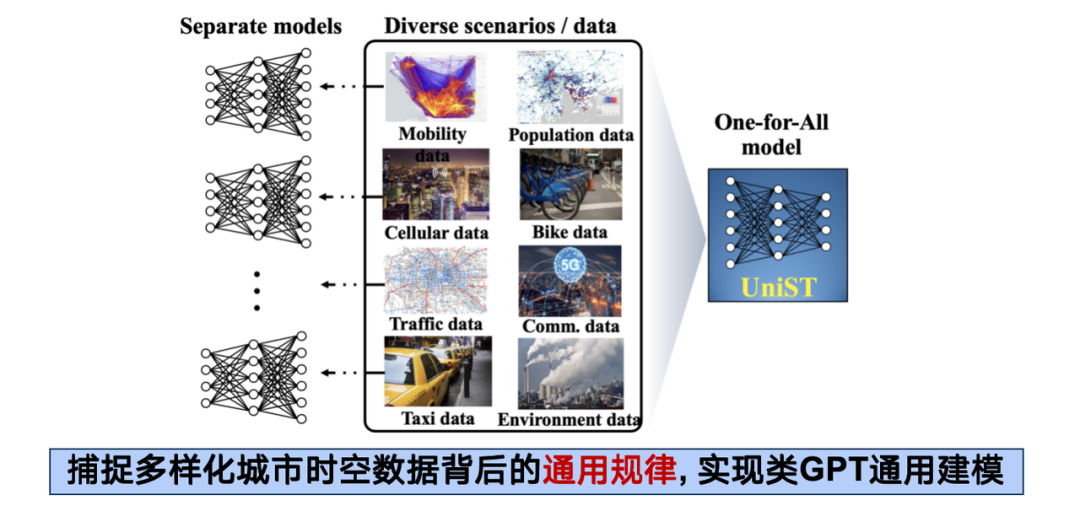
En pratique, nous avons collecté plus de 20 ensembles de données spatio-temporelles et plus de 130 millions de points d’échantillonnage, couvrant cinq sous-systèmes tels que les transports, les réseaux cellulaires et la pollution de l’air, et couvrant 14 villes au pays et à l’étranger.
En termes de conception de modèles, nous avons poursuivi l'architecture Transformer, modélisé diverses formes de données spatio-temporelles sous forme de tenseurs de haute dimension et les avons traitées d'une manière similaire à ViT (Vision Transformer).Finalement, le modèle universel de prédiction spatiotemporelle UniST a été formé.
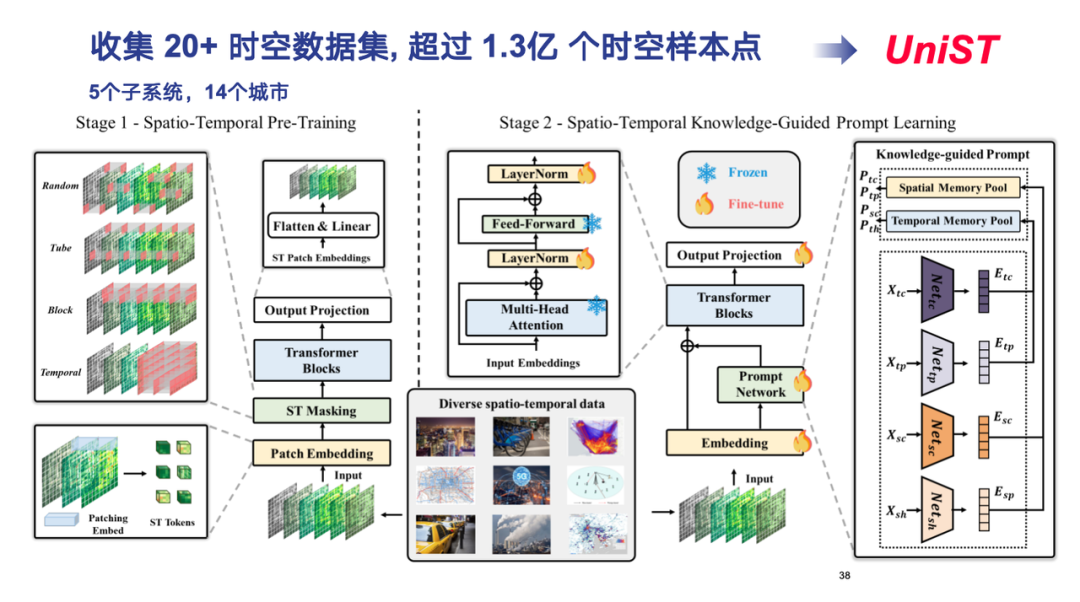
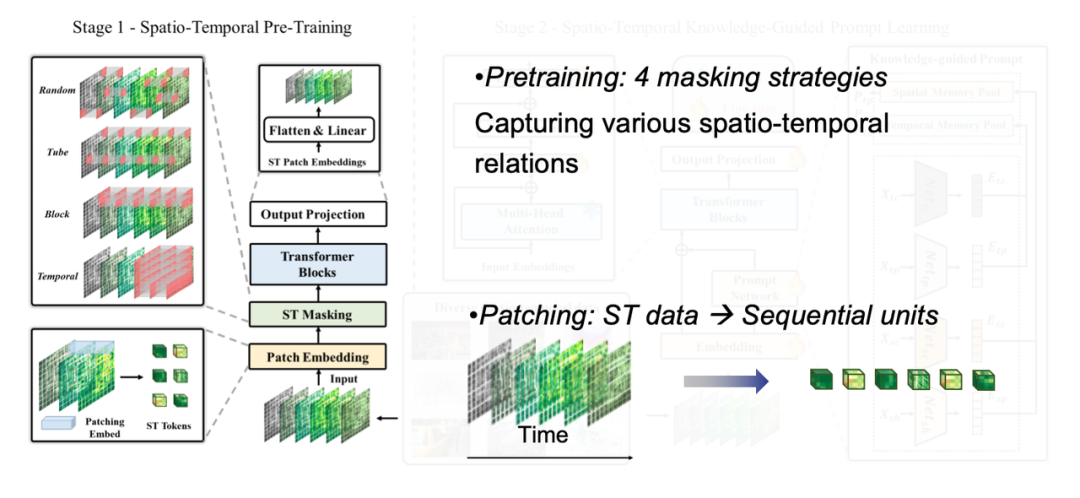
Dans la première étape de la formation du modèle,Nous tokenisons différents types de données spatio-temporelles, décomposons les tenseurs de haute dimension en petits blocs, chacun correspondant à un jeton, et utilisons différentes stratégies de masquage pour capturer diverses caractéristiques de corrélation spatio-temporelle.
Dans la deuxième étape de la formation du modèle,Nous devons explorer les lois communes derrière différentes formes de données spatio-temporelles. La « connaissance » fait ici référence aux modèles évolutifs classiques qui prévalent dans les données spatio-temporelles, tels que la proximité temporelle, la périodicité et la tendance, ainsi que la proximité spatiale et la hiérarchie. En extrayant ces connaissances du domaine spatio-temporel et en définissant les modèles correspondants, nous réduisons la dimensionnalité des données réelles en plusieurs espaces de modèles et effectuons une pré-formation sur des données massives. De cette manière, lors du traitement de nouvelles données, le modèle peut rapidement faire correspondre le modèle correspondant et obtenir une prédiction précise de petits échantillons ou même d'échantillons nuls de manière similaire à RAG.

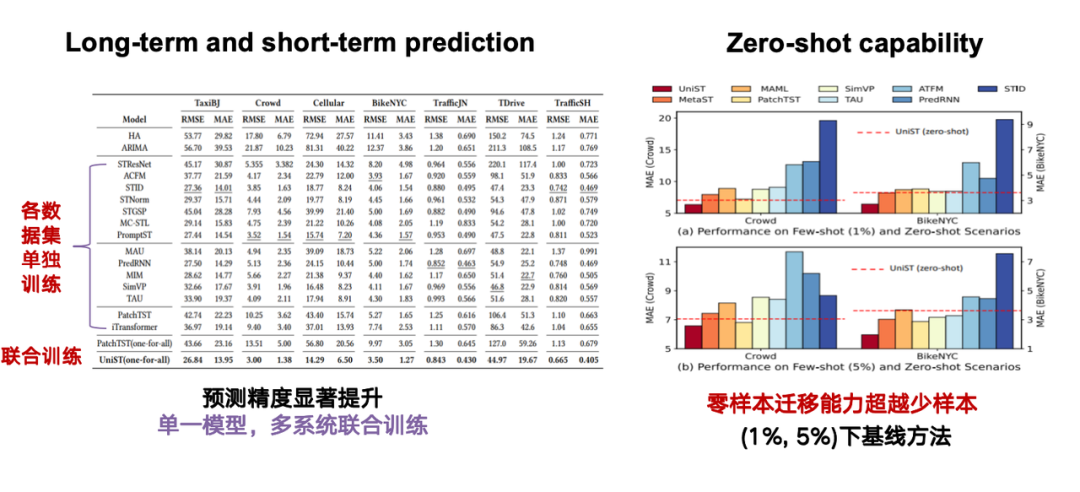
Lors de l’évaluation des performances du modèle, nous nous concentrons sur deux tâches principales : premièrement, les capacités de prédiction à long et à court terme ; deuxièmement, la capacité la plus critique, le zero-shot, qui est la capacité du modèle à gérer directement une tâche sans avoir été exposé à une tâche ou à des données spécifiques.Par exemple, si le modèle est formé sur la base d’un ensemble de données pour Pékin, alors pour les données de Shanghai qui ne sont pas incluses dans la formation, le modèle peut toujours réaliser des prédictions précises basées sur la série spatio-temporelle de Shanghai.
Comme le montre la figure ci-dessous, la ligne pointillée rouge représente l'effet de prédiction de notre méthode dans des conditions d'échantillon nul, le rectangle rouge à l'extrême gauche montre les résultats de prédiction de notre méthode dans des conditions d'échantillon 1%/5%, et les autres sont des méthodes de base. On peut constater que notre méthode surpasse considérablement la méthode de base utilisant des échantillons 1%/5% dans un transfert à zéro coup.
Pourquoi cet effet se produit-il ? En comparant la similarité des données de Pékin et de Shanghai dans la figure, nous pouvons constater que les données de l'avenue Chang'an de Pékin et du district Jing'an de Shanghai sont très similaires après un calcul rapide. Cette grande similarité explique pourquoi le modèle peut former des modèles de prédiction similaires basés sur une formation sur les données de Pékin, même s’il n’a pas été formé sur les données de Shanghai.

Nous avons également exploré le comportement des données spatio-temporelles en termes de lois d’échelle, c’est-à-dire si l’augmentation de la quantité de données améliorera considérablement les capacités du modèle. Cependant, en raison des limitations du volume et des types de données existants, nous n’avons pas encore observé d’effet d’échelle clair et nous devons enrichir davantage les types de données à cet égard.

La recherche connexe, intitulée « UniST : un modèle universel optimisé pour la prédiction spatio-temporelle urbaine », a été sélectionnée pour KDD 2024.
Adresse du document :
https://arxiv.org/abs/2402.11838
Adresse du projet open source :
https://github.com/tsinghua-fib-lab/UniST
Guidés par les connaissances physiques, de nouvelles idées sont fournies pour modéliser des systèmes urbains complexes
Enfin, je voudrais discuter des orientations futures de la modélisation des systèmes urbains complexes et des derniers progrès de mon équipe (Centre de science urbaine et de calcul, Département d'électronique, Université Tsinghua).
Nous pensons que les connaissances physiques peuvent être davantage combinées pour améliorer la robustesse et la capacité de généralisation du modèle.Pour les systèmes urbains où de nombreux mécanismes n’ont pas été entièrement explorés, nous pouvons faire un usage complet de méthodes telles que la régression symbolique et l’inférence de dynamique de réseau pour tenter d’extraire des formules symboliques qui décrivent les lois d’évolution du système à partir de données réelles.

La recherche connexe a été publiée dans ICLR 2023 sous le titre « Apprentissage de modèles symboliques pour un mécanisme physique structuré par graphes ».
Adresse du document :https://openreview.net/pdf?id=f2wN4v_2__W
Dans le domaine des réseaux complexes à grande échelle, il existe déjà des outils de réduction de dimensionnalité basés sur la théorie en physique statistique, tels que le groupe de renormalisation. Les appliquer à des prédictions réelles de réseaux à grande échelle permet d’identifier le « squelette » de faible dimension de la dynamique évolutive et de réaliser des prédictions à long terme. C’est également l’objet de nos recherches récentes.

La recherche connexe a été publiée dans KDD 2024 sous le titre « Prédire la dynamique à long terme des réseaux complexes via l'identification du squelette dans l'espace hyperbolique ».
Adresse du document :https://arxiv.org/abs/2408.09845
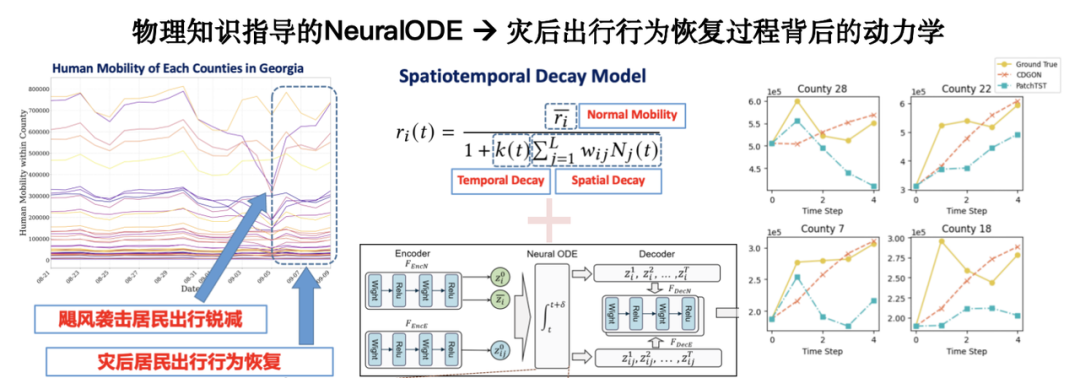
De plus, l’introduction de connaissances physiques pour soutenir l’apprentissage sur de petits échantillons améliorera considérablement la capacité de généralisation du modèle.Prenons l’exemple des interventions d’urgence après une catastrophe : il existe un manque de données historiques sur ce scénario, mais certains chercheurs ont construit des équations dynamiques du comportement humain après une catastrophe dans une perspective de mécanisme. La combinaison de ces équations avec des modèles de données réels permet des prédictions plus robustes dans le cas d’un échantillon limité.
La recherche connexe a été publiée dans KDD 2024 sous le titre « Physics-informed Neural ODE for Post-disaster Mobility Recovery ».
Adresse du document :https://dl.acm.org/doi/10.1145/3637528.3672027
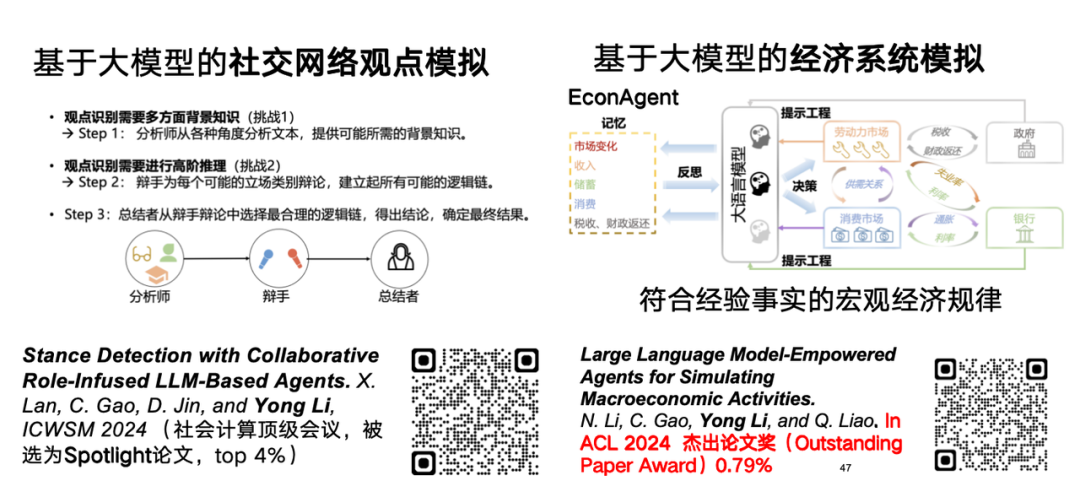
Nous pensons également que les grands modèles linguistiques ont le potentiel de raisonnement et de simulation dans le domaine des données spatio-temporelles.Par exemple, de grands modèles linguistiques peuvent être utilisés pour simuler le sentiment d’un réseau ou des systèmes économiques. Concernant la recherche sur la simulation des perspectives de réseau avec de grands modèles de langage, l'article connexe a été publié à l'ICWSM 2024 sous le titre « Stance Detection with Collaborative Role-Infused LLM-Based Agents ».
Adresse du document :https://arxiv.org/abs/2310.10467
En ce qui concerne l'étude de la simulation du modèle de langage à grande échelle des systèmes économiques, nous avons utilisé l'agent du modèle de langage à grande échelle pour simuler efficacement le modèle macroéconomique conforme aux lois empiriques.La recherche connexe, intitulée « EconAgent : agents dotés de modèles de langage de grande taille pour simuler les activités macroéconomiques », a remporté le prix ACL 2024 Outstanding Paper Award.
Adresse du document :https://arxiv.org/abs/2310.10436
Étant donné que les grands modèles linguistiques sont formés sur la base d’une grande quantité de données linguistiques générées par l’homme et possèdent des capacités de raisonnement et de prise de décision de type humain, notre équipe explore leur application dans la génération ou la simulation du comportement humain. Par rapport à l'approche traditionnelle basée sur un modèle génératif, avec l'aide de connaissances de pré-formation de modèle volumineuses, nous avons constaté que seulement 200 échantillons sont nécessaires pour obtenir des effets similaires à ceux de 100 000 échantillons de formation, permettant une généralisation rapide dans des scénarios spécifiques.
La recherche connexe « Chain-of-Planned-Behaviour Workflow Elicits Few-Shot Mobility Generation in LLMs » a été téléchargée sur le site Web de préimpression arXiv.
Adresse du document :https://arxiv.org/abs/2402.09836
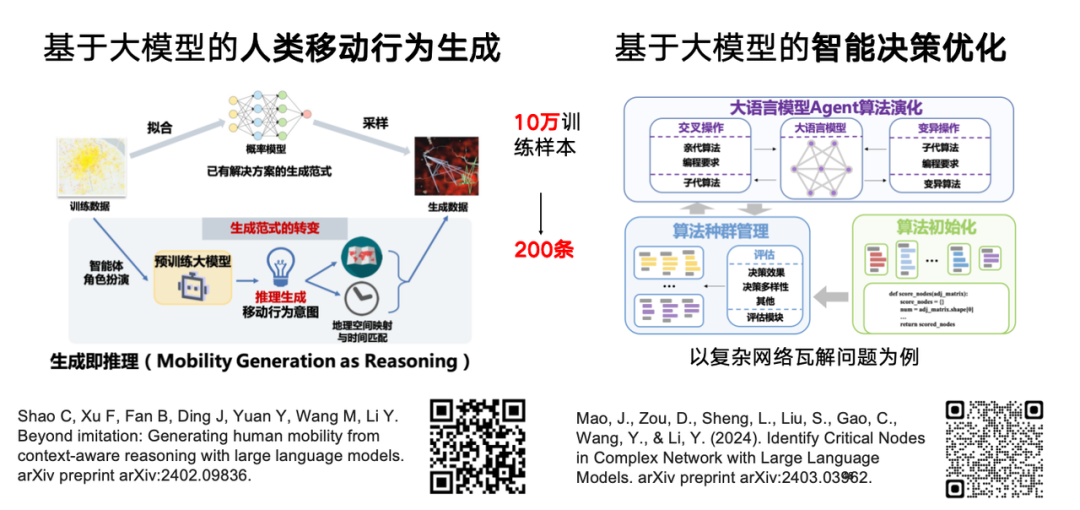
Notre équipe étudie également si les grands modèles linguistiques peuvent être davantage utilisés pour l’optimisation intelligente de la prise de décision.La recherche connexe « Identifier les nœuds critiques dans un réseau complexe avec de grands modèles de langage » a été téléchargée sur le site Web de préimpression arXiv.
Adresse du document :https://arxiv.org/abs/2403.03962
À propos de FIB LAB
L'orateur invité de cette conférence est le Dr Jingtao Ding du Centre de recherche en sciences urbaines et en informatique (FIB LAB) du Département de génie électronique de l'Université Tsinghua.Le centre de recherche se concentre sur la recherche en sciences urbaines et en informatique, prend la science urbaine comme problème de recherche fondamental, mène des recherches basées sur des théories telles que les systèmes complexes et la sociologie computationnelle, et combine la nouvelle génération d'« intelligence artificielle cognitive » de la science des données et de l'apprentissage automatique comme technologie de base pour servir les domaines d'application des jumeaux urbains, de la gouvernance urbaine, des jumeaux de réseaux sans fil et d'autres domaines d'application qui répondent aux principaux besoins nationaux. L'équipe compte actuellement 6 enseignants et plus de 60 étudiants.

L'équipe a publié plus de 150 articles universitaires dans des revues internationales de premier plan telles que les sous-revues de Nature et des conférences internationales de premier plan telles que KDD, NeurIPS, WWW et UbiComp (7 sous-revues et plus de 100 articles CCF A), avec plus de 25 000 citations. L'équipe a remporté 7 prix du meilleur article/nomination lors de conférences internationales.L'équipe a présidé ou participé à plus de 15 projets, dont le plan clé de R&D du ministère des Sciences et de la Technologie et la Fondation nationale des sciences naturelles de Chine, et les réalisations connexes ont remporté le deuxième prix du Prix national du progrès scientifique et technologique.
Le centre de recherche a toujours adhéré à l’intégration de l’industrie et du monde universitaire. Ces dernières années, elle a établi de bonnes relations de coopération avec des entreprises telles que Huawei, Tencent, Alibaba, Microsoft Research Asia, Meituan, Kuaishou, AutoNavi, SenseTime, Toyota et des opérateurs mobiles, et dispose de nombreuses opportunités de coopération d'entreprise et de stage.
Page d'accueil du laboratoire :https://fi.ee.tsinghua.edu.cn/
Page d'accueil personnelle :https://fi.ee.tsinghua.edu.cn/~dingjingtao/