Google DeepMind's New AI Approach to the Millennium Prize Aims to Discover New Unstable Singularities in Three Fluid equations.

As early as the end of May this year, mathematician Javier Gómez Serrano revealed in an interview that he was working with Google DeepMind to"Trying to solve one of the most intractable puzzles known to mankind - the Navier-Stokes equations - as quickly as possible."The equation is one of seven Millennium Prize Problems awarded by the Clay Mathematics Institute, with a $1 million prize for the solver.

It is reported that the project called "Operation Navier-Stokes" initiated by Javier Gómez Serrano and others has lasted for 3 years and is carried out by a team of 20 people, and has always been kept highly confidential. However, Demis Hassabis, head of Google DeepMind, also revealed in an interview in January this year thatHe said he was "on the verge of solving a Millennium Prize problem," but did not specify which one it was. "We'll know the answer within the next year or a year and a half."

Now, this mysterious operation seems to have gradually been unveiled.

Google DeepMind, in collaboration with researchers from New York University, Stanford University, Brown University and other institutions, has developed a machine learning framework and a high-precision Gauss-Newton optimizer.New unstable singularities were systematically discovered for the first time in three different fluid equations.A concise empirical asymptotic formula is revealed, linking the blow-up rate to the instability order.

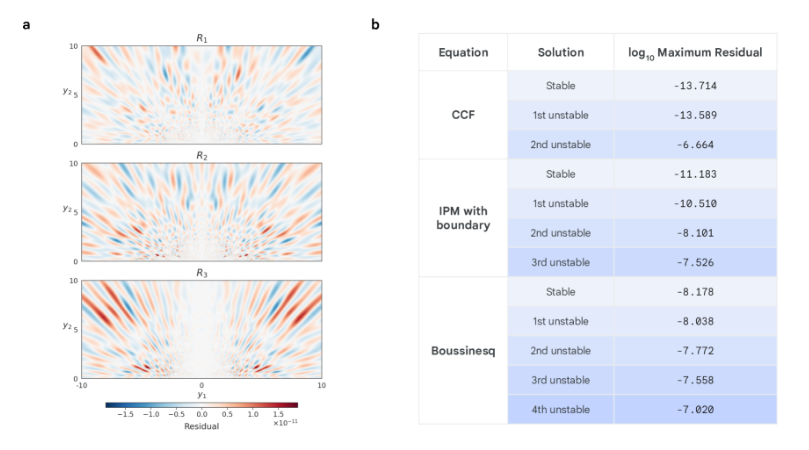
The experimental results show thatThe method achieved significantly better accuracy than existing work on all solutions found.For specific CCF solutions, the results are even close to the machine limit of double-precision floating-point, limited only by the round-off error of GPU hardware, providing a new research paradigm for exploring the complex landscape of nonlinear partial differential equations (PDEs) and opening up new paths to overcome long-standing problems in mathematical physics.

The related research is titled "Discovery of Unstable Singularities" and has been published as a preprint on arXiv.

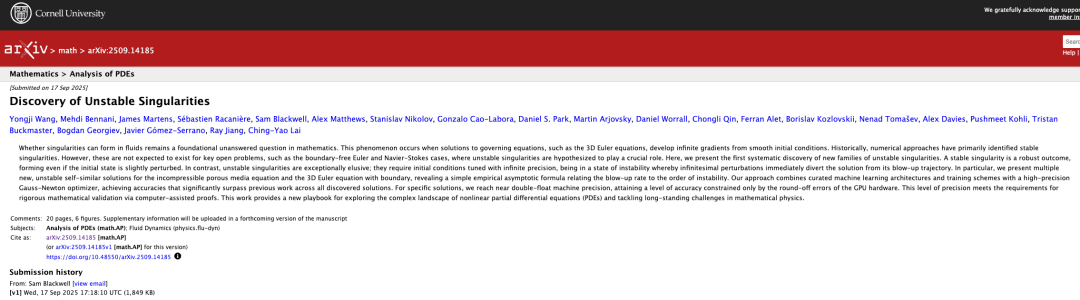
Paper address:
https://go.hyper.ai/iGh6t
Follow the official account and reply "Unstable Singularity" to download the full paper

Discover and analyze two-stage structures and find unstable singularities

Looking back at the history of human exploration of the laws of nature, fluid mechanics has always been one of the most complex and challenging fields. For centuries, mathematicians have relied on complex equations to describe the physical laws of everything from hurricane vortices to the lift of airplane wings. However, whether singularities or blow-ups will form in fluids remains one of the most fundamental and unsolved problems in mathematics. This phenomenon refers to,When the solution of the governing equations (such as the three-dimensional Euler equations) starts from smooth initial conditions, infinite gradients may evolve.

Traditional numerical methods mainly identify stable singularities, which are robust results that can be formed even with slight perturbations of the initial conditions. In contrast, unstable singularities are extremely difficult to capture, as they require the initial conditions to be adjusted to an infinitely precise degree.Because in this highly unstable state, even a small perturbation will immediately cause the solution to deviate from the blow-up trajectory.However, for some key unsolved problems—such as boundary-free Euler and Navier-Stokes cases—there is widespread speculation in the mathematical community that unstable singularities may play a crucial role.

In response to this century-long unresolved problem,The researchers went through two stages: solution discovery and solution analysis.Achieve high-precision discovery of unstable singularities.

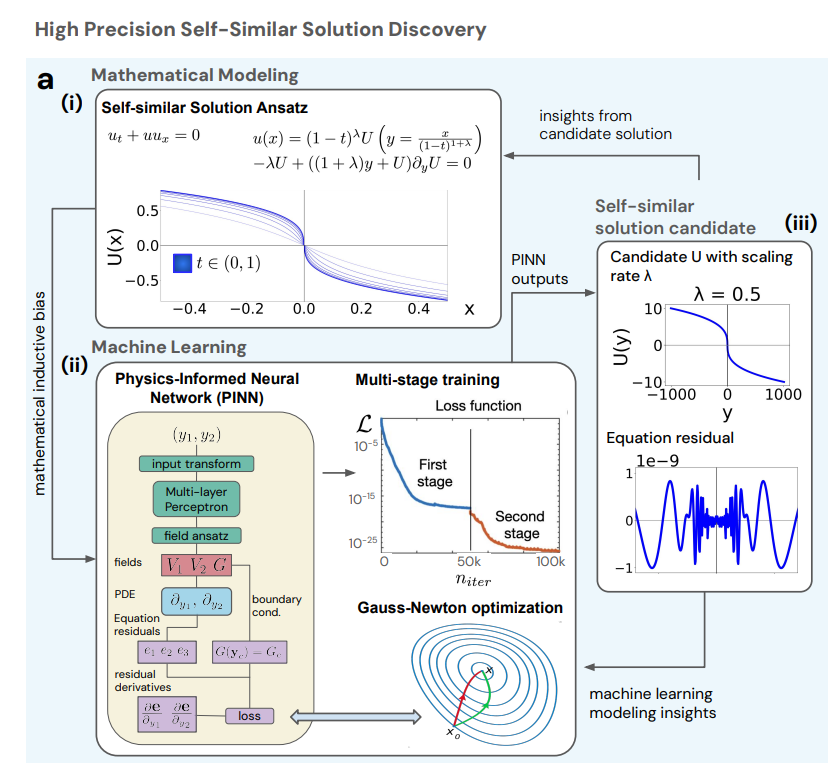
first,The researchers used a candidate solution to search for explosive solutions with a self-similar scaling factor λ and their self-similar spatial distribution, as shown in Figure (i) below, for the Burgers equation. They then used an iterative approach to continuously optimize the machine learning process and the accuracy of the solution (shown in Figure ii below). The empirical results and accuracy of the candidate solution guided mathematical modeling and neural network architecture design, which in turn guided the inductive biases in the network architecture, such as the input coordinate transformation and the morphological design of the output field.

In this process, the researchers used a physical information neural network (PINN), combined with a Gauss-Newton optimizer and a multi-stage training strategy, to generate high-precision candidate solutions while finding the correct scaling rate λ.

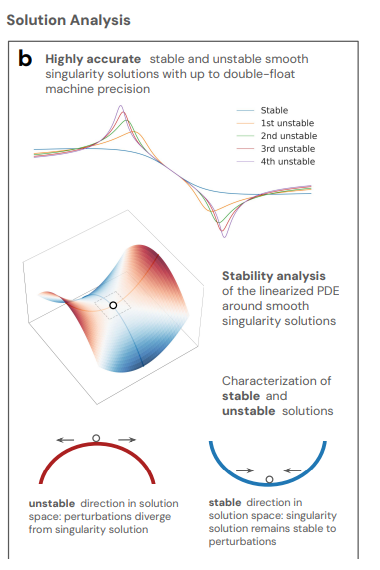
Secondly,During the analysis of solutions, for each unstable solution found for the CCF, IPM, and Boussinesq equations, the researchers analyzed its stability by linearizing the partial differential equations around it. For each nth unstable solution found, the researchers found n unstable modes that share the same symmetry assumptions as the solution.

These unstable modes indicate directions in which to push the solution toward greater stability, demonstrating that the family of solutions discovered is complete within the range of permissible values of λ considered. This allows the researchers to characterize not only the degree of stability but also the discovery of stable and unstable singularities with high precision.

Mathematical insights + neural networks make PINN a new weapon

In this study, physical information neural networks were given new power, going beyond their typical role as a general tool for solving partial differential equations. The research team represented the solution as a smooth function parameterized by the neural network.Enables mathematical insights to be embedded directly into neural network architectures, guiding the optimization process towards mathematically relevant solutions.

The research team used architectural design to enforce constraints derived from the governing equations, such as symmetry, periodicity, and handling of infinite domains, providing a robust standard training parameter for learning. By iteratively optimizing the network architecture through a feedback loop of numerical experiments and mathematical analysis, they explicitly factored this behavior and rewrote the remaining equations, significantly improving optimization stability.

Improved high-precision training

In order to meet the extremely high accuracy required for unstable singularities, the researchers made two key improvements to the training process.The Gauss-Newton optimizer and multi-stage training are introduced for high-precision training.

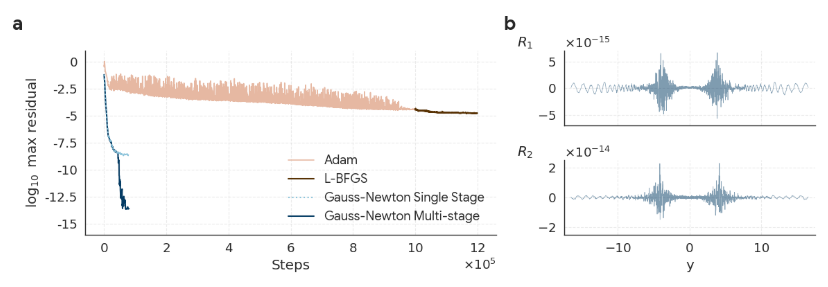
The reason for adopting this optimizer is that currently common standard gradient optimizers (such as Adam or L-BFGS) are insufficient to produce high-quality solutions to the equation. Therefore, the research team chose the more powerful Gauss–Newton optimization method to optimize the neural network. Due to the small size of the network, this previously unfeasible solution was successful. Experimental results show that Gauss–Newton can reduce the residual error to 10⁻⁸ in approximately 50,000 iterations.It shows better performance and significantly faster convergence than the standard gradient optimizer.

in short,The idea of multi-stage training is to first train one network to get an approximate solution, and then train a second network to specifically correct the errors that the previous network did not handle well.Combining the outputs of the two networks can push the solution to higher accuracy. In experiments on stable solutions and first-order unstable solutions of the CCF and IPM equations, the multi-stage training method was able to improve the maximum residual by five orders of magnitude, an accuracy sufficient to meet the rigorous mathematical verification based on CAP.

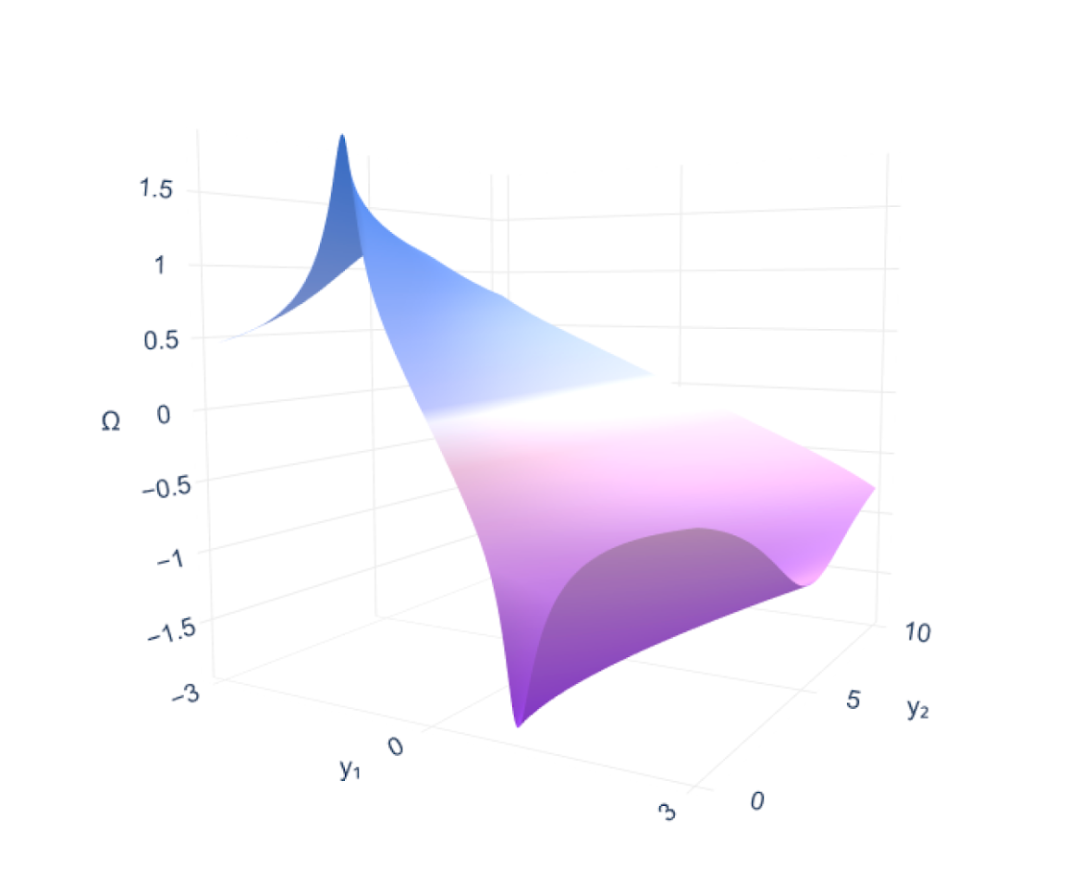
This approach enables the model to achieve a new level of accuracy. Using three-dimensional visualization and analysis of two-dimensional vorticity fields as reference examples, the research team demonstrated a measurement of the degree of rotation of the fluid at each point. The maximum error resolved is equivalent to improving the prediction accuracy of the Earth's diameter to within a few centimeters.

Paper 1 As a Chinese Ph.D.

Yongji Wang, the paper's lead author, is currently a postdoctoral fellow at the Courant Institute of Mathematical Sciences at New York University and a visiting postdoctoral fellow at Stanford University. His research interests include continuum mechanics, geophysics, and scientific machine learning, and he has extensive experience applying theoretical and numerical techniques to elucidate complex physical processes in nature and the environment.

The research focuses on developing high-precision deep learning techniques for a variety of scientific problems, ranging from revealing the hidden physical properties of Antarctic ice shelves to finding self-similar explosive solutions to nonlinear partial differential equations (PDEs).

References:
1.https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/
2.https://english.elpais.com/science-tech/2025-06-24/spanish-mathematician-javier-gomez-serrano-and-google-deepmind-team-up-to-solve-the-navier-stokes-million-dollar-problem.html

3.https://mp.weixin.qq.com/s/CRlGLmji4BWNkNaA7e2JEw