يهدف نهج الذكاء الاصطناعي الجديد من Google DeepMind لجائزة الألفية إلى اكتشاف تفردات غير مستقرة جديدة في ثلاث معادلات سائلة.

في وقت مبكر من نهاية شهر مايو/أيار من هذا العام، كشف عالم الرياضيات خافيير جوميز سيرانو في مقابلة أنه كان يعمل مع Google DeepMind لـ"محاولة حل واحدة من أكثر الألغاز صعوبة التي عرفتها البشرية - معادلات نافييه-ستوكس - في أسرع وقت ممكن."المعادلة هي واحدة من سبع مسائل جائزة الألفية التي يمنحها معهد كلاي للرياضيات، مع جائزة قدرها مليون دولار لمن يحلها.

يُقال إن مشروع "عملية نافيير-ستوكس"، الذي أطلقه خافيير غوميز سيرانو وآخرون، استمر لمدة ثلاث سنوات، وينفذه فريق من عشرين شخصًا، وقد ظل سريًا للغاية. مع ذلك، كشف ديميس هاسابيس، رئيس شركة جوجل ديب مايند، في مقابلة أجريت معه في يناير من هذا العام أنقال إنه "على وشك حل مسألة جائزة الألفية"، لكنه لم يحدد أي مسألة هي. "سنعرف الإجابة خلال العام أو العام ونصف العام القادمين".

والآن يبدو أن هذه العملية الغامضة بدأت تتكشف تدريجيا.

قامت شركة Google DeepMind، بالتعاون مع باحثين من جامعة نيويورك وجامعة ستانفورد وجامعة براون ومؤسسات أخرى، بتطوير إطار عمل للتعلم الآلي ومحسن Gauss-Newton عالي الدقة.تم اكتشاف تفردات غير مستقرة جديدة بشكل منهجي لأول مرة في ثلاث معادلات سوائل مختلفة.تم الكشف عن صيغة تجريبية موجزة تربط معدل الانفجار بترتيب عدم الاستقرار.

وتظهر النتائج التجريبية أنوقد حققت هذه الطريقة دقة أفضل بكثير من العمل الموجود على جميع الحلول التي تم العثور عليها.بالنسبة لحلول CCF المحددة، فإن النتائج قريبة حتى من حد الآلة للفاصلة العائمة ذات الدقة المزدوجة، محدودة فقط بخطأ التقريب في أجهزة وحدة معالجة الرسومات، مما يوفر نموذج بحث جديد لاستكشاف المشهد المعقد للمعادلات التفاضلية الجزئية غير الخطية (PDEs) وفتح مسارات جديدة للتغلب على المشاكل الطويلة الأمد في الفيزياء الرياضية.

البحث ذو الصلة يحمل عنوان "اكتشاف التفردات غير المستقرة" وقد تم نشره كنسخة أولية على arXiv.

عنوان الورقة:
https://go.hyper.ai/iGh6t
اتبع الحساب الرسمي ورد على "التفرد غير المستقر" لتحميل الورقة كاملة

اكتشاف وتحليل الهياكل المكونة من مرحلتين والعثور على المفردات غير المستقرة

بالنظر إلى تاريخ استكشاف الإنسان لقوانين الطبيعة، لطالما كانت ميكانيكا الموائع من أكثر المجالات تعقيدًا وصعوبة. فعلى مدى قرون، اعتمد علماء الرياضيات على معادلات معقدة لوصف القوانين الفيزيائية لكل شيء، من دوامات الأعاصير إلى رفع أجنحة الطائرات. ومع ذلك، يبقى نشوء التفردات أو الانفجارات في الموائع من أكثر المسائل جوهريةً وغير محلولة في الرياضيات. تشير هذه الظاهرة إلى:عندما يبدأ حل المعادلات الحاكمة (مثل معادلات أويلر ثلاثية الأبعاد) من ظروف أولية سلسة، فقد تتطور تدرجات لا نهائية.

تعتمد الطرق العددية التقليدية بشكل أساسي على تحديد التفردات المستقرة، وهي نتائج متينة يمكن الحصول عليها حتى مع وجود اضطرابات طفيفة في الظروف الابتدائية. في المقابل، يصعب للغاية رصد التفردات غير المستقرة، إذ تتطلب ضبط الظروف الابتدائية بدقة متناهية.لأنه في هذه الحالة غير المستقرة للغاية، حتى الاضطراب الصغير سوف يتسبب على الفور في انحراف الحل عن مسار الانفجار.ومع ذلك، بالنسبة لبعض المشاكل الرئيسية التي لم يتم حلها بعد - مثل حالات أويلر ونافير-ستوكس الخالية من الحدود - هناك تكهنات واسعة النطاق في المجتمع الرياضي بأن التفردات غير المستقرة قد تلعب دورا حاسما.

ردًا على هذه المشكلة التي لم يتم حلها منذ قرن من الزمان،لقد مر الباحثون بمرحلتين: اكتشاف الحل وتحليل الحل.تحقيق اكتشاف عالي الدقة للتفردات غير المستقرة.

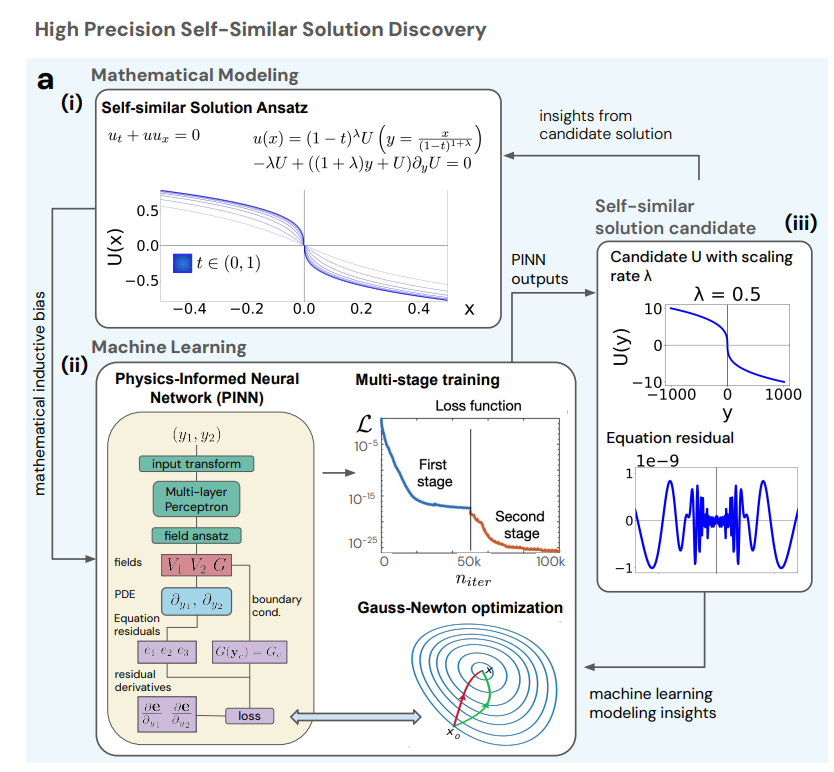
أولاً،استخدم الباحثون حلاً مرشحاً للبحث عن حلول متفجرة ذات معامل مقياس ذاتي التشابه λ وتوزيع مكاني ذاتي التشابه، كما هو موضح في الشكل (i) أدناه، لمعادلة برجر. ثم استخدموا نهجاً تكرارياً لتحسين عملية التعلم الآلي ودقة الحل باستمرار (كما هو موضح في الشكل ii أدناه). وقد وجهت النتائج التجريبية ودقة الحل المرشح النمذجة الرياضية وتصميم بنية الشبكة العصبية، والتي بدورها وجهت التحيزات الاستقرائية في بنية الشبكة، مثل تحويل إحداثيات المدخلات والتصميم المورفولوجي لحقل المخرجات.

في هذه العملية، استخدم الباحثون شبكة عصبية للمعلومات الفيزيائية (PINN)، مقترنة بمحسن Gauss-Newton واستراتيجية تدريب متعددة المراحل، لتوليد حلول مرشحة عالية الدقة مع العثور على معدل التوسع الصحيح λ.

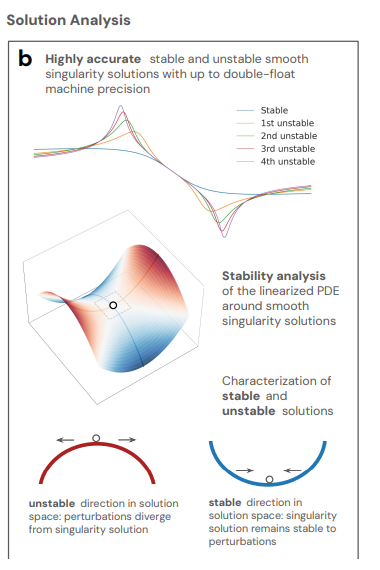
ثانيًا،أثناء تحليل الحلول، لكل حل غير مستقر وُجد لمعادلات CCF وIPM وBoussinesq، حلل الباحثون استقراره من خلال خطية معادلات التفاضل الجزئي المحيطة به. لكل حل غير مستقر رقم n، وجد الباحثون n نمطًا غير مستقر يشترك في نفس افتراضات التماثل مع الحل.

تشير هذه الأنماط غير المستقرة إلى اتجاهات دفع الحل نحو استقرار أكبر، مما يُظهر اكتمال مجموعة الحلول المُكتشفة ضمن نطاق قيم λ المسموح بها. وهذا يُمكّن الباحثين من تحديد درجة الاستقرار بدقة عالية، بالإضافة إلى اكتشاف التفردات المستقرة وغير المستقرة.

الرؤى الرياضية + الشبكات العصبية تجعل PINN سلاحًا جديدًا

في هذه الدراسة، مُنحت شبكات المعلومات العصبية الفيزيائية قوةً جديدة، متجاوزةً بذلك دورها التقليدي كأداة عامة لحل المعادلات التفاضلية الجزئية. قدّم فريق البحث الحل كدالة سلسة مُعَلَّمة بواسطة الشبكة العصبية.يتيح دمج الرؤى الرياضية مباشرة في هياكل الشبكات العصبية، مما يوجه عملية التحسين نحو حلول ذات صلة رياضيا.

استخدم فريق البحث التصميم المعماري لتطبيق القيود المستمدة من المعادلات الحاكمة، مثل التناظر، والدورية، ومعالجة المجالات اللانهائية، مما وفر معيارًا تدريبيًا قياسيًا قويًا للتعلم. ومن خلال التحسين التكراري لبنية الشبكة من خلال حلقة تغذية راجعة من التجارب العددية والتحليل الرياضي، قاموا بتحليل هذا السلوك بدقة وإعادة كتابة المعادلات المتبقية، مما أدى إلى تحسين استقرار التحسين بشكل ملحوظ.

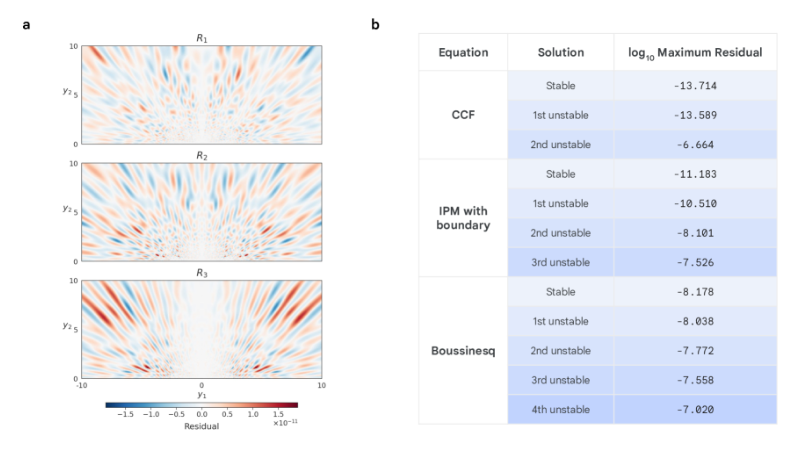
تحسين التدريب عالي الدقة

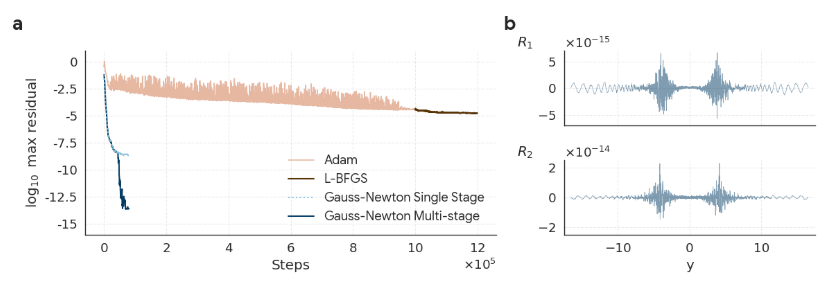
من أجل تلبية الدقة العالية للغاية المطلوبة للتفردات غير المستقرة، أجرى الباحثون تحسينين رئيسيين لعملية التدريب.تم تقديم محسن Gauss-Newton والتدريب متعدد المراحل للتدريب عالي الدقة.

يعود سبب اعتماد هذا المُحسِّن إلى أن مُحسِّنات التدرج القياسية الشائعة حاليًا (مثل Adam أو L-BFGS) غير كافية لإنتاج حلول عالية الجودة للمعادلة. لذلك، اختار فريق البحث طريقة تحسين غاوس-نيوتن الأكثر فعالية لتحسين الشبكة العصبية. ونظرًا لصغر حجم الشبكة، نجح هذا الحل الذي كان غير عملي سابقًا. تُظهر النتائج التجريبية أن طريقة غاوس-نيوتن قادرة على تقليل الخطأ المتبقي إلى 10⁻⁸ في حوالي 50,000 تكرار.إنه يظهر أداءً أفضل وتقاربًا أسرع بكثير من مُحسِّن التدرج القياسي.

باختصار،الفكرة وراء التدريب متعدد المراحل هي تدريب شبكة واحدة أولاً للحصول على حل تقريبي، ثم تدريب شبكة ثانية لتصحيح الأخطاء التي لم تتعامل معها الشبكة السابقة بشكل جيد.يمكن لدمج مخرجات الشبكتين رفع دقة الحل. في التجارب التي أُجريت على الحلول المستقرة والحلول غير المستقرة من الدرجة الأولى لمعادلات CCF وIPM، استطاعت طريقة التدريب متعدد المراحل تحسين الحد الأقصى المتبقي بخمسة أوامر من حيث الحجم، وهي دقة كافية لتلبية متطلبات التحقق الرياضي الدقيق القائم على CAP.

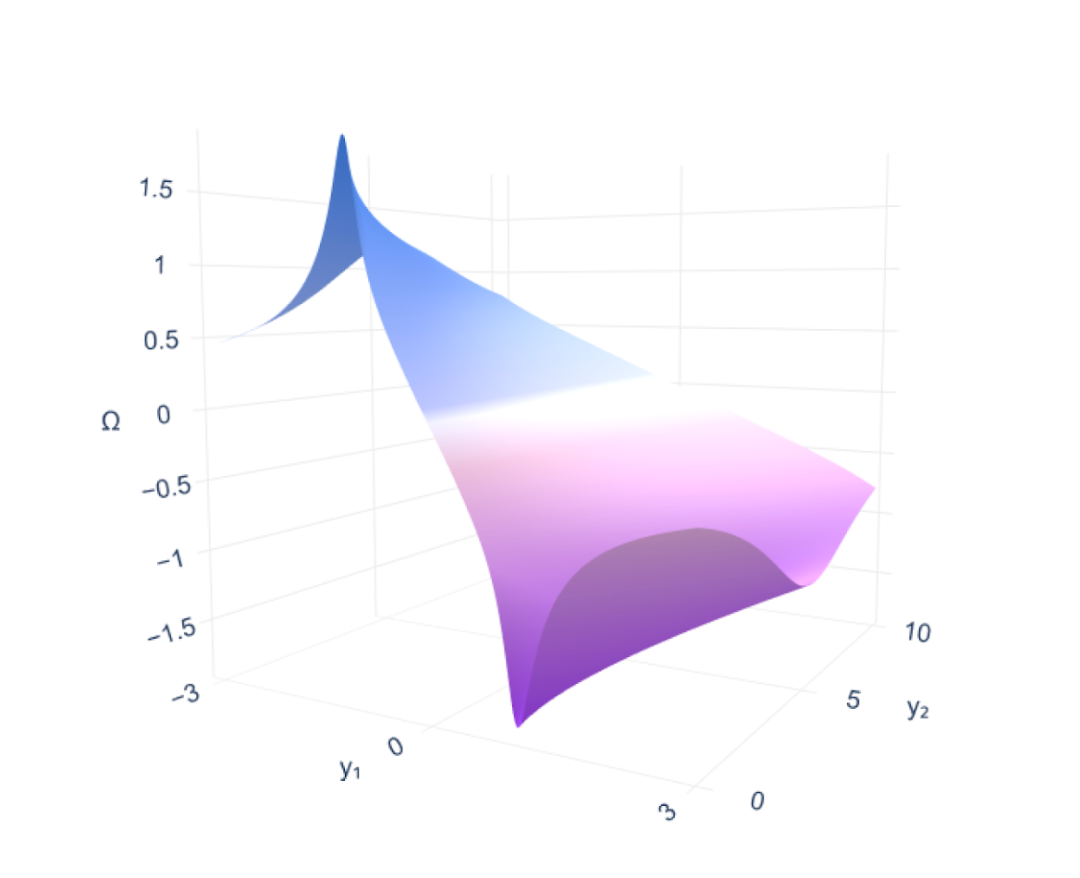
يُمكّن هذا النهج النموذج من تحقيق مستوى جديد من الدقة. باستخدام التصور ثلاثي الأبعاد وتحليل حقول الدوامات ثنائية الأبعاد كأمثلة مرجعية، أظهر فريق البحث قياسًا لدرجة دوران السائل عند كل نقطة. يُعادل الحد الأقصى للخطأ المُحَلّ تحسين دقة التنبؤ بقطر الأرض إلى بضعة سنتيمترات.

الورقة 1 كطالب دكتوراه صيني

يونغجي وانغ، المؤلف الرئيسي للورقة البحثية، هو حاليًا زميل ما بعد الدكتوراه في معهد كورانت للعلوم الرياضية بجامعة نيويورك، وزميل ما بعد الدكتوراه زائر في جامعة ستانفورد. تشمل اهتماماته البحثية ميكانيكا الاستمرارية، والجيوفيزياء، والتعلم الآلي العلمي، ولديه خبرة واسعة في تطبيق التقنيات النظرية والعددية لتوضيح العمليات الفيزيائية المعقدة في الطبيعة والبيئة.

يركز البحث على تطوير تقنيات التعلم العميق عالية الدقة لمجموعة متنوعة من المشاكل العلمية، بدءًا من الكشف عن الخصائص الفيزيائية المخفية لجرف الجليد في القارة القطبية الجنوبية إلى إيجاد حلول انفجارية متشابهة ذاتيًا لمعادلات التفاضل الجزئي غير الخطية (PDEs).

مراجع:
1.https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/
2.https://english.elpais.com/science-tech/2025-06-24/spanish-mathematician-javier-gomez-serrano-and-google-deepmind-team-up-to-solve-the-navier-stokes-million-dollar-problem.html

3.https://mp.weixin.qq.com/s/CRlGLmji4BWNkNaA7e2JEw