Command Palette
Search for a command to run...
Prediction Accuracy Can Be Improved by 60%, and the Innovative Neural Symbolic Regression Method Can Automatically Derive high-precision Network Dynamics formulas.

In the study of complex systems, "networks" are almost ubiquitous—from gene regulatory networks and microbial communities to communication and transportation networks in human society. However, truly understanding the dynamics behind these high-dimensional networks remains one of the most challenging problems in the field.
on the one hand,The development of sensors, sequencing technologies, and digital infrastructure has enabled people to have access to an unprecedented amount of observational data;on the other hand,Explainable mathematical models capable of explaining these data and revealing causal mechanisms are severely lacking. High dimensionality, strong nonlinearity, and structural heterogeneity mean that traditional modeling methods either rely on strong assumptions and have limited applicability, or can only remain at the level of correlation analysis, failing to grasp the essential laws governing system operation.
In response to the relevant challenges,Professor Li Yong and his team from the Department of Electronic Engineering at Tsinghua University proposed a neural symbolic regression method, ND².This method characterizes system dynamics by automatically deriving mathematical formulas from data. It simplifies the search problem on high-dimensional networks to a one-dimensional system and utilizes pre-trained neural networks to guide high-precision formula discovery. In studies of infectious disease transmission on human mobility networks at different scales, this method has revealed node correlation dynamics exhibiting the same power-law distribution across scales and disclosed differences in intervention effectiveness across countries.
The related research, titled "Discovering network dynamics with neural symbolic regression," has been published in Nature Computational Science.

Paper link:
https://www.nature.com/articles/s43588-025-00893-8
Follow our official WeChat account and reply "neural symbolic regression" in the background to download the complete PDF.
More AI frontier papers:
https://hyper.ai/papers
A symbol search algorithm guided by NDformer is introduced to achieve efficient formula discovery.
Researchers have proposed a neural symbolic regression method (Neural Discovery of Network Dynamics, ND²), a deep learning approach that automatically discovers network dynamics formulas through symbolic regression. To this end,Researchers designed a set of network dynamical operators.This transforms the symbol search problem, originally on high-dimensional networks, into an equivalent one-dimensional problem; simultaneously...A symbolic search algorithm guided by NDformer is introduced.To achieve efficient formula discovery.
As shown in the figure below, network dynamics operators include source operator φ(s), target operator φ(t), and aggregation operator ρ. These operators make the expression of network dynamics formula independent of network size, thereby compressing the search space that originally grows exponentially with network size into a dimension-independent one-dimensional problem.
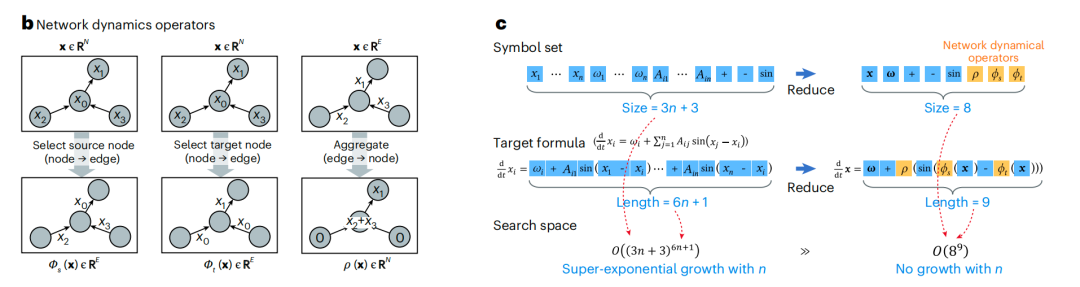
Furthermore, the symbolic search algorithm guided by NDformer significantly improves the efficiency and accuracy of formula discovery by combining the advantages of neural networks and symbolic search methods.The algorithm consists of a symbolic module responsible for searching and a neural module responsible for guidance.As shown in the figure below, the neural module NDformer learns to capture the implicit features of the system's underlying dynamics and estimates the probability distribution of each symbol required to construct the formula; the symbol module MCTS selects symbols based on the probabilities predicted by NDformer, thereby constructing candidate formulas.
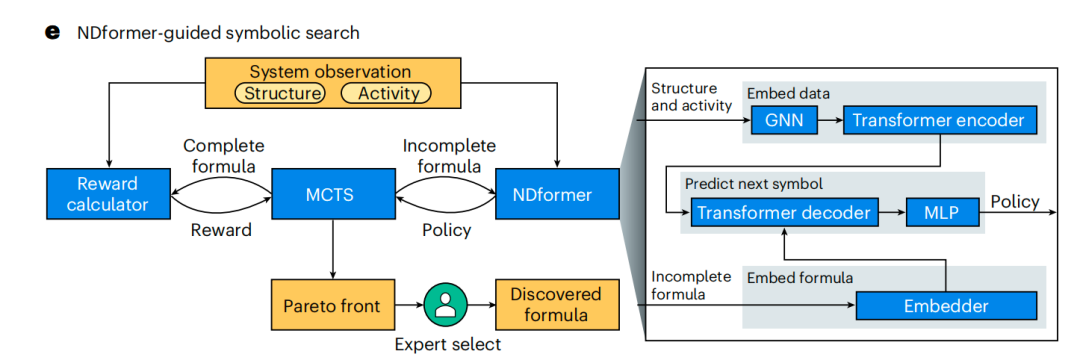
For each candidate formula, the reward calculator uses the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to fit the unknown coefficients (if any) to the data and returns a reward value that comprehensively evaluates accuracy and simplicity. Candidate formulas that fit the data better and are shorter receive higher rewards, thus guiding MCTS to continuously generate better candidate formulas.
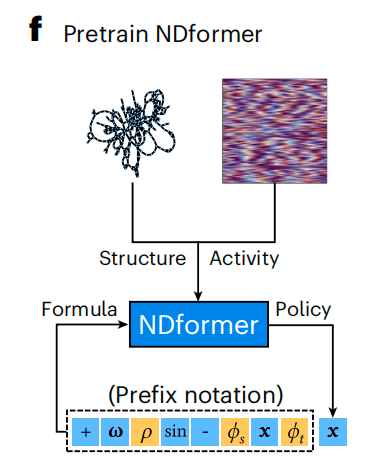
Specifically,NDformer is a type of neural network that combines graph neural networks (GNNs) and transformers.Used to capture complex network dynamics features. NDformer learns to predict the signs in the formula given the network structure and node activity data through pre-training, and further guides the Monte Carlo Tree Search (MCTS) module to efficiently explore the search space, ultimately discovering an accurate and concise network dynamics formula.
Revealing the microscopic dynamics of "emergence" phenomena in complex multi-scale and multidisciplinary systems.
To verify the effectiveness of the neural symbolic regression method, the research team applied the neural symbolic regression method ND² to complex systems at multiple scales and in different fields, from the cellular scale to the urban scale, spanning genetic, ecological and social networks, to explore the microscopic dynamics behind different complex systems, as shown in the figure below.

In gene expression networks,The dynamic formula discovered by the research team improves prediction accuracy by approximately 60% compared to existing empirical formulas.More importantly, the discovered formula reveals higher-order interactions: the mutual regulation between two genes is not only influenced by the two genes themselves, but also by a third gene, thus exhibiting a complex microscopic dynamic structure.
In the microbial ecosystem,The discovered dynamic formula improves prediction accuracy by approximately 561 TP3T compared to the traditional Lotka-Volterra model.It also exhibits unique behaviors not yet seen in existing models: populations with a larger number of individuals are less affected by other populations.
Meanwhile, researchers also applied the ND² symbolic regression method to discover the transmission mechanisms of infectious diseases in urban systems at different scales. The study selected seven representative regions, covering transmission networks from city-level to global scales, and automatically discovered the dynamic equations of epidemic transmission using this method, as shown in the figure below.
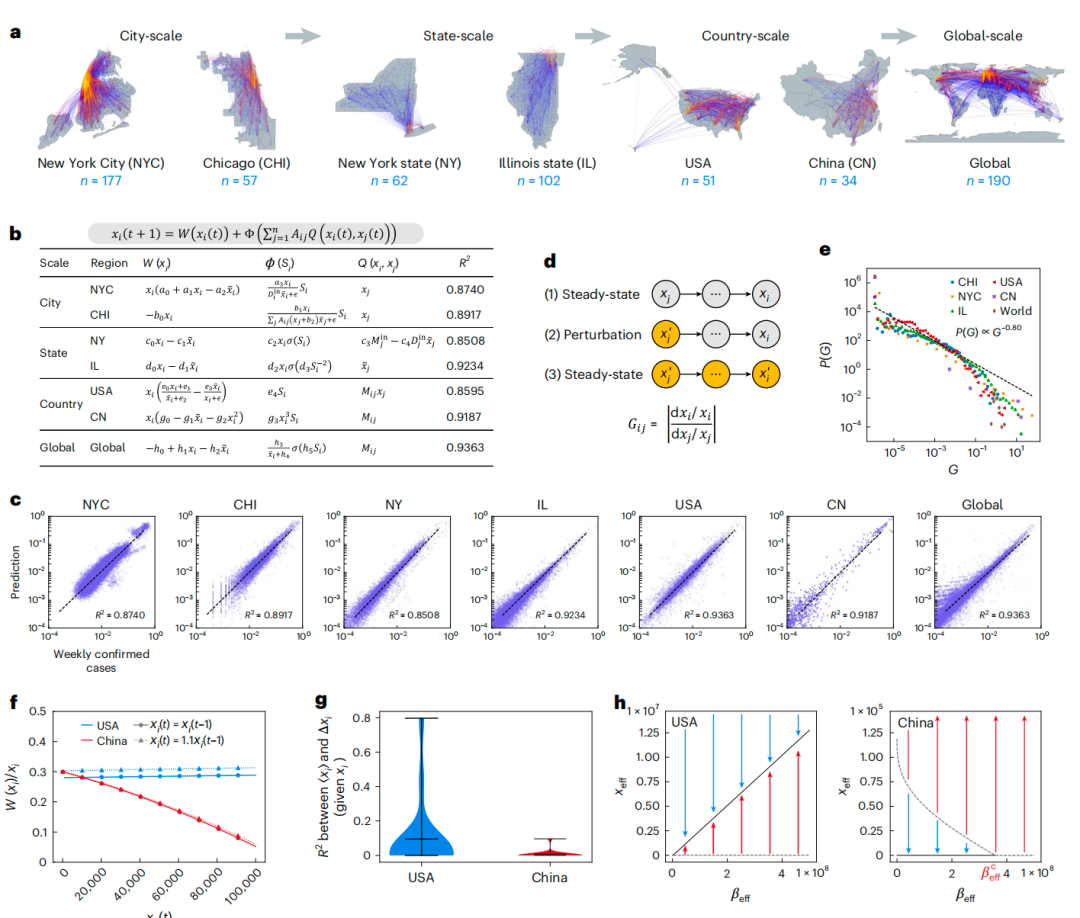
These equations demonstrate high accuracy in prediction and reveal differences in propagation mechanisms across different regions.Taking the United States and China as examples, their self-evolutionary dynamics exhibit different characteristics: in the United States, the transmission process remains stable; while in China, the intensity of transmission weakens as the number of infections increases, demonstrating a self-suppression mechanism and reflecting the effectiveness of prevention and control policies. Regarding inter-regional interaction dynamics, the number of new infections in each US state depends on the new cases in other states, indicating that interstate travel promotes the spread of the epidemic; while in China, the transmission links between provinces are extremely weak, indicating that cross-regional transmission is strictly controlled. These differences are highly consistent with the different intensities of the two countries' prevention and control strategies.
Based on the discovered dynamic equations, researchers further analyzed the macroscopic steady-state characteristics of the system. The results show that the spread of the epidemic in China and the United States exhibits drastically different patterns: In China, when inter-provincial traffic flow is below a threshold, the number of infections can be controlled for a long period; once the threshold is exceeded, the number of infections surges rapidly, exhibiting typical critical behavior; while in the United States, the average number of infections increases linearly with interstate traffic flow, indicating that traffic control has a relatively mild impact on overall transmission. This study not only reveals the dynamic root of the differences in epidemic prevention and control between the two countries,It also demonstrates the broad potential of the neural symbolic regression method to extract the microscopic mechanisms behind the cross-scale "emergence" of complex systems.
Through cross-scale and multidisciplinary validation, the research team not only proved the effectiveness of the neural symbolic regression method, but also demonstrated its potential in revealing the microscopic dynamics of complex systems and discovering new scientific knowledge, providing new tools and ideas for basic scientific research and scientific discovery.
About the team
The Center for Urban Science and Computing (FIB LAB) in the Department of Electronic Engineering at Tsinghua University conducts research at the forefront of artificial intelligence and data science. It focuses on key technological innovations in fundamental models, AI scientists, and world models, exploring the use of machine learning to model, generate, simulate, and control complex systems across scales. Research objects encompass robots, drones, and human behavior in indoor and open environments, connecting the physical space, the digital world, and social systems. The laboratory focuses on applications such as embodied intelligence, urban science, and social computing, emphasizing multidisciplinary integration and large-scale system modeling capabilities to serve the significant needs of related fields.