一句话总结

来自上海交通大学、清华大学、新加坡国立大学、微软和香港浸会大学的研究人员提出了 Qute，这是一种将 SQL 编译为高效量子电路的量子数据库，通过混合优化和选择性索引，在真实硬件上超越经典系统，推动量子原生数据管理的发展。

主要贡献

• Qute 引入了一种量子原生数据库架构，可将扩展 SQL 编译为门高效的量子电路，使量子计算成为第一类执行载体，而非基于仿真的加速器。
• 它包含一个混合优化器，可动态选择量子与经典执行计划，并采用选择性量子索引处理量子比特约束，同时使用保真度存储机制，在量子噪声下保持数据可用性。
• 在真实量子处理器 origin_wukong 上部署后，Qute 在大规模场景下展现出相对于经典基线的可测量性能优势，验证了其实用可行性，并开源了原型供社区使用。

引言

作者将量子计算作为数据库系统中的第一类执行载体，旨在通过将 SQL 操作符映射为量子电路并使用如 Grover 搜索等算法来加速全表扫描等工作负载。以往方法要么在经典硬件上模拟量子执行，要么将量子计算视为孤立加速器，缺乏端到端集成，且未能解决量子特有的约束，如噪声、量子比特限制和保真度损失。Qute 的主要贡献是一种统一架构，可将扩展 SQL 编译为门高效的量子电路，采用混合优化器动态选择量子或经典执行路径，引入选择性量子索引以减少量子比特使用，并设计保真度存储机制以在当前硬件限制下维持数据可用性。

方法

作者利用混合量子-经典架构，在量子硬件上高效执行关系操作，同时保持正确性并适应硬件约束。系统 Qute 围绕三个核心组件构建：量子感知查询引擎、针对量子数据格式优化的存储引擎，以及能动态选择量子或经典执行路径的保真度感知优化器。

查询引擎从量子感知解析器开始，将 SQL 操作符分类为精确、统计或近似类别。然后通过模块化操作符编译器将其编译为量子电路，为过滤、连接和聚合生成门高效的实现。编译器采用三层中间表示——逻辑层、量子扩展层和物理电路层——逐步将声明式查询降低为可执行的量子电路。如下图所示，查询优化器使用保真度感知成本模型，通过元组 $(T_q, P_q, \varepsilon_q)$(Tq​,Pq​,εq​) 评估每个量子操作符，捕获延迟、成功概率和近似误差。这支持混合计划生成，其中量子和经典实现的操作符均嵌入执行计划中，允许根据观测到的硬件条件在运行时自适应调整。

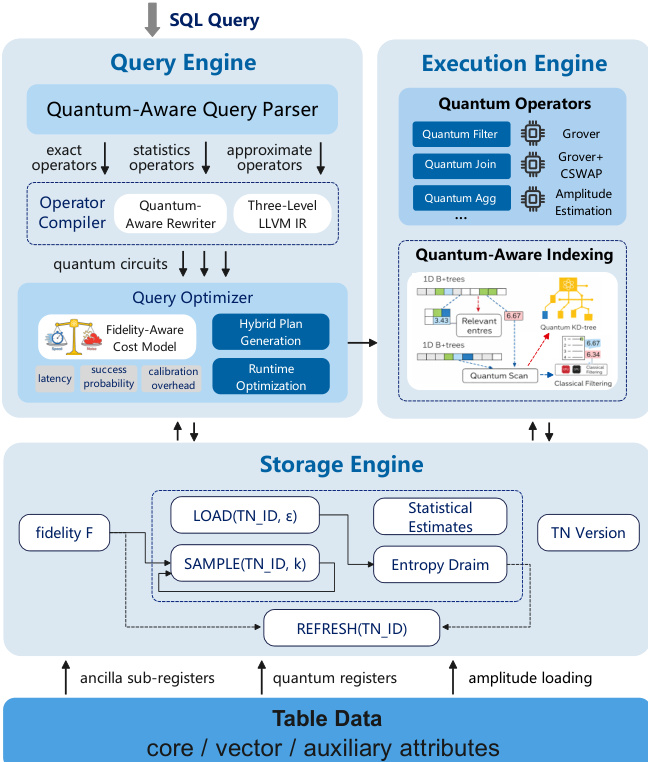
存储引擎采用以状态为中心的设计，将量子活跃属性存储为压缩张量网络（TN），支持在保真度约束下进行有界重建和采样。核心数据使用三种编码方案：基编码用于行标识符，振幅编码用于数值向量，控制编码用于存储在辅助量子比特中的元数据标志。引擎暴露保真度感知原语，如 LOAD(TN_ID, ϵ)、SAMPLE(TN_ID, k) 和 REFRESH(TN_ID)，以管理访问过程中的熵和噪声。经典元数据单独维护以确保可恢复性。

对于量子加速操作符，Qute 将经典数据库原语重构为利用振幅级并行性的量子电路。对于过滤，它改编了 Grover 算法：行标识符映射到搜索空间，谓词被编译为标记满足行的预言机 $O_\phi$Oϕ​，通过相位反转实现。复合谓词使用辅助量子比特的多控制门实现。Grover 迭代放大匹配行的振幅后，经典协调确保正确性，通过去重和重新验证结果。

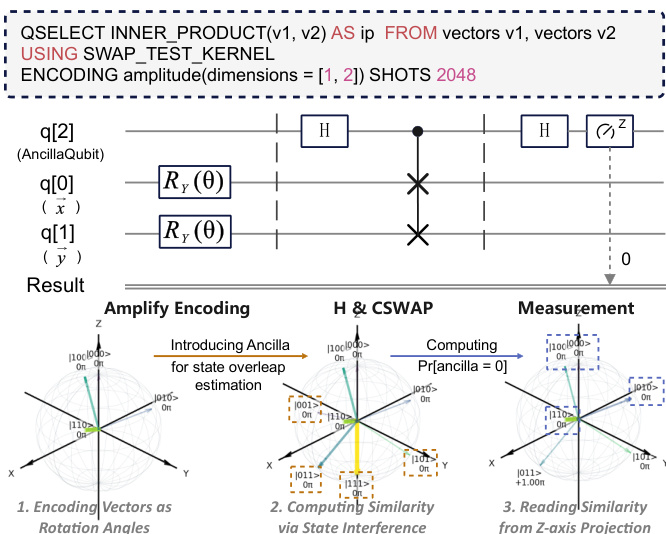
对于相似性连接，Qute 使用参数化 $R_Y(\theta)$RY​(θ) 旋转将向量编码为量子态，并通过 SWAP 测试估计其内积。如下图所示，辅助量子比特初始化为叠加态，条件地在两个数据寄存器间应用 CSWAP 门，最终的 Hadamard 门允许测量重叠概率。内积估计为 $|\langle x|y\rangle|^2 = 2 \cdot \text{Pr}[\text{ancilla} = 0] - 1$∣⟨x∣y⟩∣2=2⋅Pr[ancilla=0]−1，从而无需显式逐维遍历即可实现高效相似性检测。

聚合被重新表述为概率估计任务。准备所有行标识符的均匀叠加态，每行的值 $v(x)$v(x) 通过与 $v(x)/V_{\max}$v(x)/Vmax​ 成比例的旋转控制一个“Good”量子比特。测量 Good 量子比特为 $|1\rangle$∣1⟩ 的概率对应归一化平均值，全局总和通过振幅估计恢复：$\text{SUM}(v) = N \cdot V_{\max} \cdot \text{Pr}[\text{Good} = 1]$SUM(v)=N⋅Vmax​⋅Pr[Good=1]。

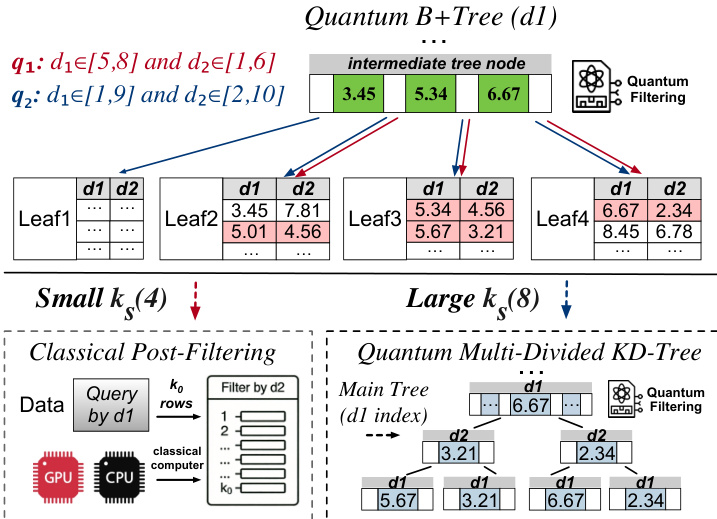
为缓解量子内存约束，Qute 采用量子感知索引。对于多维查询，首先在单个维度上探测轻量级量子 B⁺-树以识别候选集。如果候选集大小 $k_s$ks​ 较小（例如 $O(\log N)$O(logN)），则应用经典后过滤。如果 $k_s$ks​ 较大，系统升级为量子多分 KD 树，联合索引多个维度，使用量子辅助探测递归剪枝搜索空间。如下图所示，这种混合策略根据中间结果的基数动态选择经典或量子路径。

优化器将量子操作符建模为随机、精度有界的原语。时间估计 $T_q$Tq​ 考虑电路层中门持续时间和控制开销。成功概率 $P_q$Pq​ 由门错误率和退相干推导，近似为 $P_q = \prod_{k=1}^{K} p_k$Pq​=∏k=1K​pk​，其中 $p_k = (1 - \sum_{g \in L_k} \epsilon_g) \cdot \exp(-t_k / T_2^{\text{eff}})$pk​=(1−∑g∈Lk​​ϵg​)⋅exp(−tk​/T2eff​)。混合执行误差 $\varepsilon_q$εq​ 通过回退模型纳入：$\mathbb{E}[T_q] = P_q \cdot T_q^{\text{quantum}} + (1 - P_q) \cdot T_q^{\text{classical}}$E[Tq​]=Pq​⋅Tqquantum​+(1−Pq​)⋅Tqclassical​。运行时优化根据噪声调整，如增加采样次数、切换电路变体或回退到经典执行——均在有界误差语义下确保结果可信度。

实验

• 实现了一个最小 Qute 原型，将数据过滤卸载到 72 量子比特的噪声 QPU，使用 QPanda3 和 origin_wukong，每次实验 2000 次采样。
• 在包含 2^40 个元组的合成数据集上评估，使用选择性过滤查询，谓词选择性上限为 2%。
• 与使用基于成本模型方法的经典数据库进行比较，确保算法公平性。
• 测量和建模的 Qute 性能高度一致，验证了成本模型在大规模外推中的有效性。
• Qute 在小数据集上表现不如经典系统，但在超过约 2^30 个元组时超越经典系统，展示了极端规模无索引过滤的可扩展性。