一句话总结

来自 Skoltech 和 HSE 的作者表明，尽管重建性能很高，稀疏自编码器（SAE）仅能恢复 9% 的真实特征，并且随机基线变体在可解释性任务中表现与训练好的 SAE 相当，这挑战了 SAE 在分解神经网络机制方面的可靠性。

主要贡献

• 在合成设置中，尽管重建性能很高，SAE 仍无法恢复真实特征，表明解释方差并不意味着有意义的分解——即使解释方差达 71%，也仅恢复了 9% 的真实特征。
• 我们引入了三种简单基线，将编码器或解码器参数固定为随机值，从而直接评估所学习的特征方向或激活是否对 SAE 在真实模型激活上的表现有实际贡献。
• 在多个 SAE 架构和下游任务（包括可解释性、稀疏探测和因果编辑）中，这些基线与完全训练的 SAE 表现相当，表明当前 SAE 并未可靠地学习可解释的内部机制。

引言

作者利用稀疏自编码器（SAE）来解释大型语言模型，旨在将密集激活分解为人类可解释的特征——这是理解模型行为、安全性和对齐的关键目标。然而，先前工作缺乏真实标签来验证 SAE 是否恢复了有意义的结构，而近期研究显示，尽管重建得分较高，SAE 在下游任务中表现往往不佳。作者引入了三种简单基线——冻结解码器、冻结编码器和软冻结解码器——将学习参数固定或约束为随机值，发现这些基线在可解释性、探测和因果编辑任务中与完全训练的 SAE 表现相当。他们的合成实验进一步揭示，SAE 仅恢复高频特征，而非预期的分解，表明当前评估指标可能具有误导性，且 SAE 可能并未学习真正有意义的特征。

数据集

• 作者在 ℝ¹⁰⁰ 中生成合成激活，使用从单位球面上均匀采样的 3200 个真实特征向量组成的过完备字典。
• 每个激活向量是这些特征的稀疏线性组合，系数来自 Log-Normal(0, 0.25) 分布，二元激活指示符来自 Bernoulli(p_i)。
• 测试了两种激活概率设置：常数概率模型（p_i = 0.00625）和可变概率模型（p_i ~ Log-Uniform(10⁻⁵.⁵, 10⁻¹.²)），两者平均每个样本激活 20 个特征。
• 合成数据集用于训练两种 SAE 变体——BatchTopK 和 JumpReLU——字典大小为 3200，目标 L0 稀疏度为 20，与真实情况匹配。
• 重建保真度通过解释方差衡量，比较 SAE 输出与原始激活，归一化为均值预测的方差。
• 特征恢复通过计算每个真实特征与其最接近的 SAE 解码器向量之间的最大余弦相似度来评估。
• 尽管解释方差较高（0.67），但在常数概率设置下，两种 SAE 变体均未恢复有意义的真实特征，凸显了对齐挑战。

方法

作者利用稀疏自编码器（SAE）将神经网络激活分解为可解释的稀疏特征表示。该方法直接应对多义性——即单个神经元编码多个不相关概念的现象——基于叠加假设。该假设认为，神经网络通过将特征编码为激活空间中方向的稀疏线性组合，压缩超出其维度容量的特征。对于输入激活向量 $\mathbf{x} \in \mathbb{R}^{n}$x∈Rn，模型假设：

其中 $\mathbf{f}_j$fj​ 是真实潜在特征方向（$m \gg n$m≫n），$a_j$aj​ 是稀疏非负系数。SAE 通过学习特征向量字典 $\mathbf{d}_j$dj​ 和稀疏激活 $z_j$zj​ 来近似此分解：

其中 $\mathbf{W}^{\mathrm{dec}}$Wdec 是解码器矩阵，其列为学习到的特征方向。编码器通过 $\mathbf{z} = f(\mathbf{W}^{\text{enc}}\mathbf{x} + \mathbf{b}^{\text{enc}})$z=f(Wencx+benc) 映射输入，其中 $f$f 通常是诱导稀疏性的激活函数（如 ReLU），$\mathbf{b}^{\text{enc}}$benc 是学习的偏置。完整重建包括解码器偏置：$\hat{\mathbf{x}} = \mathbf{W}^{\text{dec}}\mathbf{z} + \mathbf{b}^{\text{dec}}$x^=Wdecz+bdec。为实现更丰富的表示，SAE 通常过完备，扩展因子 $k = m/n > 1$k=m/n>1，通常设为 16、32 或 64。

训练由复合目标引导，平衡重建保真度和稀疏性：

其中 $\lambda$λ 调整权衡。替代稀疏机制包括 L0 约束或自适应阈值，但核心原则不变：优化重建和稀疏性应产生与真实模型特征 $\mathbf{f}_j$fj​ 对齐且对应人类可解释概念的特征方向 $\mathbf{d}_j$dj​。

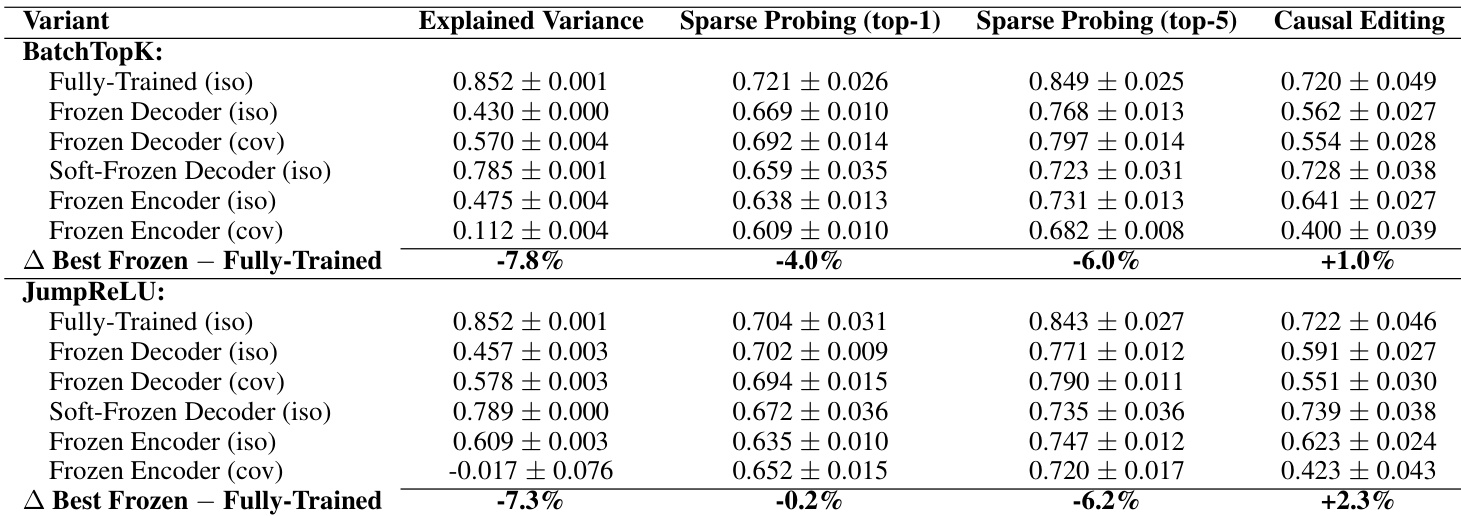
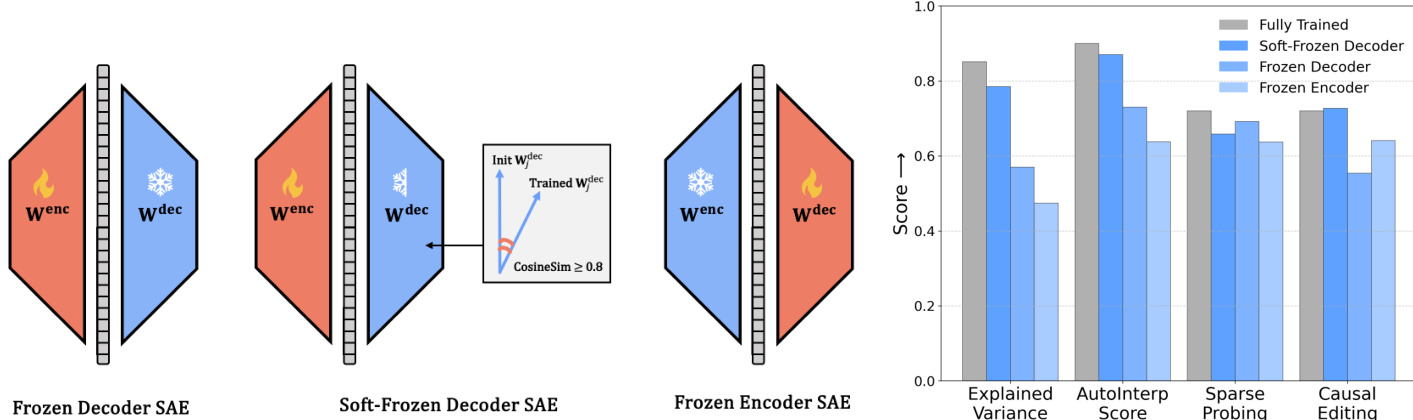
如下图所示，作者探索了三种训练模式：冻结解码器、软冻结解码器和冻结编码器 SAE。在冻结解码器变体中，解码器权重在初始化后固定，仅训练编码器。在软冻结解码器中，解码器用预训练权重初始化，仅当与初始权重的余弦相似度保持高于 0.8 时才更新。在冻结编码器中，编码器固定，仅训练解码器。这些配置在解释方差、AutoInterp 分数、稀疏探测和因果编辑等指标上进行评估，揭示了可解释性与重建性能之间的权衡。

实验

• 合成实验表明，SAE 仅恢复 9% 的真实特征，尽管解释方差达 71%，表明重建成功并不意味着特征发现。
• 在真实 LLM 激活上，具有冻结随机组件的 SAE 在可解释性、稀疏探测和因果编辑方面表现与完全训练的 SAE 相当，表明性能源于随机对齐而非学习的分解。
• 特征恢复偏向高频成分，而长尾的稀有特征大部分未被覆盖。
• 软冻结解码器基线表现几乎与训练好的 SAE 相当，支持“懒惰训练”模式，即对随机初始化的微小调整足以获得强指标。
• TopK SAE 在合成设置中成功，但在真实数据中失败，冻结变体仍表现相当，削弱了有意义特征学习的主张。
• 在视觉模型（CLIP）上的结果与语言模型一致，表明随机 SAE 无需训练即可产生类似可解释的特征。
• 总体而言，当前 SAE 并未可靠分解内部模型机制；标准指标可能反映统计伪影而非真实特征发现。

作者使用冻结随机基线测试稀疏自编码器（SAE）是否真正学习有意义的特征，或仅利用统计模式。结果表明，具有随机初始化和冻结组件的 SAE 在重建、可解释性、稀疏探测和因果编辑指标上表现几乎与完全训练的模型相当，表明当前 SAE 并未可靠分解模型内部机制。

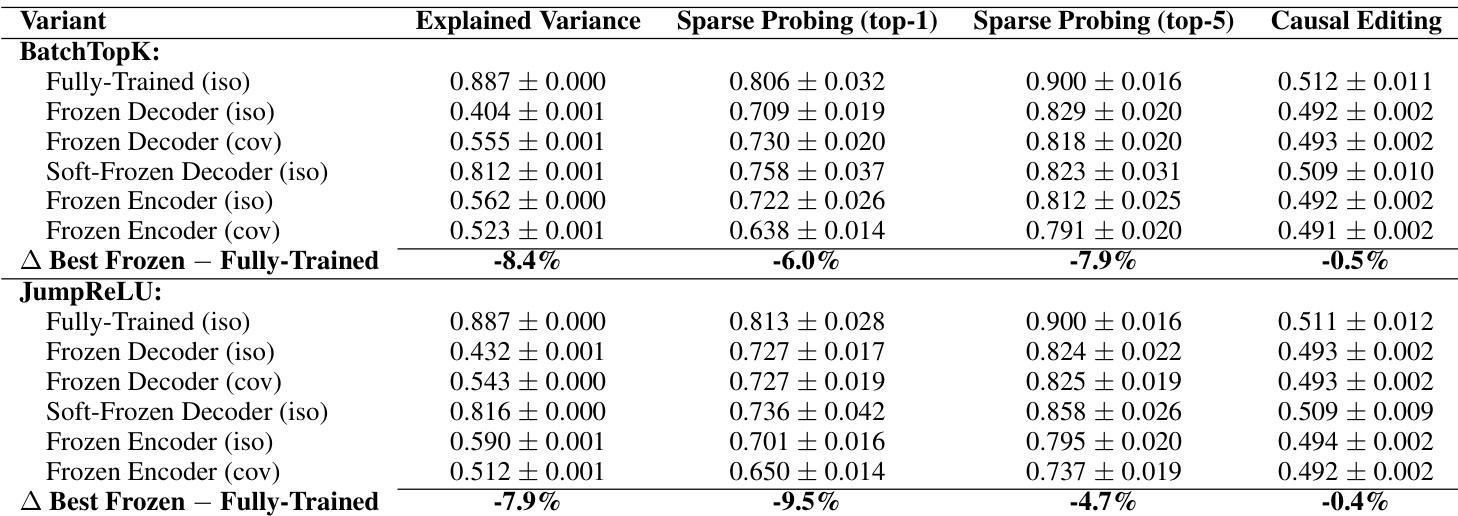
作者使用冻结随机基线测试稀疏自编码器（SAE）是否真正学习有意义的特征，或仅利用统计模式。结果表明，关键组件固定为随机值的 SAE 在重建、可解释性、稀疏探测和因果编辑任务中表现几乎与完全训练的模型相当，表明当前 SAE 并未可靠分解内部模型机制。

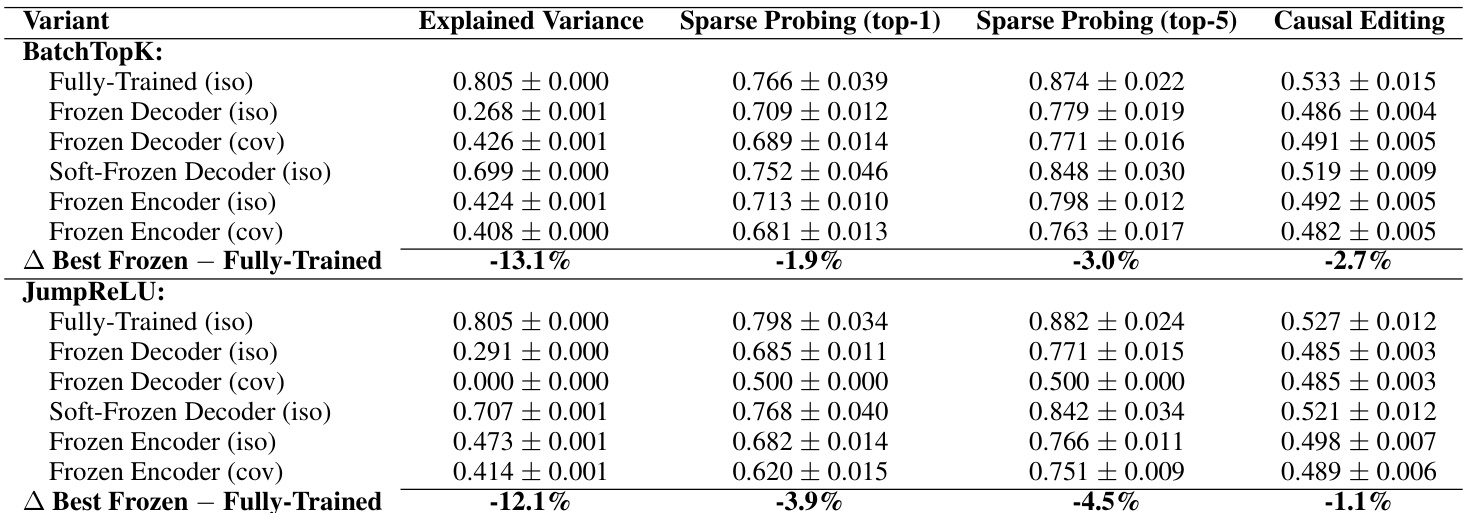
作者使用冻结随机基线测试稀疏自编码器（SAE）是否真正学习有意义的特征，或仅利用统计模式。结果表明，关键组件在随机初始化时固定的 SAE 在重建、可解释性、稀疏探测和因果编辑任务中表现几乎与完全训练的模型相当，表明当前 SAE 并未可靠分解内部模型机制。