一句话总结

来自港科大（广州）、新加坡国立大学及合作者的研究人员提出 ReAlign 和 ReVision，通过建模多模态学习中模态间隙的几何结构——稳定偏置与各向异性残差——来解决模态间隙问题，从而实现无需训练的高效对齐，并利用非配对数据替代昂贵的图文对，实现可扩展的多模态大语言模型（MLLM）预训练。

主要贡献

• 我们提出了“固定框架模态间隙理论”，将视觉与文本嵌入之间的几何错位分解为在冻结参考框架内的稳定偏置与各向异性残差，纠正了先前过度简化的各向同性假设。
• 我们提出了 ReAlign，一种无需训练的对齐方法，利用非配对数据的统计信息，通过锚点对齐、迹对齐和质心对齐三步将文本表示映射到图像嵌入空间，实现无需额外训练的精确几何校正。
• 我们提出了 ReVision，一种可扩展的 MLLM 预训练范式，利用 ReAlign 以非配对文本数据替代昂贵的图文对，在指令微调前使模型学习视觉分布，同时保持性能。

引言

作者利用多模态对比学习中已知的几何缺陷——模态间隙——重新思考多模态大语言模型（MLLM）的训练方式。先前方法假设该间隙是各向同性噪声，仅校正均值偏移，无法捕捉表征错位的真实各向异性结构，限制了可扩展性。作者的核心贡献是将间隙精确分解为稳定偏置与各向异性残差，从而实现 ReAlign：一种无需训练的三步统计对齐方法，仅使用非配对数据即可将文本嵌入映射到视觉分布。在此基础上，他们提出 ReVision，一种可扩展的两阶段训练范式：预训练阶段用海量文本替代昂贵图文对，随后用真实图像微调——证明当对齐正确时，文本本身即可编码丰富的视觉语义。

方法

作者利用固定参考框架，将模态间隙分解为可解释的几何分量，从而精确刻画双编码器对比模型中的持续错位。该分解基于数据驱动的子空间构建，分离偏置项与残差项，允许独立估计，并将理论断言简化为可从有限样本估计的二阶矩条件。

该框架首先在大规模图文数据集上使用 InfoNCE 损失训练双编码器模型。在固定参考时刻 $t_0$t0​，从保留的探测集构建任务相关子空间 $U$U，通过计算两种模态单位归一化嵌入的经验协方差：

$$\hat{\Sigma}(t_0) := \mathrm{Cov}_{\mathbf{p}}\big(e_x(t_0)\big) + \mathrm{Cov}_{\mathbf{p}}\big(e_y(t_0)\big),$$Σ^(t0​):=Covp​(ex​(t0​))+Covp​(ey​(t0​)),

其中 $U := \mathrm{span}\{q_1, \ldots, q_r\}$U:=span{q1​,…,qr​} 由 $\hat{\Sigma}(t_0)$Σ^(t0​) 的前 $r$r 个特征向量导出（由能量阈值确定）。然后定义正交补空间 $V := U^\perp$V:=U⊥，并为后续所有分析保持固定的正交投影算子 $P_U$PU​ 和 $P_V$PV​。此固定框架允许将模态间隙 $\Delta(t) := e_x(t) - e_y(t)$Δ(t):=ex​(t)−ey​(t) 分解为偏置与残差分量。

偏置项定义为投影均值分量：$\beta(t) := P_U \mathbb{E}[\Delta(t)] \in U$β(t):=PU​E[Δ(t)]∈U（主模态偏置，PMB）和 $\gamma(t) := P_V \mathbb{E}[\Delta(t)] \in V$γ(t):=PV​E[Δ(t)]∈V（常数正交偏置，COB）。零均值残差为 $\delta(t) := P_U(\Delta(t) - \mathbb{E}[\Delta(t)]) \in U$δ(t):=PU​(Δ(t)−E[Δ(t)])∈U 和 $\zeta(t) := P_V(\Delta(t) - \mathbb{E}[\Delta(t)]) \in V$ζ(t):=PV​(Δ(t)−E[Δ(t)])∈V。由此得到精确的正交分解：

$$\Delta(t) = \beta(t) + \delta(t) + \gamma(t) + \zeta(t).$$Δ(t)=β(t)+δ(t)+γ(t)+ζ(t).

如下图所示，残差结构在两个子空间中均表现出极端各向异性，正交分量 $V$V 中包含一个稳定的偏置向量，其几何上与 $\zeta(t)$ζ(t) 的高度拉伸噪声结构解耦。

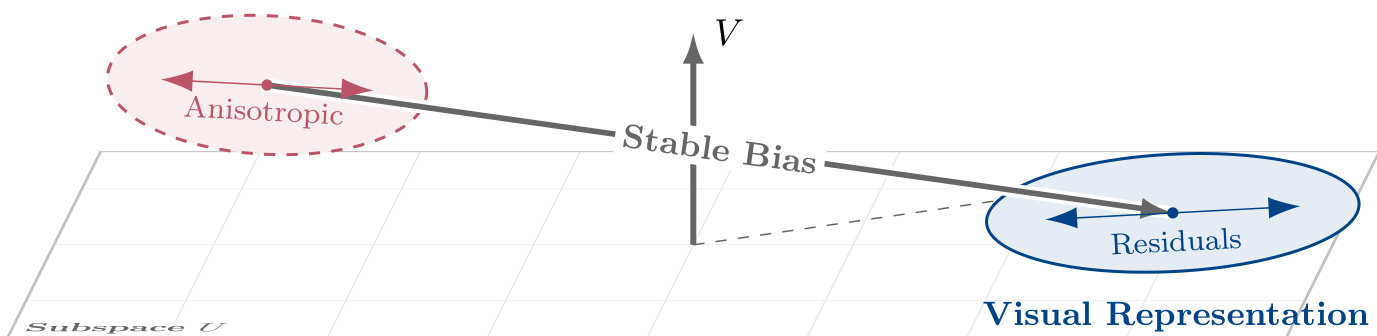
作者进一步分析这些分量的演化。经验上观察到梯度集中在瞬时任务子空间 $U_t$Ut​ 内，参考泄漏比 $\|P_V g_t\| / \|g_t\|$∥PV​gt​∥/∥gt​∥ 紧密跟踪几何基线 $\sin\theta(U_t, U)$sinθ(Ut​,U)。这种集中意味着在 $V$V 中的直接优化可忽略，导致 $\gamma(t)$γ(t) 被动漂移——由子空间旋转而非主动梯度校正驱动的缓慢累积演化。相比之下，在 $U$U 内，残差 $\delta(t)$δ(t) 表现出极端各向异性（$\kappa(\Sigma_U) > 10^3$κ(ΣU​)>103），并迅速与梯度协方差结构对齐，表明波动与任务语义耦合。

为在不重新训练的情况下解决这些几何错位，作者提出 ReAlign，一种三阶段、无需训练的对齐策略。该方法在球面投影前于欧几里得空间操作，包括：

1. 锚点对齐：将源模态居中并平移其均值以匹配目标模态质心：$\dot{e}_y = (e_y - \mu_y) + \mu_x$e˙y​=(ey​−μy​)+μx​。
2. 迹对齐：通过 $s = \sqrt{\mathcal{T}_x / \mathcal{T}_y}$s=Tx​/Ty​​ 缩放残差以匹配目标全局能量，得到 $\tilde{e}_y = \mu_x + s(e_y - \mu_y)$e~y​=μx​+s(ey​−μy​)，保留源模态的各向异性结构。
3. 质心对齐：通过显式重新居中分布校正球面投影引起的非线性漂移：$e_y'' = e_y' - \mu' + \mu_x$ey′′​=ey′​−μ′+μx​，随后重新归一化。

如 ReAlign 流程图所示，该序列确保最终对齐表示在单位超球面上匹配目标模态的一阶与二阶统计量，同时保留语义层级并减轻伪漂移。

这一基于几何的方法构成了 ReVision 的基础——一种用于多模态大语言模型的可扩展两阶段训练范式。第一阶段，ReAlign 用于从非配对文本合成伪视觉嵌入，从而在海量文本语料上进行预训练。第二阶段，模型在真实图文指令对上微调以精炼细粒度视觉推理。推理时，模型直接接收真实图像，受益于预训练阶段建立的非对称对齐。

实验

• ReAlign 通过建模各向异性协方差有效减少模态间隙，优于因几何瓶颈受限的各向同性方法（如 C³）。
• ReVision 通过保留语义层级与角度拓扑，在多模态大语言模型训练中实现更优性能，提升推理能力并减少幻觉。
• 使用 ReAlign 扩展非配对文本数据（200万样本）在成本降低26%的情况下超越100万真实图文对的性能，证明成本效益扩展可行。
• ReAlign 在约1万样本下快速收敛，Float64精度稳定，时间复杂度线性，内存占用恒定，支持可扩展部署。
• 领域特定统计至关重要；跨领域对齐会降低性能，凸显定制校准的必要性。
• 分块协方差对齐因数值不稳定与语义失真而失败，而 ReAlign 的各向同性缩放保留局部结构并确保鲁棒性。
• 短描述优于长描述，因其协方差更紧凑、秩更低且信噪比更高，揭示语言密度可能损害几何对齐。
• 定性分析证实 ReVision 在抽象推理、空间理解、细粒度感知及跨认知任务的知识整合方面表现优异。

ReVision 在所有评估类别（包括通用感知、复杂推理与抗幻觉）中均优于 BC Align，取得更高平均分。结果证实 ReVision 的几何对齐策略比分块协方差方法更好地保留语义结构，后者因数值不稳定与语义失真而表现不佳。这使得在无需配对图文数据的情况下实现更鲁棒、更准确的多模态理解成为可能。

结果表明，使用各向异性几何对齐的 ReVision 在通用感知、推理与幻觉基准上持续优于其长描述变体。性能差距凸显：简洁、几何紧凑的描述比语言丰富但噪声大的长描述能实现更稳定的模态对齐。这表明，对于有效的跨模态训练，信噪比与流形结构比原始文本长度更重要。

作者使用 ReVision 通过建模各向异性协方差对齐文本与图像模态，相比 C³ 等各向同性方法显著减少几何间隙。结果表明，ReVision 在通用感知、推理与幻觉基准上优于基线，证明精确几何对齐能保留语义结构并提升下游任务性能。使用 ReVision 扩展纯文本预训练在性能上也超越配对图文训练，同时降低数据获取成本。

ReVision-2M 在通用、推理与幻觉基准上取得最高平均分，优于纯文本与配对图文基线，同时降低26%数据获取成本。该方法的几何对齐策略比基于各向同性噪声的方法更好地保留语义结构，即使在无真实图像输入时也能实现优越性能。使用精确对齐扩展非配对文本数据被证明比依赖昂贵配对数据集更具成本效益和竞争力。