一句话总结

来自包括 $^{*12}$∗12 和 $^{*1}$∗1 在内的机构的研究人员提出了一种受 Focal Loss 启发的难度感知优势缩放系数，用于 RLVR，以缓解对常见轨迹的偏好。该方法集成到 GRPO、DAPO 和 CISPO 中，在不增加计算成本的情况下提升了 Qwen2.5-7B 的 pass@256，增强了跨领域的鲁棒性。

主要贡献

• 我们识别并量化了组相对 RLVR 中的一种关键采样偏差：由于计算限制，中等组大小最可能导致在更新过程中遗漏稀有正确轨迹，从而引发分布锐化，即使总正确质量在增长。
• 我们推导出了一个闭式尾部遗漏概率，表明其随组大小呈现非单调行为，并揭示了即使整体正确性提高，未采样正确质量仍可能缩小，从而解释了先前关于最优 rollout 数量研究中的矛盾发现。
• 我们提出了 F-GRPO，一种受 Focal Loss 启发的难度感知优势缩放方法，通过降低高成功率提示的权重以保留多样性；该方法在不增加组大小或计算成本的情况下，提升了 Qwen2.5-7B 在 GRPO、DAPO 和 CISPO 上的 pass@256。

引言

作者利用可验证奖励的强化学习（RLVR）对大型语言模型进行推理任务微调，通过自动可检查奖励避免昂贵的人类反馈。虽然 RLVR 提高了 top-1 准确率，但常导致输出分布锐化，降低解的多样性，损害高采样预算下的性能——这种权衡限制了其在复杂或开放性问题中的有效性。先前工作在组相对策略优化（GRPO）中对组大小的指导存在冲突，尚无明确共识如何平衡探索与效率。作者的主要贡献是 F-GRPO，一种轻量级的、难度感知的优势缩放方法，可在不增加 rollout 数量的情况下缓解分布锐化。它针对锐化最严重的中等组大小，恢复高-k 性能（如 pass@256），同时保持 pass@1，且使用比大组少 4 倍的 rollout。

数据集

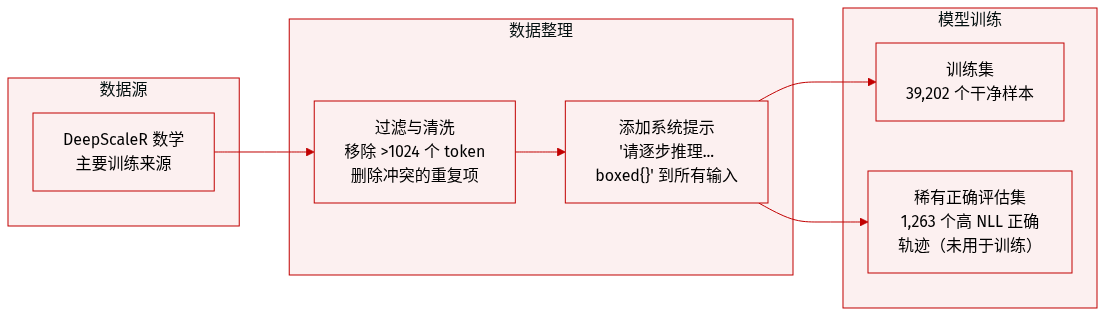
• 作者使用 DeepScaleR 数学数据集（Luo 等，2025）作为主要训练来源，过滤掉长度超过 1024 个 token 的样本，并移除答案冲突的重复样本，最终得到 39,202 个干净训练样本。
• 他们在每个训练输入前添加固定系统提示：“请逐步推理，并将最终答案放入 \boxed{} 中。”以标准化推理格式。
• 为评估稀有正确行为，他们从训练集中采样 256 个提示，并使用基础模型为每个提示生成 800 个 rollout，仅保留正确轨迹。
• 从这些轨迹中，他们计算基础模型下的长度归一化 NLL，并选择 NLL 最高的前 1% 正确轨迹作为“稀有正确”子集——总计 1,263 条轨迹——用于衡量训练模型对初始低概率正确解的赋值能力。
• 此稀有正确子集不用于训练，仅用于评估：训练模型下更高的 NLL 表明模型更不可能生成这些低概率正确解。

方法

作者利用一种难度感知的优势缩放机制，缓解可验证奖励强化学习（RLVR）中固有的集中偏差。该偏差源于有限组采样导致策略更新过度强化已可能的正确轨迹，而忽略稀有正确模式——即使总正确质量在增长。所提出的方法 F-GRPO（及其变体 F-DAPO 和 F-CISPO）引入了一种轻量级、按提示缩放的系数，灵感来自 Focal Loss，通过降低高成功率提示的更新权重，从而在不增加计算成本或组大小的情况下保留解空间的多样性。

该方法的核心观察是，组相对优势——如 GRPO、DAPO 和 CISPO 等算法中所用——在批奖励基线 $S_R > 0$SR​>0 时会诱导向已采样正确轨迹漂移。这是因为未采样动作（包括稀有正确动作）获得零奖励，但仍因优势计算中的基线减法而被惩罚。作者在分类策略框架中形式化了这一点，其中未采样动作 $i \in U$i∈U 的一步 logit 更新为：

$$\Delta z_i = -\frac{\eta}{N} S_R p_i$$Δzi​=−Nη​SR​pi​

当 $S_R > 0$SR​>0 时，该更新会驱动未采样正确质量下降，而这一条件与高经验成功率强相关。为在轨迹层面实现这一洞察，他们将提示 $x$x 的经验成功率定义为：

$$\widehat{\mu}_{\mathrm{pos}}(x) = \frac{\bar{R}(x) - R_w}{R_c - R_w} = \frac{X}{N}$$μ​pos​(x)=Rc​−Rw​Rˉ(x)−Rw​​=NX​

其中 $X$X 是组内正确 rollout 的数量。该统计量作为 $S_R$SR​ 驱动漂移幅度的代理：更高的 $\widehat{\mu}_{\mathrm{pos}}(x)$μ​pos​(x) 表示对已采样正确轨迹更强的集中压力。

为抵消这一效应，作者引入了一个难度权重：

$$g(x) = \left(1 - \widehat{\mu}_{\mathrm{pos}}(x)\right)^\gamma, \quad \gamma \geq 0$$g(x)=(1−μ​pos​(x))γ,γ≥0

该权重对同一提示的所有 rollout 统一缩放组相对优势。当 $\gamma = 0$γ=0 时，$g(x) = 1$g(x)=1，方法退化为标准 GRPO。当 $\gamma > 0$γ>0 时，高经验成功率的提示获得更小的梯度贡献，从而有效将优化压力转移到更困难的提示上，这些提示中稀有正确模式更可能被低估。

缩放后的优势定义为：

$$\widehat{A}_i^{\mathrm{F-GRPO}} := g(x) \cdot \widehat{A}_i^{\mathrm{GRPO}}$$AiF−GRPO​:=g(x)⋅AiGRPO​

该修改与算法无关，可直接集成到任何组相对 RLVR 方法中。它无需额外网络或参数，仅需标量超参数 $\gamma$γ，因此计算开销极低。作者证明，这一简单调整在多个基线方法（GRPO、DAPO、CISPO）上均提升了 pass@256，同时保持或改善了 pass@1，验证了该方法在不牺牲常见情况准确性的同时增强了解的多样性。

如下图所示，缩放后的优势大小 $g(x) \cdot |\widehat{A}^{\mathrm{GRPO}}|$g(x)⋅∣AGRPO∣ 随成功概率 $\mu_{\mathrm{pos}}(x)$μpos​(x) 增加而减小，尤其对正确 rollout 更明显。这直观展示了 F-GRPO 如何抑制高成功率提示的更新，将梯度贡献重新分配到更困难的案例上，这些案例中稀有正确轨迹更易被遗漏。

实验

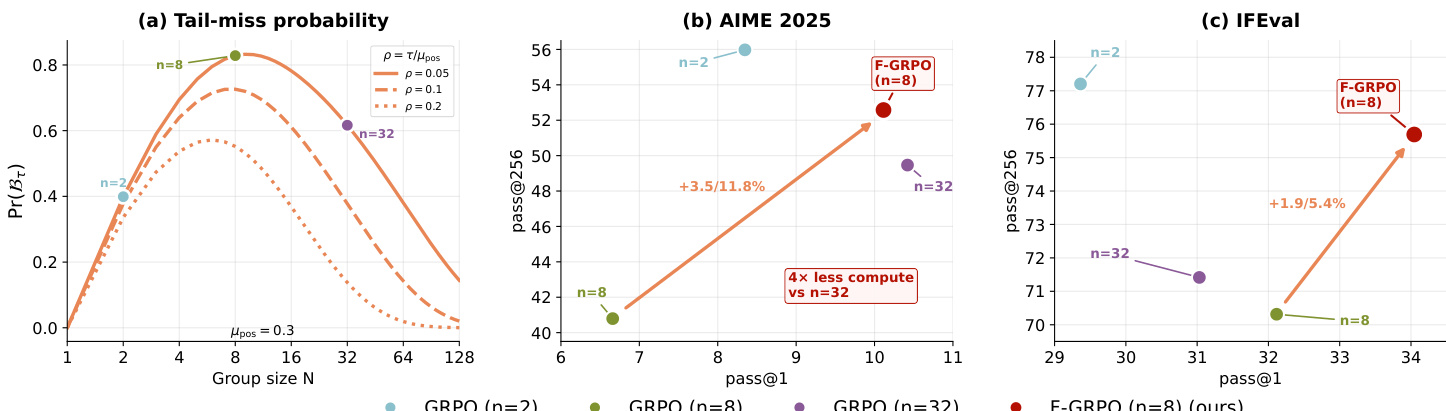
• RL 训练中的组大小 N 呈现三种模式：小 N 通过稀疏更新保留多样性，中等 N 导致分布锐化并出现尾部遗漏概率峰值，大 N 通过更好覆盖稀有正确模式恢复多样性。
• Focal 权重通过抑制高成功率提示的更新缓解中等 N 模式下的集中现象，在不牺牲 pass@1 的前提下提升 pass@256，并增强跨领域泛化能力。
• 经验 LLM 结果确认了理论三模式：N=2 偏向多样性，N=8 导致分布锐化，N=32 恢复多样性；在 N=8 下使用 Focal 权重的性能匹配或超过 N=32，且 rollout 更少。
• Focal 权重在多种方法（GRPO、DAPO、CISPO）和模型规模上持续提升 pass@256，常提升跨领域 pass@1，表明多样性保留有助于泛化。
• Focal 权重在 pass@1 和跨领域迁移上优于熵和 KL 正则化，提供了一种更简单、更有效的维持解多样性的替代方案。

作者使用 Focal 权重修改组相对策略优化方法，发现它在多个模型和基准测试中持续提升解多样性（pass@256），同时保持或略微提升单次尝试准确率（pass@1）。结果表明，Focal 权重缓解了概率质量集中在常见解上的现象，尤其在标准方法易导致分布锐化的中等组大小下。该方法在平衡准确性和多样性方面优于熵和 KL 正则化，尤其在跨领域任务上。

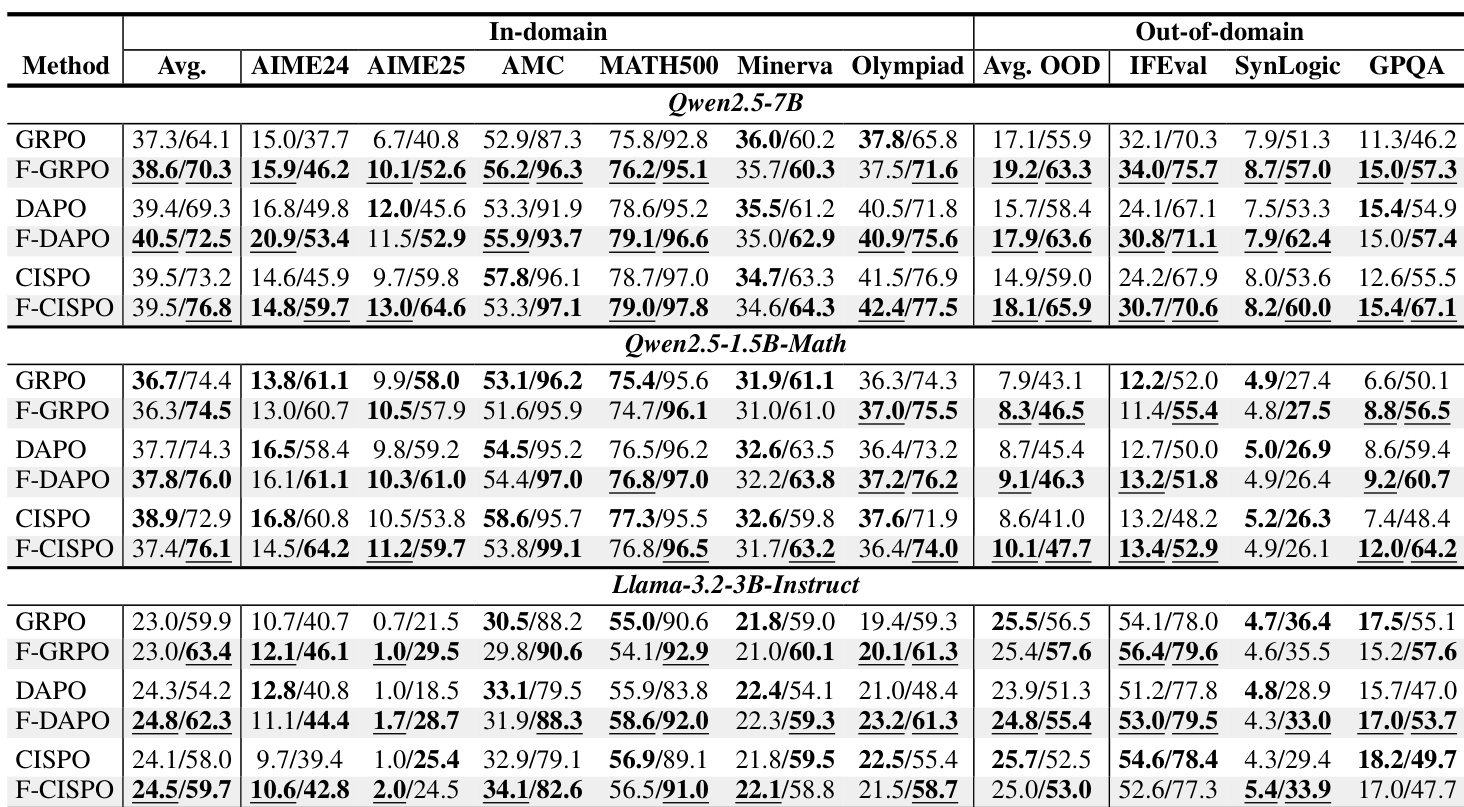
作者使用 Focal 权重调整训练期间的梯度贡献，基于跨模型和方法的性能选择 $\gamma$γ 值在 0.5 至 1.0 之间。结果表明，Focal 权重持续提升解多样性（pass@256），同时保持或略微提升单次尝试准确率（pass@1），尤其在常用组大小如 N=8 下。该方法缓解了概率质量集中在部分解上的现象，在无需额外 rollout 预算或复杂正则化的情况下保留稀有正确模式。

结果表明，F-GRPO 在保持或提升 pass@1 的同时，持续提升跨领域 pass@256，优于标准 GRPO 和 KL 正则化变体。该方法在不增加 rollout 成本的情况下实现这一点，表明 Focal 权重有效缓解了策略对常见解的集中。该模式在多个基准测试中成立，表明保留解多样性具有更广泛的泛化益处。

结果表明，GRPO 训练中的组大小显著影响解多样性和准确性，中等大小如 N=8 由于集中在常见解上，常导致 pass@1 与 pass@256 间的最尖锐权衡。在 N=8 下使用 Focal 权重通过保留稀有正确轨迹缓解了这一问题，实现与更大组相当的多样性，同时保持或提升单次尝试准确性。该方法还减少了与基础模型稀有解的偏差，体现在更低的 ΔNLLrare 值上。

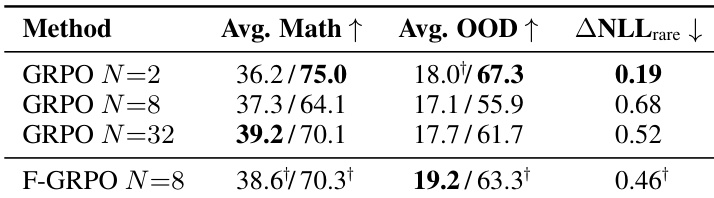
结果表明，GRPO 训练中的组大小在单次尝试准确率与解多样性之间形成权衡，中等大小如 N=8 常以牺牲多样性为代价锐化策略，而更小或更大的大小则保留更广泛的解覆盖范围。在 N=8 下使用 Focal 权重缓解了这种锐化，提升多样性指标而不牺牲准确性，并以更少的 rollout 匹配或超过更大组大小的性能。该效果在领域内和跨领域基准测试中均成立，表明 Focal 权重有助于保留稀有正确解，同时保持或提升整体性能。