一句话总结

来自中国人民大学、阿里巴巴、厦门大学和大连大学的研究人员提出了 MathForge——一个结合 DGPO 和 MQR 的双框架，通过难度感知的策略更新和多维度问题重构，优先处理更难的问题，从而增强大语言模型的数学推理能力，在多个基准测试中优于先前方法。

主要贡献

• 我们识别并修正了组相对策略优化（GRPO）中的关键不平衡问题，提出难度感知组策略优化（DGPO），通过平均绝对偏差归一化优势估计，并更重地加权更难的问题，使训练聚焦于可解决的弱点。
• 我们引入多维度问题重构（MQR），这是一种数据增强策略，通过在多个维度（如添加故事背景或嵌套子问题）上系统性地重构问题以增加难度，同时保留原始正确答案以确保可验证性。
• MathForge 结合 DGPO 和 MQR，在多个数学推理基准测试中实现了最先进的性能，显著优于现有 RLVR 方法，并通过在多种模型上的广泛实验验证了其有效性。

引言

作者利用可验证奖励的强化学习（RLVR）来提升大语言模型的数学推理能力，该方法通过基于规则的评分避免了昂贵的神经奖励模型。然而，现有方法如组相对策略优化（GRPO）由于优势估计的不平衡，无意中抑制了对更难问题的更新；而数据增强方法则侧重于多样性，未系统性地增加难度。为解决此问题，他们提出 MathForge——一个结合难度感知组策略优化（DGPO，重新平衡更新幅度并更重地加权更难问题）和多维度问题重构（MQR，通过重构问题在故事、术语和子问题维度上增加难度，同时保留原始正确答案）的双框架。该方法构建了一个协同循环：更难、重构后的数据训练出能更好针对其弱点的模型，从而在多个基准测试中取得最先进的结果。

数据集

• 作者使用从公开 MATH 数据集派生的 MQR 增强数据，通过重构现有问题以增强数学推理任务。
• 数据不包含任何个人身份信息或敏感信息，确保符合隐私规范并符合 ICLR 伦理准则。
• 该数据集支持训练专注于提升 AI 数学能力的模型，潜在应用于科学、工程和教育领域。
• 本节未描述除问题重构外的裁剪、元数据构建或其他额外处理。

方法

作者利用改进的策略优化框架来增强语言模型的数学推理能力，基于组相对策略优化（GRPO）并引入两个核心组件：难度感知组策略优化（DGPO）和多维度问题重构（MQR）。整体训练过程在批处理设置中进行，从数据集 $\mathcal{D}$D 中采样查询，并使用旧策略 $\pi_{\theta_{\text{old}}}$πθold​​ 生成多个响应 $\{o_{si}\}${osi​}。每个响应被分配一个标量奖励 $r_{si}$rsi​（通常基于正确性），形成每个查询的奖励分布。然后，策略模型 $\pi_{\theta}$πθ​ 使用结合了每个响应组内相对优势的词元级目标进行更新。

[[IMG:|Framework diagram]]

该方法的核心 DGPO 解决了 GRPO 优化目标中的基本不平衡问题。GRPO 使用组相对优势估计（GRAE），其中响应 $o_i$oi​ 的优势 $\hat{A}_{\text{GR},i}$A^GR,i​ 通过将其奖励 $r_i$ri​ 与组平均奖励的差值归一化并除以标准差计算。这种归一化导致单个问题的总更新幅度依赖于准确率 $p$p，在 $p=0.5$p=0.5 时达到峰值，而在更简单或更难的问题上衰减。这种不平衡是有问题的，因为即使准确率非零的挑战性问题对有针对性的学习和模型改进至关重要。为解决此问题，DGPO 引入难度平衡组优势估计（DGAE），将分母中的标准差替换为奖励的平均绝对偏差（MAD）。这一改变确保任何问题的总更新幅度为常量值 $G$G，与准确率无关，从而平衡所有问题的影响，无论其难度如何。

此外，DGPO 采用难度感知问题级加权（DQW）明确优先处理更具挑战性的问题。这通过为批次中的每个查询 $q_s$qs​ 分配权重 $\lambda_s$λs​ 实现，该权重通过其响应平均奖励的负值的 softmax 计算，并由温度超参数 $T$T 缩放。平均奖励较低（即更难的问题）的查询获得更高权重，增加其对整体损失的贡献。最终的 DGPO 目标结合这些元素，使用 DGAE 优势 $\hat{A}_{\text{DG},si}$A^DG,si​ 和 DQW 权重 $\lambda_s$λs​ 在裁剪策略梯度损失中，同时对有效查询的有效词元平均损失以确保训练稳定性。

作为算法改进的补充，MQR 策略提供了以数据为中心的增强。它利用大型推理模型自动重构现有问题，生成保留原始答案的更复杂变体。这通过三种方法实现：添加故事背景引入噪声、发明抽象数学术语测试概念理解、将关键数值条件转换为独立子问题以强制多步推理。由此生成的增强数据集（结合原始和重构问题）为策略模型提供了更丰富、更具挑战性的训练环境，构建了一个协同循环：改进的数据支持更好的学习，而更好的学习使模型能够处理更复杂的重构问题。

实验

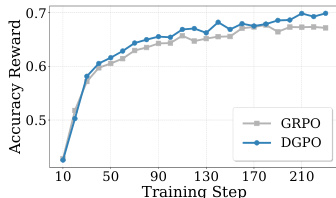
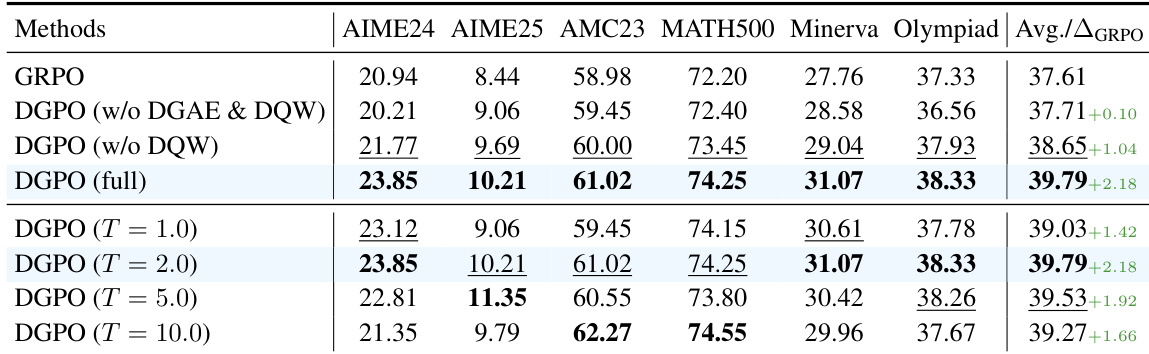
• 仅 DGPO 将 Qwen2.5-Math-7B 的 MATH 平均得分提升至 39.79%（对比 GRPO 的 37.61%），验证了通过 DGAE 和 DQW 实现的难度感知策略优化。
• MQR 通过添加叙事、抽象和嵌套逻辑重构增强数据，将性能提升至 41.04%，证明数据多样性增强了推理鲁棒性。
• MathForge（DGPO + MQR）在 MATH 上达到 42.17%，展示了协同效应：MQR 提供具有挑战性的数据，DGPO 优先学习弱点。
• MathForge 在不同模型（Qwen2.5-Math-1.5B、3B、DeepSeek-Math-7B）上均表现优异，持续超越基线，证实其模型无关的有效性。
• 在多模态领域，Qwen2.5-VL-3B-Instruct 上的 DGPO 在 GEOQA-8k 上达到 59.95%（对比 GRPO 的 57.43%），证明其跨域适用性。
• 消融实验显示 DGPO 组件贡献累积：DGAE（+0.94%）、DQW（+1.14%）；MQR 的三种策略协同作用，优于单个策略或 MetaMath-Rephrasing 基线。
• MQR 重构的问题更难（子问题准确率 72.04% 对比原始问题 79.77%），但在此类问题上训练能带来更好的泛化能力（“训练更难，测试更好”）。
• 即使较小的重构器（Qwen2.5-7B、Qwen3-30B）也能带来提升，表明 MQR 对重构器能力依赖较低。
• DGPO 可与 GPG、DAPO、GSPO 结合，进一步提升性能（如 DAPO+DGPO：39.91%），证实其作为通用增强模块的兼容性。

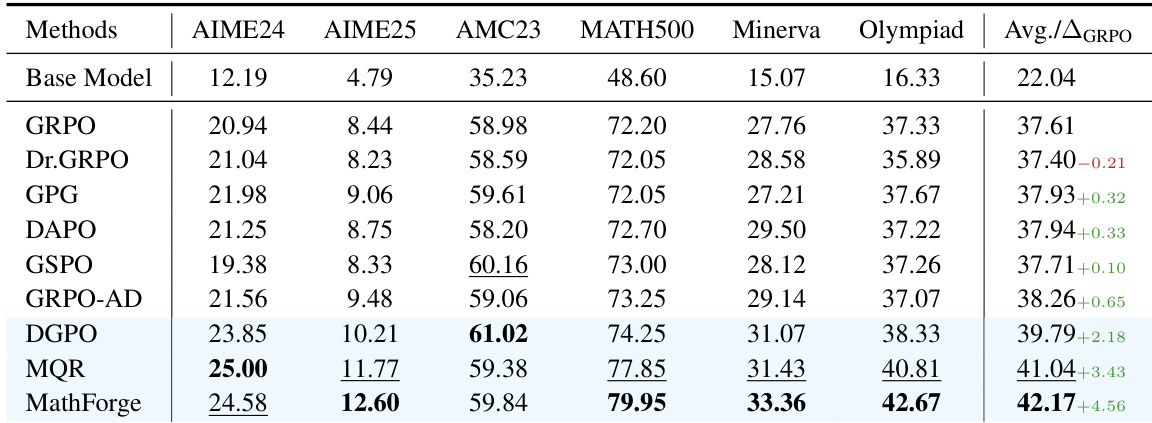
作者使用 Qwen2.5-Math-7B 模型评估其 MathForge 框架（结合 DGPO 和 MQR）的有效性。结果表明，MathForge 在所有基准测试中均取得最高平均性能，优于各个组件及 GRPO 基线，比 GRPO 提升 4.45%。

作者使用 Qwen2.5-VL-3B-Instruct 模型在多模态领域的 GEOQA-8k 数据集上评估 DGPO 算法。结果表明，DGPO 取得最高性能 59.95%，显著优于 GRPO 基线的 57.43%。

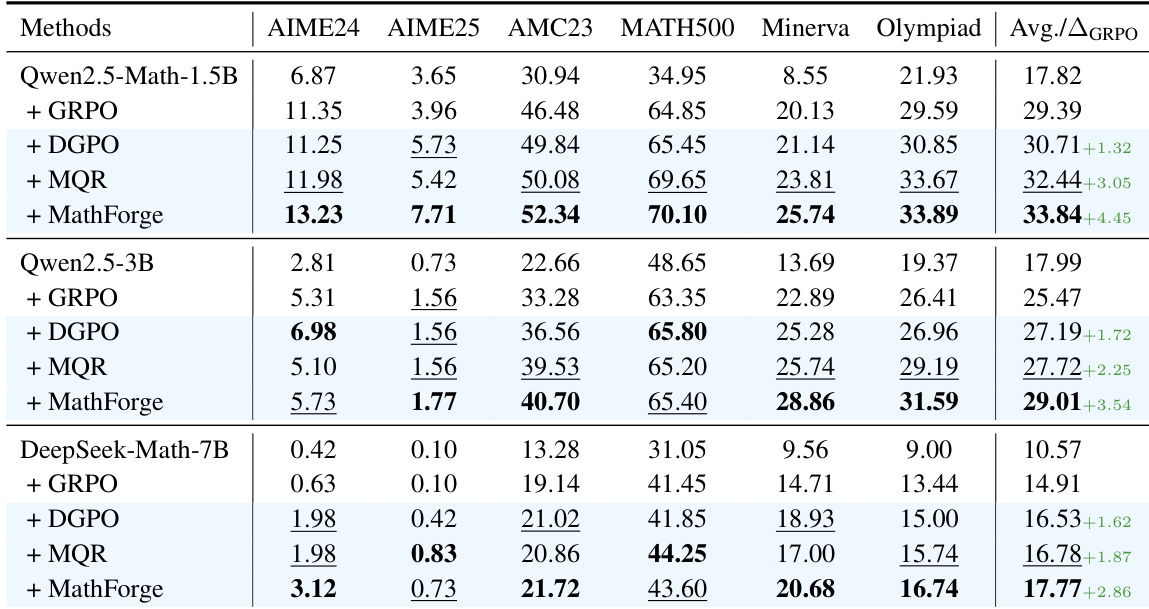
作者使用 Qwen2.5-Math-7B 模型在 MATH 数据集上评估各种强化学习方法，结果表明 MathForge 在所有基准测试中取得最高平均性能。结果表明，MathForge 优于所有单个组件和基线，平均得分为 42.17%，显著优于 GRPO 基线的 37.61%。

作者使用不同温度设置的 DGPO 分析问题难度加权对模型性能的影响。结果表明，温度设置为 2.0 时取得最高平均分 39.79%，优于更低和更高的温度设置，表明该值在优先处理挑战性问题的同时保持对整个批次的学习，实现了最优平衡。

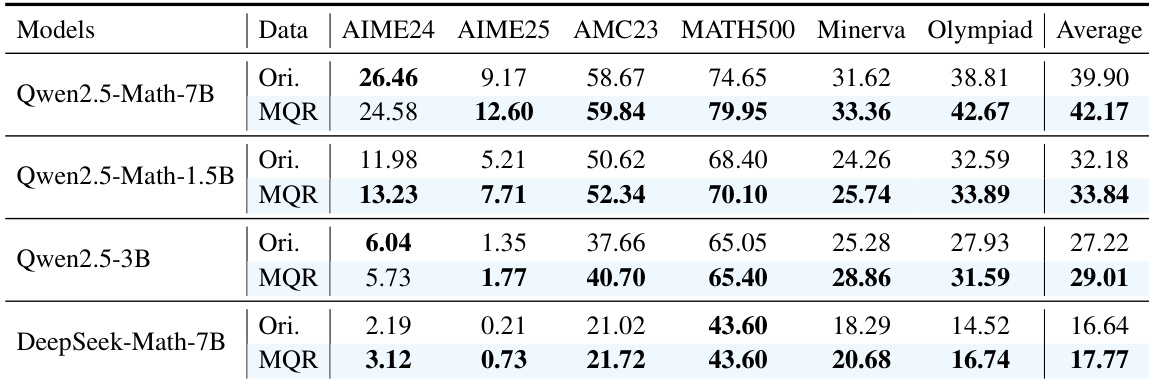
作者使用 Qwen2.5-Math-7B 模型在 MATH 数据集上评估 MathForge 的有效性，比较原始数据与 MQR 增强数据在多个基准测试中的性能。结果表明，MQR 在所有基准测试中持续优于原始数据，Qwen2.5-Math-7B 模型在 MQR 增强数据上平均得分为 42.17%，显著高于原始数据的 39.90%。