一句话总结

华中科技大学与通义实验室的研究人员提出 DenseGRPO 框架，通过引入密集的步级奖励来对齐文本到图像生成中的人类偏好，利用自适应随机性校准探索过程，克服稀疏奖励问题，显著提升流匹配模型的性能。

主要贡献

• DenseGRPO 通过基于 ODE 的方法评估中间干净图像，为 GRPO 基础的文本到图像模型引入步级密集奖励，解决稀疏奖励问题，使反馈与每一步去噪贡献对齐。
• 该方法揭示并修正了均匀探索与随时间变化的噪声强度之间的不匹配，提出一种奖励感知的 SDE 采样器，按时间步自适应调整随机性，确保去噪轨迹上的探索均衡。
• 在多个基准测试上的实验确认 DenseGRPO 的最先进性能，验证了密集奖励对流匹配模型中有效对齐人类偏好的必要性。

引言

作者利用流匹配模型进行文本到图像生成，并通过强化学习解决其与人类偏好对齐的持续挑战。先前基于 GRPO 的方法因采用单一终端奖励应用于所有去噪步骤而面临稀疏奖励问题，导致反馈与各步骤实际贡献脱节，阻碍细粒度优化。DenseGRPO 通过基于 ODE 的中间图像评估估计步级奖励增益，引入密集奖励，确保反馈与各步骤贡献匹配。此外，通过按时间步自适应调整 SDE 采样器中的随机性校准探索，修正奖励分布的不平衡。实验确认 DenseGRPO 的最先进性能，验证了密集、步感知奖励对有效对齐的必要性。

数据集

• 作者仅使用公开可用的数据集，所有数据集均符合其各自许可证，确保符合 ICLR 伦理准则。
• 本研究未涉及人类受试者、敏感个人数据或专有内容。
• 所介绍的方法无预见性滥用或危害风险。
• 提供的文本中未描述数据集构成、子集细节、训练划分、混合比例、裁剪策略或元数据构建。

方法

作者将流匹配模型中的去噪过程重新表述为马尔可夫决策过程（MDP），以实现基于强化学习的对齐。在此表述中，时间步 $t$t 的状态定义为 $\mathbf{s}_t \triangleq (\pmb{c}, t, \pmb{x}_t)$st​≜(c,t,xt​)，其中 $\pmb{c}$c 为提示词，$t$t 为当前时间步，$\pmb{x}_t$xt​ 为潜在表示。动作对应预测的先验潜在变量 $\pmb{x}_{t-1}$xt−1​，策略 $\pi(\mathbf{a}_t \mid \mathbf{s}_t)$π(at​∣st​) 建模为条件分布 $p(\pmb{x}_{t-1} \mid \pmb{x}_t, \pmb{c})$p(xt−1​∣xt​,c)。奖励是稀疏且轨迹级的，仅在终端状态 $t=0$t=0 分配为 $\mathcal{R}(\pmb{x}_0, \pmb{c})$R(x0​,c)，中间步骤奖励为零。此设计导致不匹配：相同的终端奖励用于优化所有时间步，忽略了各个去噪步骤的独特贡献。

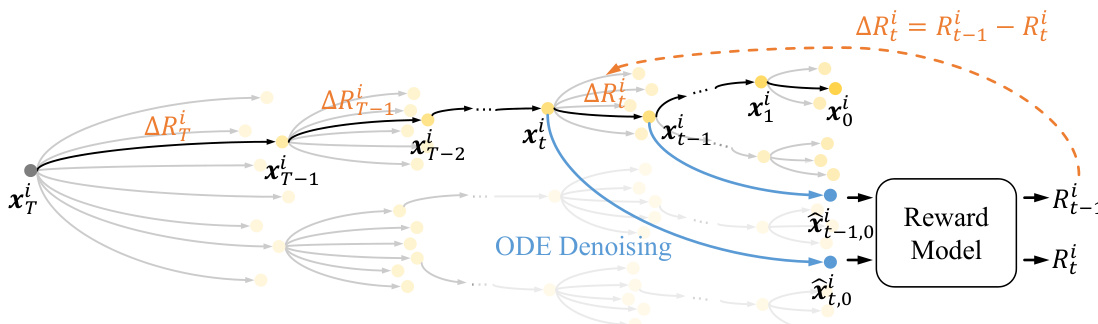
为解决此问题，DenseGRPO 引入步级密集奖励机制。该方法不依赖单一终端奖励，而是为轨迹中每个中间潜在变量 $\pmb{x}_t^i$xti​ 估计奖励 $R_t^i$Rti​。这通过利用 ODE 去噪过程的确定性实现：给定 $\pmb{x}_t^i$xti​，模型可通过 $n$n 步 ODE 去噪确定性生成对应的干净潜在变量 $\hat{\pmb{x}}_{t,0}^i$x^t,0i​，即 $\hat{\pmb{x}}_{t,0}^i = \mathrm{ODE}_n(\pmb{x}_t^i, \pmb{c})$x^t,0i​=ODEn​(xti​,c)。$\pmb{x}_t^i$xti​ 的奖励被分配为 $R_t^i \triangleq \mathcal{R}(\hat{\pmb{x}}_{t,0}^i, \pmb{c})$Rti​≜R(x^t,0i​,c)，其中 $\mathcal{R}$R 为预训练奖励模型。步级密集奖励 $\Delta R_t^i$ΔRti​ 定义为连续步骤间的奖励增益：$\Delta R_t^i = R_{t-1}^i - R_t^i$ΔRti​=Rt−1i​−Rti​。此公式提供细粒度、步级特定的反馈信号，反映每个去噪动作的实际贡献。

参见框架图，展示密集奖励估计过程。图中显示，对于每个潜在变量 $\pmb{x}_t^i$xti​，计算 ODE 去噪轨迹以获得干净对应物 $\hat{\pmb{x}}_{t,0}^i$x^t,0i​，然后由奖励模型评估以产生 $R_t^i$Rti​。密集奖励 $\Delta R_t^i$ΔRti​ 由连续潜在奖励的差值导出，实现每步信用分配。

在 GRPO 训练循环中，密集奖励 $\Delta R_t^i$ΔRti​ 替代稀疏终端奖励用于优势计算。第 $i$i 条轨迹在时间步 $t$t 的优势重新计算为：

这确保每个时间步的策略更新由反映该步骤即时贡献的奖励信号引导，而非全局轨迹结果。

为进一步增强训练期间的探索，DenseGRPO 引入奖励感知的 SDE 采样器噪声注入校准。虽然现有方法在所有时间步使用统一噪声水平 $a$a，DenseGRPO 按时间步调整噪声强度 $\psi(t)$ψ(t) 以维持均衡的探索空间。校准迭代进行：对每个时间步 $t$t，算法采样轨迹，计算密集奖励 $\Delta R_t^i$ΔRti​，并根据正负奖励的平衡调整 $\psi(t)$ψ(t)。若正负奖励数量大致相等，则增加 $\psi(t)$ψ(t) 以鼓励多样性；否则减少以恢复平衡。校准后的噪声调度 $\psi(t)$ψ(t) 随后用于 SDE 采样器，将原始 $\sigma_t = a\sqrt{t/(1-t)}$σt​=at/(1−t)​ 替换为 $\sigma_t = \psi(t)$σt​=ψ(t)，从而根据去噪过程的时间变化特性定制随机性。

实验

• DenseGRPO 在组合图像生成、人类偏好对齐和视觉文本渲染任务中优于 Flow-GRPO 和 Flow-GRPO+CoCA，通过步级密集奖励展示出与目标偏好的更优对齐。
• 消融研究确认，步级密集奖励显著优于稀疏轨迹奖励，时间特定噪声校准增强了探索有效性。
• 增加 ODE 去噪步骤可提高奖励准确性和模型性能，尽管计算成本更高，验证了精确奖励估计对对齐的关键作用。
• DenseGRPO 可推广至扩散模型和更高分辨率，通过确定性采样保持性能增益，实现准确潜在奖励预测。
• 尽管实现强对齐，DenseGRPO 在特定任务中略有奖励作弊倾向，表明奖励精度与鲁棒性之间存在权衡，可通过更高质量奖励模型缓解。

作者使用 DenseGRPO 在文本到图像生成中引入步级密集奖励，在组合、文本渲染和人类偏好任务中一致优于 Flow-GRPO 和 Flow-GRPO+CoCA。结果表明，密集奖励信号更好地将反馈与各去噪步骤对齐，提升语义准确性和视觉质量，而消融研究确认校准探索和多步 ODE 去噪对奖励准确性的关键作用。尽管在特定指标下出现部分奖励作弊，DenseGRPO 在不同模型架构和分辨率下表现出鲁棒性和通用性。