一句话总结

MIT 与 Meta FAIR 的研究人员提出了 SOAR，这是一种元强化学习框架，使大语言模型能够通过将教师奖励锚定在学生进步上（而非内在信号），为无法解决的问题生成自构建的课程，从而在无需人工筛选数据的情况下突破推理瓶颈。

主要贡献

• SOAR 引入了一种双层元强化学习框架，使预训练的大语言模型能够为最初无法解决的难题生成合成课程，其奖励机制基于可测量的学生进步，而非内在代理指标。
• 在初始成功率接近零（0/128）的数学基准测试中，SOAR 通过将教师奖励锚定于真实性能提升（而非自洽性或解题质量），可靠地避免了先前自对弈方法中常见的不稳定性和崩溃。
• 分析表明，生成问题的结构质量和良构性比答案正确性更能驱动学习，证明即使在无先验解题能力的情况下，也能自然产生有用的学习阶梯。

引言

作者针对大语言模型在推理任务微调中的核心局限展开研究：当初始成功率接近零时，基于可验证奖励的强化学习（RLVR）因信号稀疏而失效。以往的自对弈和课程方法依赖内在或代理奖励（如自洽性或梯度范数），这些奖励在符号领域（正确性为二值）中常退化为无意义或不可学习的任务。作者提出 SOAR——一种元强化学习框架，其中教师模型为学生模型生成合成问题，仅当学生在少量真实难题上表现提升时才给予奖励。这种基于真实表现的双层方法避免了奖励作弊，并能在模型初始无法解决目标问题时实现学习，揭示了通过自生成阶梯可挖掘潜在知识，无需人工干预。

数据集

• 作者使用三个数学推理基准数据集——MATH、HARP 和 OlympiadBench——研究无自动验证场景下的稀疏二值奖励。这些数据集涵盖 AMC、AIME、USA(J)MO 和国际奥赛题目。

• 对每个数据集，应用“fail@128”过滤：使用 Llama-3.2-3B-Instruct（1024 token 预算，temperature 1.0）对每题采样 128 个解，仅保留成功率 0/128 的题目。由此创建极具挑战的子集，直接训练收效甚微。

• OlympiadBench：仅使用 674 道英文、纯文本、可自动验证的题目。因原始数据集仅为测试集，随机划分为 50-50 的训练/测试集。

• HARP：使用完整数据集，同样随机划分为 50-50 的训练/测试集。

• MATH：为避免记忆偏差（Llama-3.2-3B-Instruct 在 MATH 官方训练集上准确率更高），初始题目池从 5000 题的官方测试集抽取。经 fail@128 过滤后，自建 50-50 训练/测试划分。所有训练与评估仅使用该内部划分。

• 数据集规模：最终训练/测试划分见表 2。测试集规模更大（占过滤后数据的 50%），以可靠衡量性能提升，克服随机波动。

• 除过滤与划分外，未提及裁剪或元数据构建。所有合成数据与师生训练仅使用内部训练划分；最终结果仅在保留测试划分上评估。

方法

作者利用教师-学生元强化学习框架 SOAR，使预训练语言模型能自动生成解决难题所需的学习阶梯。该框架为非对称自对弈系统：两个模型由同一基础模型初始化，在嵌套循环中训练。教师模型 $\pi_{\phi}^{T}$πϕT​ 生成合成问答对 $(q, a)_{\text{synthetic}}$(q,a)synthetic​，用于训练学生模型 $\pi_{\theta}^{S}$πθS​。学生在内循环中通过强化学习学习回答教师生成的问题；其在目标数据集中一组真实难题上的表现，作为外循环中教师的奖励信号。此反馈机制使教师被激励生成能提升学生解决难题能力的合成问题，而教师本身无需直接观察这些难题。

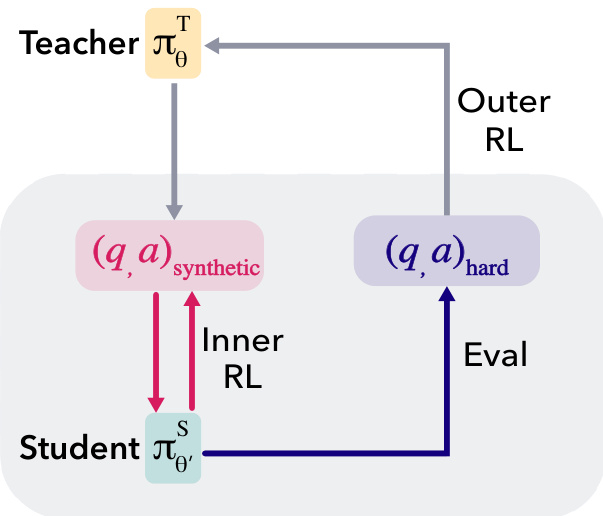
框架核心为双层优化问题：目标是生成合成数据集 $\mathcal{X}$X，使其用于训练学生时最大化学生在目标领域上的表现。为实现计算可行性，作者将该目标实例化为嵌套元强化学习循环：外循环使用 RLOO（带环外优化的强化学习）训练教师生成合成问答对；内循环使用标准 RLVR（基于价值的强化学习奖励）在教师生成的数据集上训练学生。关键创新在于教师奖励信号锚定于学生在难题上的真实表现，而非使用内在奖励。该黑盒奖励信号确保教师因生成退化或无用问题而受罚，仅当合成课程带来真实学习进展时才获奖励。

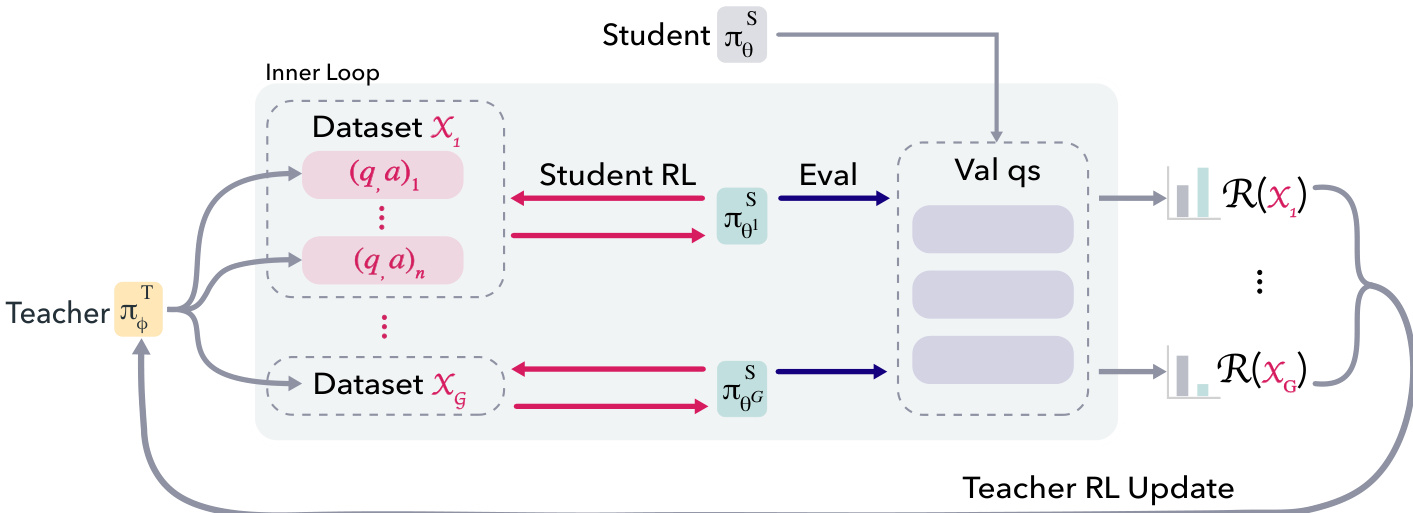
在外循环中，教师生成 $g \cdot n$g⋅n 个合成问答对，划分为 $g$g 个大小为 $n$n 的数据集。对每个数据集 $\mathcal{X}_k$Xk​，执行内循环：在 $\mathcal{X}_k$Xk​ 上训练学生固定步数（10），然后在原始训练集的子采样难题集 $\mathcal{Q}_R$QR​ 上评估学生策略。数据集 $\mathcal{X}_k$Xk​ 的奖励为学生在 $\mathcal{Q}_R$QR​ 上成功率相对于基线学生的平均提升。为降低噪声，该奖励在 $r$r 个并行学生训练中取平均。教师随后基于这些数据集级奖励使用 RLOO 算法更新。

内循环涉及在合成数据集 $\mathcal{X}_k$Xk​ 上使用 RLOO 训练学生。学生仅训练少量步数，以诱导可测量的策略变动同时控制计算成本。每次内循环后，学生恢复为基线策略进入下一轮。为应对教师适应进步学生的问题，引入晋升机制：跟踪教师奖励的移动平均，当其超过固定阈值 $\tau$τ 时，将学生基线重置为前轮表现最佳的学生策略。该累积数据集（促成学生晋升）被存储为“晋升问题”（PQ）用于评估。

实验

• SOAR 在 MATH 和 HARP 上训练师生对（OlympiadBench 保留作 OOD 测试），使用 Llama-3.2-3B-Instruct，外循环 200 步，每轮 n=64 样本；若 3 步移动平均奖励超过 τ=0.01，则晋升学生。
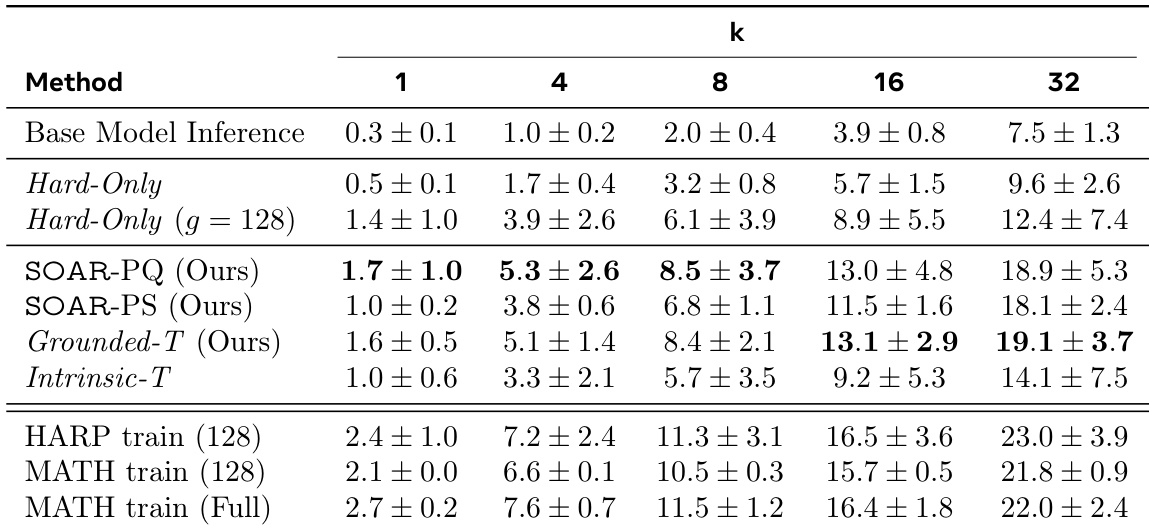
• 晋升学生（PS）在 MATH 上 pass@32 提升 +8.5%，在 HARP 上 +3.6%（对比 Hard-Only）；晋升问题（PQ）在 MATH 上提升 +9.3%，在 HARP 上 +4.2%，证实合成问题（而非训练轨迹）驱动性能提升。
• PQ 在 OlympiadBench 上迁移有效（MATH-PQ +6%，HARP-PQ +3% 对比 Hard-Only），显示跨数据集泛化能力，且未进行 OOD 优化。
• PQ 恢复了完整 MATH 训练（6750 题）75% 的性能增益，HARP 的 50%；HARP-PQ 优于 128 道真实 HARP 题，与 128 道真实 MATH 题表现相当。
• Grounded-T 教师优于 Intrinsic-T 和 Base-T，学生轨迹更稳定且多样性更高（Vendi Score 34.91 vs. Intrinsic-T 的 10.82）；Intrinsic-T 在 1/3 种子中出现高方差与崩溃。
• 合成问题无需正确——仅 32.8% 的 PQ 问题完全正确——但结构连贯性与多样性更重要；元强化学习比 Base-T 更少产生歧义错误。
• Hard-Only 使用 4 倍计算资源（组大小 128）在 MATH 上仅提升 +2.8% pass@32，远低于 PQ 增益。
• 教师策略本身通过元强化学习提升：Grounded-T 问题匹配 PQ 性能并稳定学生学习曲线；晋升机制至关重要。
• 多轮问题生成表现不如单轮；Grounded-T 采样更大数据集（128 vs. 64）可降低方差而不牺牲均值性能。
• 教师训练遵循探索-利用循环；基于真实表现的奖励在收敛时保持多样性，而内在奖励则导致多样性崩溃。

作者使用 SOAR 生成提升学生在难题集上表现的合成问题，结果表明 SOAR-PQ 和 SOAR-PS 方法在所有 pass@k 指标上显著优于 Hard-Only 和 Intrinsic-T 基线。表现最佳的方法 SOAR-PQ（MATH）和 SOAR-PS（HARP）分别达到 12.0 ± 3.0 和 11.7 ± 1.6 的 pass@32 分数，证明基于真实表现的元强化学习有效发现有用课程，突破性能瓶颈。

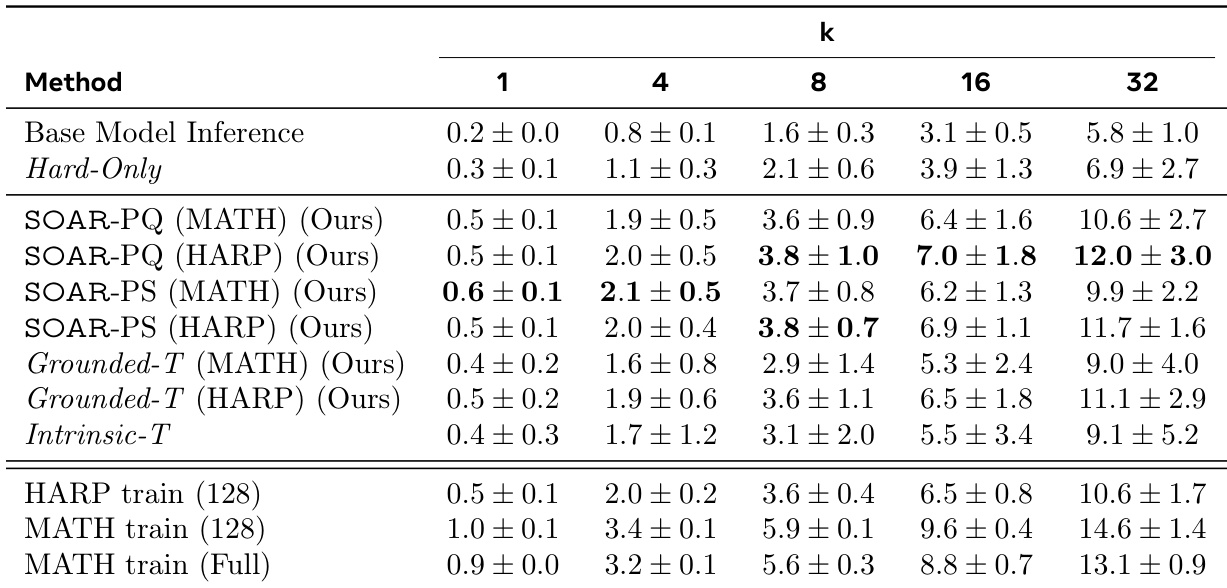
作者使用 SOAR 生成提升学生在难题集上表现的合成问题，结果表明 SOAR-PQ 和 SOAR-PS 在所有 pass@k 指标上显著优于 Hard-Only 和 Intrinsic-T 基线。表现最佳的方法 SOAR-PQ 达到 19.1% 的 pass@32 准确率，部分情况下甚至超越完整 MATH 训练集，同时在 OlympiadBench 上展现强跨数据集泛化能力。

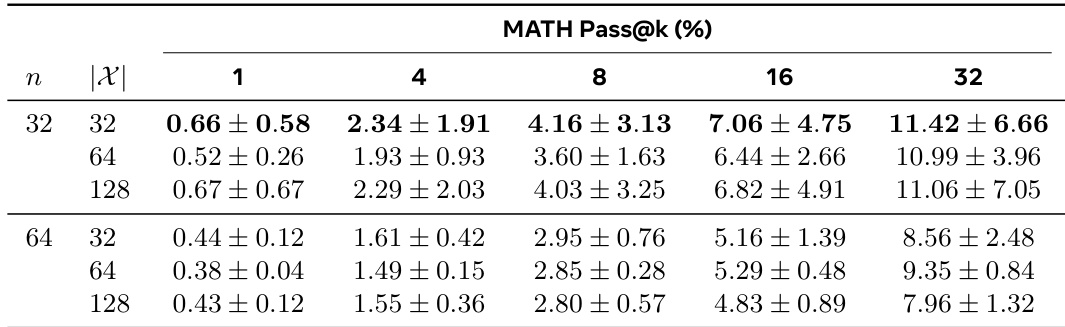
作者使用表格展示数据集大小与样本数量对 MATH 数据集中学生表现的影响。结果表明，样本数量从 32 增加到 64 可提升所有 pass@k 指标表现，而数据集大小从 32 增加到 128 道题通常导致表现下降，尤其在较高 k 值时更明显。

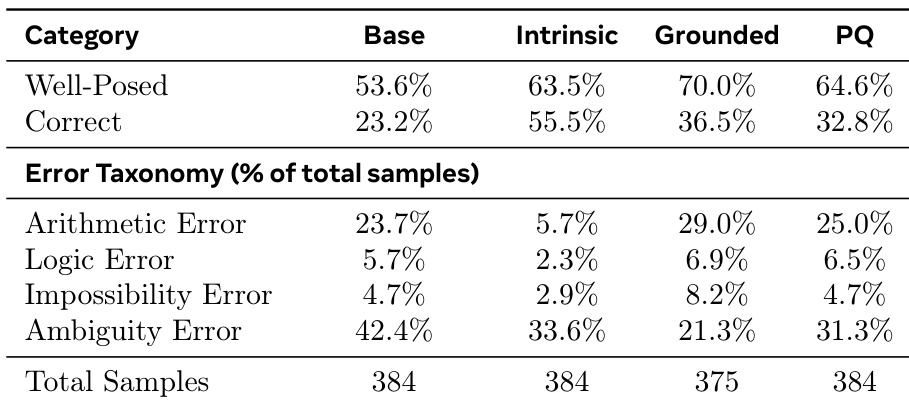
作者使用表格比较不同教师模型生成的合成问题的正确性与错误类型。结果表明，基于真实表现的奖励生成的问题在良构性与正确率上优于内在与基础模型，而内在奖励虽产生最高正确率，但歧义与逻辑错误显著更高。数据表明，问题结构与连贯性比答案正确性对提升学生表现更重要。

作者使用元强化学习框架训练教师模型，生成合成问题以提升学生在难题集上的表现。结果表明，教师生成的问题显著优于基线，表现最佳的方法在 MATH 和 HARP 上的 pass@k 准确率高于直接在真实数据上训练。