一句话总结

北京大学与腾讯混元的研究人员提出了 iFSQ，这是一种改进的标量量化方法，通过分布匹配解决激活坍塌问题，从而实现公平的 AR-扩散模型基准测试；他们揭示 4 位/维度为最优配置，并表明扩散模型在天花板性能上优于自回归模型，该洞见进一步扩展至 LlamaGen-REPA。

主要贡献

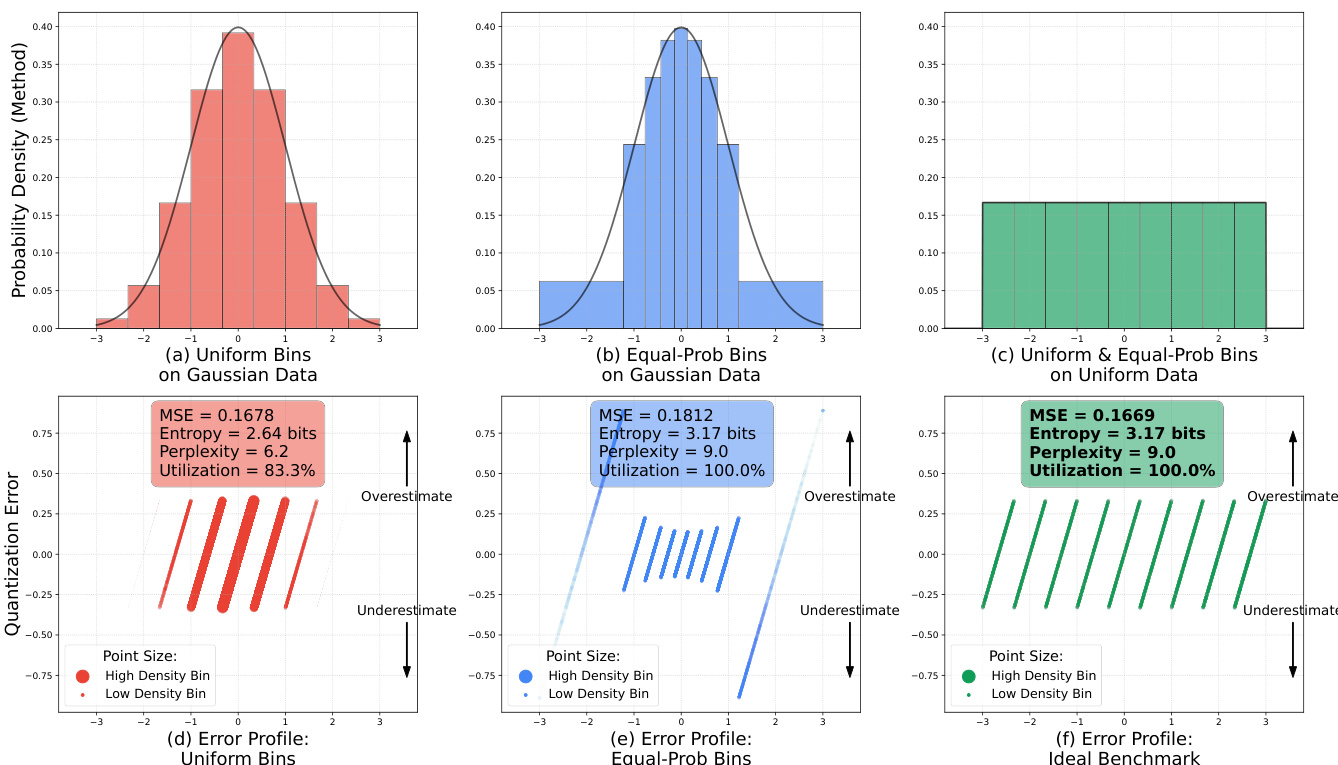
• 我们引入 iFSQ，这是对有限标量量化（FSQ）的一行代码增强，将 tanh 激活替换为分布匹配函数，确保均匀的桶利用率和最优重建保真度，通过将高斯隐变量映射到均匀先验实现。
• 使用 iFSQ 作为统一的分词器，我们建立了一个受控基准，揭示出每维度 4 位在离散与连续表示之间取得最佳平衡，且扩散模型尽管收敛较慢，但最终质量优于自回归模型。
• 我们将表示对齐（REPA）方法适配至自回归图像生成，创建了具有更强正则化（λ=2.0）的 LlamaGen-REPA，证明性能提升，同时确认跨生成范式特征对齐的益处。

引言

作者利用有限标量量化（FSQ）统一自回归与扩散图像生成，使用单一分词器解决长期存在的 VQ-VAE 和 VAE 造成的碎片化问题。原始 FSQ 因等间隔量化与神经激活的类高斯分布不匹配而导致激活坍塌，迫使在重建保真度与桶利用率之间做出权衡。其主要贡献是 iFSQ —— 通过将 tanh 替换为分布匹配激活的一行代码修改 —— 在保持等间隔的同时强制均匀先验，同时实现最优保真度与效率。这使得公平基准测试成为可能，揭示每维度 4 位为最佳点，且扩散模型尽管收敛较慢，但在峰值质量上优于 AR 模型。他们进一步通过将表示对齐适配至 AR 模型，创建了 LlamaGen-REPA。

方法

作者采用基于量化的视觉分词框架，弥合生成模型中连续与离散表示范式之间的鸿沟。该方法的核心建立在有限标量量化（FSQ）之上，它允许在无需显式可学习码本的情况下进行离散分词。这种设计支持高效且稳定的分词，适用于自回归和基于扩散的生成任务。分词器架构包括一个编码器，将输入图像 $x \in \mathbb{R}^{H \times W \times 3}$x∈RH×W×3 压缩为低分辨率隐表示 $z \in \mathbb{R}^{h \times w \times d}$z∈Rh×w×d，通常通过 8× 或 16× 下采样实现。解码器随后从隐空间重建图像，形成完整的压缩-解压缩流程。

对于扩散模型，量化隐变量 $z_{\text{quant}}$zquant​ 直接作为扩散过程的输入。量化首先应用边界函数 $f: \mathbb{R} \to [-1, 1]$f:R→[−1,1]（通常为双曲正切函数）约束隐值。量化分辨率由每通道 $L = 2^K + 1$L=2K+1 个层级定义，其中 $K$K 决定量化层级数。连续隐变量 $z$z 通过逐元素四舍五入映射为离散整数索引 $q \in \{0, \ldots, L-1\}^d$q∈{0,…,L−1}d，如公式定义：

$$q_j = \mathrm{round} \left( \frac{L - 1}{2} \cdot (f(z_j) + 1) \right)$$qj​=round(2L−1​⋅(f(zj​)+1))

此操作将范围 $[-1, 1]$[−1,1] 映射到整数集 $\{0, \ldots, L-1\}${0,…,L−1}。量化索引随后通过以下方式映射回连续空间，用于扩散模型：

$$z_{\mathrm{quant}, j} = \left( q_j - \frac{L - 1}{2} \right) \cdot \frac{2}{L - 1}$$zquant,j​=(qj​−2L−1​)⋅L−12​

此步骤引入有损压缩，其中 $z_{\mathrm{quant}} \approx z$zquant​≈z，在保持连续隐空间结构特性的同时实现离散分词。

对于自回归模型，量化索引 $q$q 通过双射的基-$L$L 展开转换为单一标量令牌索引 $I$I：

$$I = \sum_{j=1}^{d} q_j \cdot L^{d-j}$$I=j=1∑d​qj​⋅Ld−j

此转换确保从 $d$d 维量化向量到标量索引的唯一映射，使自回归模型能够按序预测令牌。隐式码本大小为 $|\mathcal{C}| = L^d$∣C∣=Ld，随维度 $d$d 指数增长，但避免了 VQ-VAE 中可学习码本的内存和稳定性问题。

作者通过将 tanh 激活替换为缩放的 sigmoid 函数，对标准 FSQ 流程进行修改，以实现更均匀的量化值分布。具体而言，边界函数替换如下：

$$z = 2 \cdot \mathrm{sigmoid}(1.6 \cdot z) - 1$$z=2⋅sigmoid(1.6⋅z)−1

此修改改善了变换分布的均匀性，对保持量化表示质量至关重要。量化过程进一步使用直通估计器处理训练期间的梯度流。四舍五入后的隐变量 $z_{\text{rounded}}$zrounded​ 计算如下：

$$z_{\text{rounded}} = \mathrm{round}(z_{\text{scaled}})$$zrounded​=round(zscaled​)

其中 $z_{\text{scaled}} = z \cdot \text{halfWidth}$zscaled​=z⋅halfWidth，且 $\text{halfWidth} = (L - 1)/2$halfWidth=(L−1)/2。随后应用估计器：

$$z_{\hat{}} = z_{\text{rounded}} - z_{\text{scaled}}.\text{detach} + z_{\text{scaled}}$$z^​=zrounded​−zscaled​.detach+zscaled​

这允许梯度在反向传播期间通过四舍五入操作。最后，对于扩散模型，量化隐变量通过除以半宽进行归一化：

$$z_q = z_{\hat{}} / \text{halfWidth}$$zq​=z^​/halfWidth

此归一化确保量化隐变量保持在 $[-1, 1]$[−1,1] 范围内，与输入分布一致。

实验

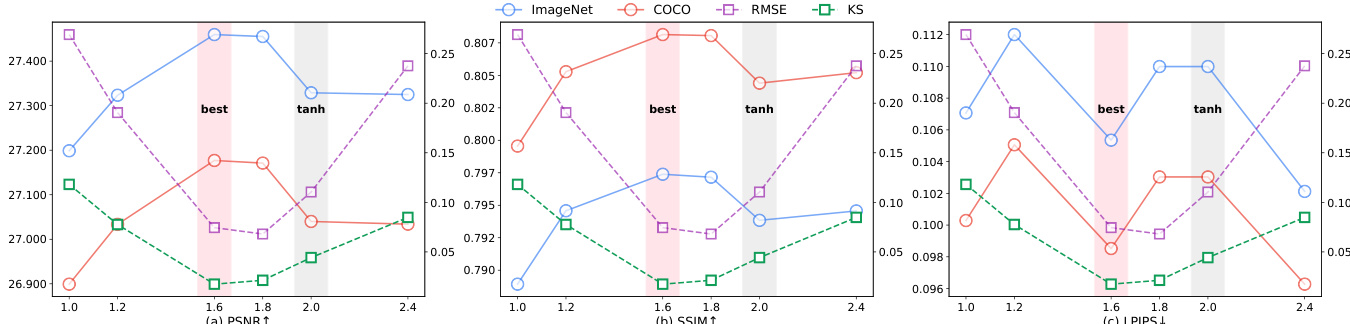
• 通过在基于 sigmoid 的激活中设置 α=1.6，优化的 iFSQ 实现近似均匀的输出分布，相比 tanh（α=2.0）显著降低 RMSE 和 KS 指标，提升重建保真度和熵利用率。
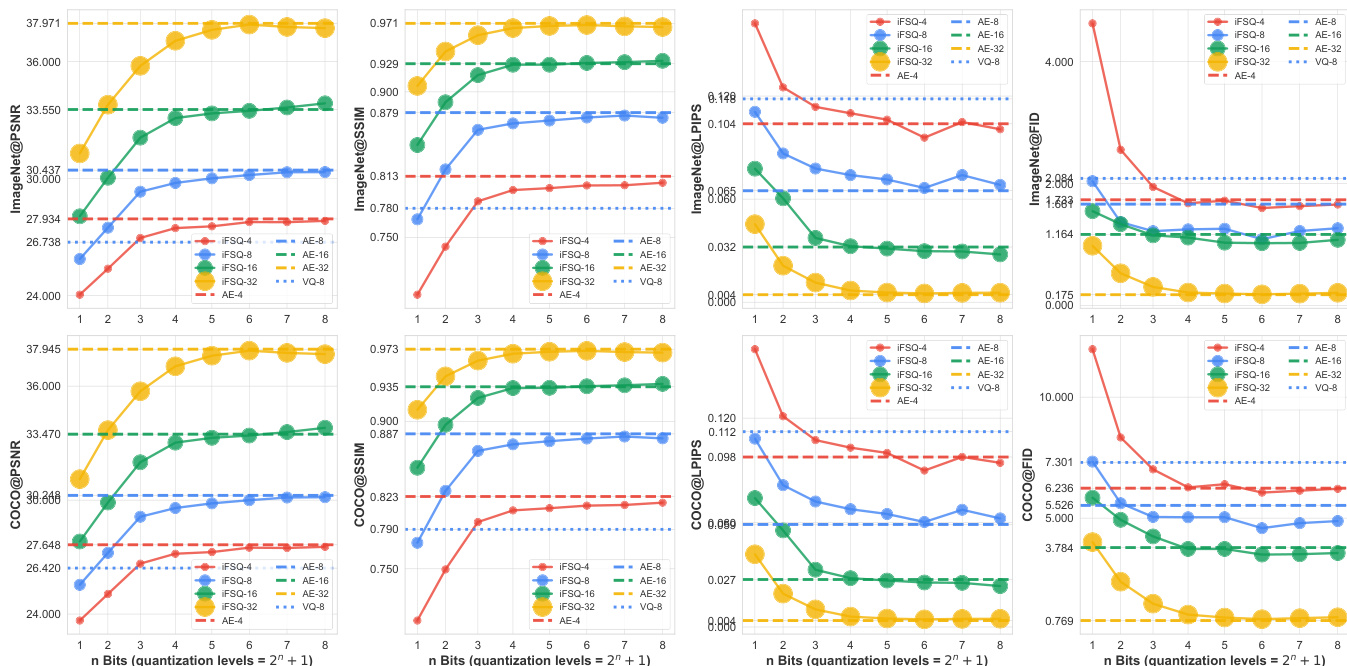
• 在 ImageNet 上，iFSQ（α=1.6）在 PSNR、SSIM 和 LPIPS 上优于 FSQ；在 COCO 上趋势一致，证实其可扩展性。
• 对于扩散生成（DiT），iFSQ 在 4 位时实现 gFID 12.76（对比 AE 的 13.78），压缩率提高 3 倍（96 对 24）；性能在 4 位后趋于稳定。
• 对于自回归生成（LlamaGen），iFSQ 在相同隐维度和更低比特率下优于 VQ；4 位 iFSQ 与 AE 相当，性能在 4 位达到峰值。
• iFSQ 实现扩散与 AR 模型的公平比较：扩散收敛较慢，但在更高计算量下 FID 超越 AR；AR 模型表现出强烈的序列约束限制。
• iFSQ 扩展性良好：2 位时，双倍隐维度超越 AE；7–8 位时，匹配或超越 AE；在所有量化级别和维度上优于 VQ。
• REPA 对齐在 1/3 网络深度（如第 8/24 层）优化 LlamaGen 中的语义获取；λ=2.0 得到最佳 FID，与 DiT 的最优 λ 不同。
• 压缩比扩展（图 10）显示线性性能趋势，最优拐点在约 48× 压缩（4 位）；VQ 与 iFSQ 趋势接近，验证其混合离散-连续特性。

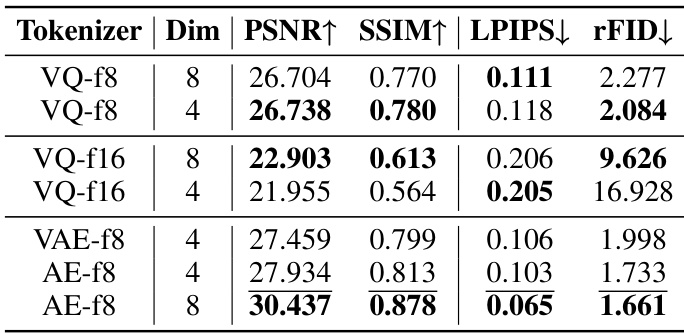
作者比较了包括 VQ 和 AE 变体在内的各种分词器，发现 AE-f8 在 PSNR 和 SSIM 上表现最佳，同时获得最低的 LPIPS 和 rFID 分数，表明其重建质量最优。在基于 VQ 的分词器中，VQ-f8 在所有指标上优于 VQ-f16，表明更高量化级别可提升重建性能。

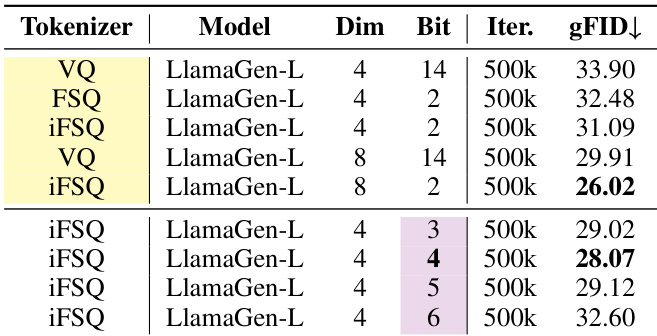
结果显示，2 位的 iFSQ 实现最低 gFID 26.02，优于相同设置下的 VQ-VAE 和 FSQ。当比特率超过 2 位时性能下降，4 位 iFSQ 的 gFID 为 28.07，表明在此配置下较低量化级别更优。

结果显示，α = 1.6 的 iFSQ 在 PSNR、SSIM 和 LPIPS 上表现最佳，优于原始 FSQ（α = 2.0），同时最小化 RMSE 和 KS 统计量，表明分布近似均匀。α = 1.6 的最优设置平衡保真度与分布对齐，相比连续和离散基线实现更优的图像重建质量。

作者使用 iFSQ 优化图像生成模型中隐特征的分布，表明将激活参数 α 设置为 1.6 可实现近似均匀分布，从而提升重建质量和生成性能。结果显示，4 位的 iFSQ 在 PSNR、SSIM 和 FID 等指标上匹配或超越连续 AE 和 VQ-VAE，同时保持更高压缩比和更好训练效率。

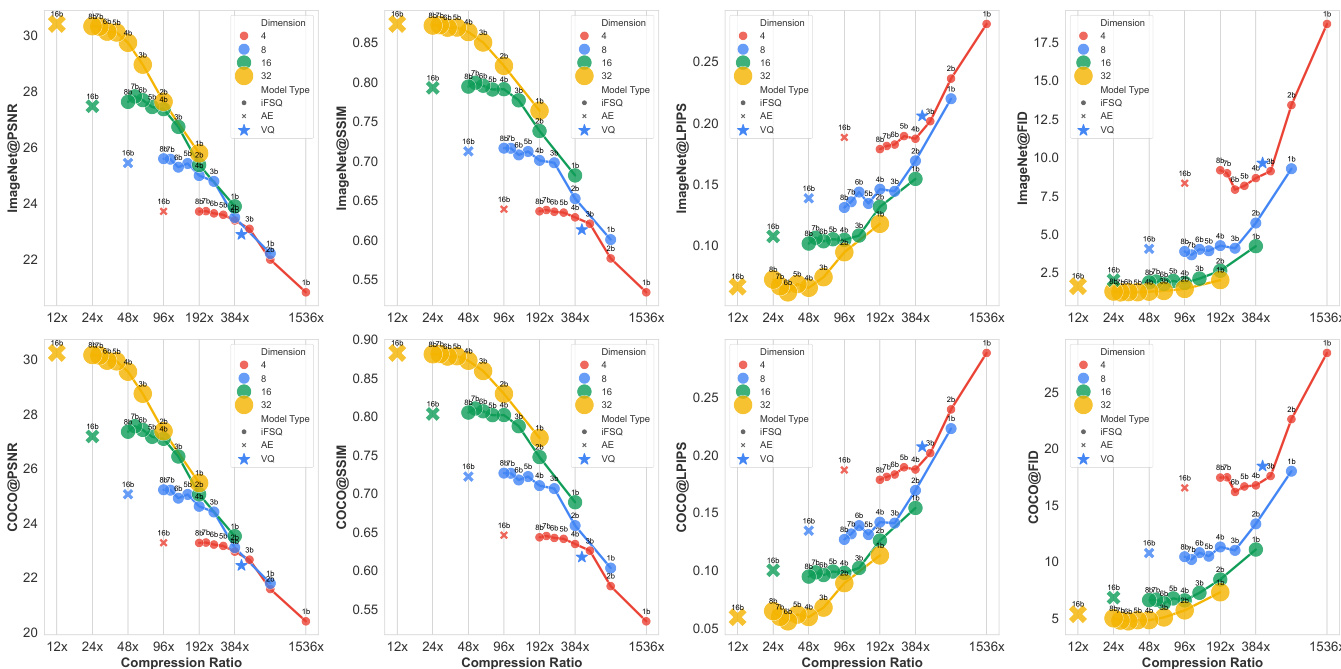
结果显示，4 位的 iFSQ 在重建与生成性能间取得最佳平衡，在 PSNR、SSIM 和 LPIPS 指标上优于 AE 和 VQ-VAE，同时保持显著更高的压缩率。4 位的最优性能与理论分析一致，其中 iFSQ 激活分布最接近均匀分布，最大化信息熵并最小化激活坍塌。