一句话总结

西安交通大学与南洋理工大学的研究者提出MAXS，一种用于大语言模型（LLM）智能体的元自适应推理框架，通过引入前瞻规划与轨迹收敛机制，缓解局部短视与推理不稳定性问题，结合优势估计与一致性驱动的步长选择，实现高效、稳定且高性能的多工具推理。

主要贡献

• 现有LLM智能体方法因缺乏前瞻规划且对早期错误敏感，导致局部短视生成与轨迹不稳定性，阻碍了多工具任务中全局推理有效性与计算效率之间的平衡。
• MAXS提出一种元自适应推理框架，采用轻量级前瞻策略估计工具使用价值，并结合步长一致性方差与步间趋势斜率，实现稳定且高价值的步长选择，有效缓解短视与不稳定性问题。
• 在三个LLM主干模型与五个数据集上的实证评估表明，MAXS在任务准确率与推理效率方面均持续优于基线方法，消融实验进一步验证了其前瞻机制与收敛机制的关键作用。

引言

大语言模型（LLM）智能体通过动态整合搜索、代码执行等工具融入推理流程，已成为复杂问题求解的核心。然而，现有方法面临两大关键挑战：局部短视决策，即工具使用缺乏前瞻性；轨迹不稳定性，即早期错误因刚性、逐级推理路径而持续传播。尽管Tree of Thought与蒙特卡洛树搜索等方法提升了全局规划能力，但其因遍历所有路径而带来高昂计算成本。本文作者提出MAXS，一种元自适应探索框架，使LLM智能体能够通过估计未来工具使用的价值，实现轻量级的前瞻推理。通过结合步长一致性方差与步间趋势分析，MAXS选择稳定且高价值的推理步骤，并采用轨迹收敛机制，在一致性达成时提前终止推理过程。该方法在保证全局有效性的同时实现计算高效，优于先前多种方法，在多个基准测试中表现更优，且显著降低token消耗。

数据集

• 数据集包含五个公开可用的基准：MathVista、Olympiad-Bench、EMMA、TheoremQA与MATH，均用于评估大语言模型在多学科、多难度层级下的多样化科学推理能力。

• MathVista（testmini子集）包含1,000个数据点，涵盖代数、几何、统计、科学、数值常识与逻辑推理任务，难度各异，用于评估综合科学问题求解能力。

• Olympiad-Bench提供6,728道来自数学与物理奥林匹克竞赛的开放性问题，覆盖竞赛级与大学级挑战；作者仅选取开放性问题以聚焦生成式推理，排除定理证明类题型。

• EMMA在每个子领域（数学、物理、化学）提供100个数据点，融合数学表达式、物理公式与化学符号与自然语言，用于测试跨学科推理能力。

• TheoremQA包含800组高质量问答对，基于数学、物理、工程、计算机科学与金融领域超过350个唯一定理，强调在问题求解中对形式化定理的应用。

• MATH包含12,500道高中竞赛级题目，来自AMC、AIME等考试，覆盖七个领域：预代数、代数、数论、计数与概率、几何、中级代数与微积分预备。作者从中采样300道题——每五种难度各60道，以确保难度层级的均衡覆盖。

• 数据用于训练混合数据集，其比例根据模型表现动态调整，以支持在多种推理类型与难度层级上的有效学习。

• 所有数据集仅进行最小预处理：原始文本被清洗，答案从逐步解题中提取。原始数据未进行裁剪，但MATH子集按难度层级进行均匀采样，以保障训练平衡。

• 保留主题标签、难度评级与问题领域等元数据，用于指导训练与评估，支持细粒度性能分析。

方法

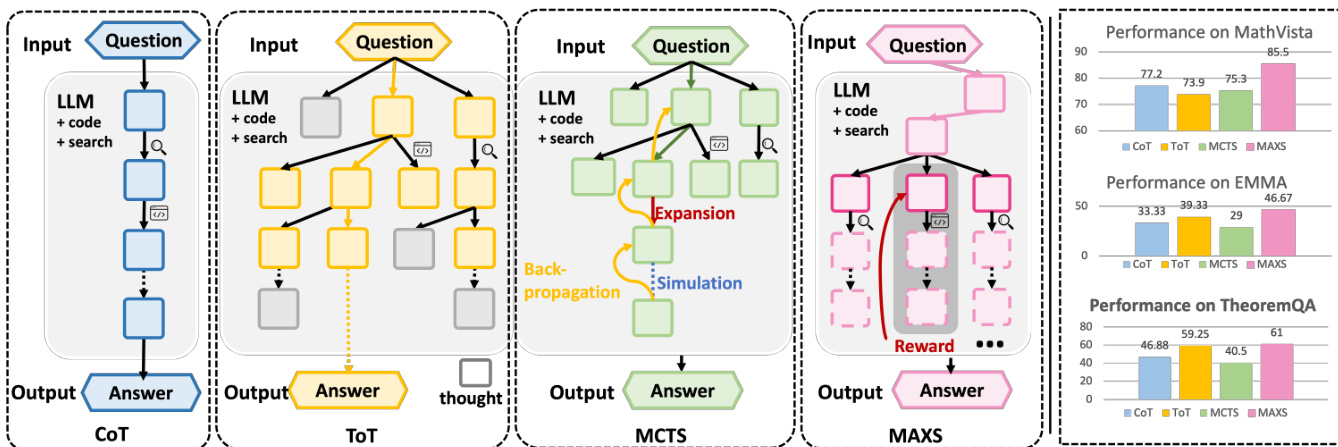
作者提出一种元自适应推理框架MAXS，旨在提升大语言模型（LLM）智能体在多工具推理任务中的决策能力。整体架构如框架图所示，采用迭代过程：智能体根据输入问题及其历史生成推理步骤。在每一步，MAXS执行三阶段流程以选择最优下一步动作：前瞻滚动生成、价值估计与整合步骤。流程始于输入问题，由LLM智能体处理。智能体可在特定步骤调用外部工具（如代码解释器或搜索引擎）以增强推理能力。过程持续进行，直至生成最终答案。

第一关键组件是前瞻策略，用于解决局部短视生成问题。该策略模拟未来若干步的推理路径，以估计当前步骤的长期价值。如图所示，智能体从当前状态 $s_i$si​ 生成一组候选未来轨迹，期望回报 $R(s_{>i})$R(s>i​) 通过未来奖励的折现和递归估计，符合贝尔曼最优性原理。这种前瞻性使智能体的决策不仅基于即时收益，更考虑其对全局更优解的潜在贡献。当前步骤的选择基于对未来的价值估计，将前瞻信息融入策略中。

第二组件是复合价值估计机制，旨在缓解轨迹不稳定性。该机制通过结合三个不同评分来评估候选推理轨迹。第一个是优势评分，衡量前瞻概率相比上一步的相对提升。第二个是步级方差评分，量化未来步骤对数概率的波动程度。较低方差表示轨迹更稳定一致，类比于动力系统中的李雅普诺夫稳定性。第三个是斜率级方差评分，通过分析对数概率一阶差分的方差，衡量轨迹方向演进的平滑性。较低斜率方差意味着路径更具Lipschitz连续性，避免突变。这三个评分整合为统一奖励函数，用于指导下一步推理步骤的选择。

第三组件是轨迹收敛机制，用于控制计算成本。该机制监控生成轨迹的一致性。当候选路径的复合奖励方差低于预设阈值时，滚动生成过程提前终止。这使框架在全局有效性与计算效率之间取得平衡，一旦识别出稳定且高价值路径，即可避免不必要的滚动生成。完整的解码过程如算法所示，迭代执行该三阶段流程，直至生成序列结束标记。

实验

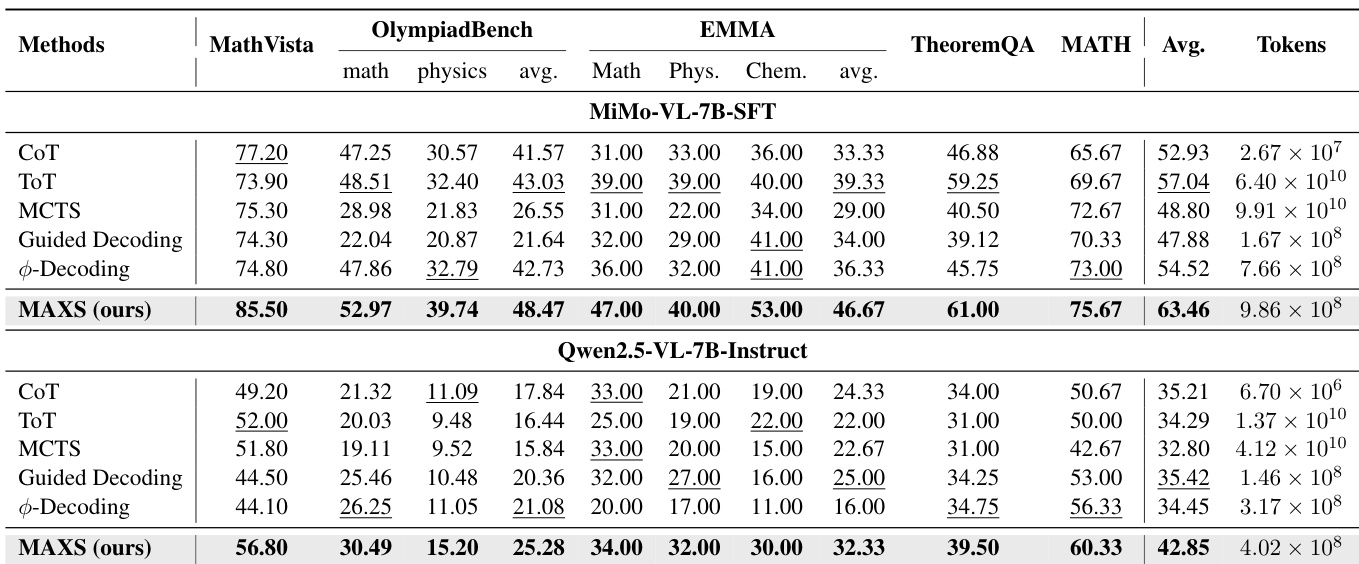
• MAXS在五个推理基准（MathVista、OlympiadBench、TheoremQA、MATH、EMMA）上，使用三种多模态LLM主干（MiMo-VL-7B、Qwen2.5-VL-7B、Qwen2.5-VL-32B）均达到最先进性能，其中在MiMo-VL-7B上准确率达63.46%，较ToT高出6.42%，较Guided Decoding高出7.43%。
• MAXS展现出更优的准确率-成本权衡：在MiMo-VL-7B上，以1,000倍更少的token实现49%准确率，相较MCTS显著降低消耗；在相似计算成本下，较φ-Decoding提升近8%。
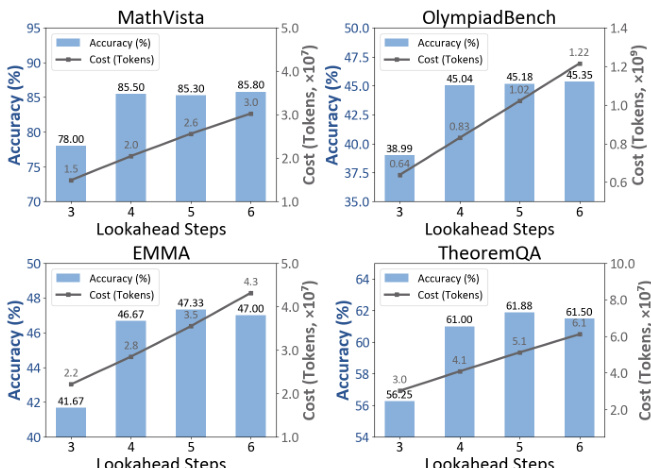
• 4步前瞻提供最佳平衡——准确率在4步后趋于平稳，而token使用量在4步后急剧上升，确认其为效率前沿。
• 基于方差的早期停止机制（δ = 0.002）实现轨迹收敛，显著降低推理成本，且不牺牲准确率，支持高效滚动生成。
• 消融实验表明，前瞻机制对全局推理至关重要（Qwen2.5-VL-7B上下降9.44%），优势评分是主导奖励成分。
• 代码与搜索工具具有互补性：移除任一均损害性能，其中代码工具对符号推理尤为关键（如MathVista上下降14.7%）。
• 价值估计中α = 0.3与β = 0.2时达到峰值准确率（63.5%），较仅使用优势的基线提升+8.3%，较基于对数概率的方法提升5.0–10.3%。
• 多数问题在4–8步内解决，验证13步上限的合理性，OlympiadBench需更深层次推理。
• 1-beam解码在效率与准确率之间取得最佳平衡，更大beam宽度带来的收益递减。
• McNemar检验确认MAXS的提升在所有基线与模型架构上均具有统计显著性（p < 0.001）。
• 一个失败案例揭示：当基于工具的检索存在不确定性时，早期误识别可能导致错误传播，尽管下游计算正确。

作者采用轨迹收敛机制，在候选奖励方差低于阈值时终止滚动生成，提升推理效率而不牺牲稳定性。结果表明，MAXS在准确率上优于ToT、MCTS等基线，同时显著减少token使用，展现出性能与计算成本之间更优的权衡。

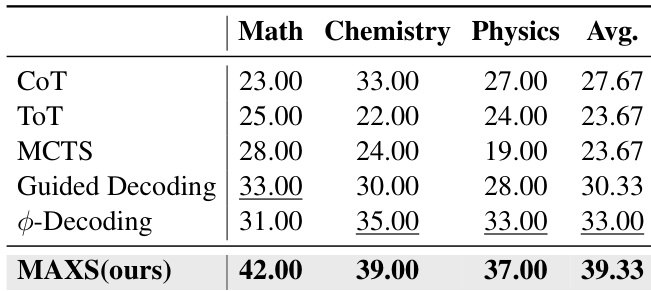
作者使用MAXS在所有基准上实现最高平均准确率，显著优于CoT、ToT、MCTS与Guided Decoding等基线方法。结果显示，MAXS平均准确率达39.33%，较次优方法Guided Decoding高出6.00个百分点。

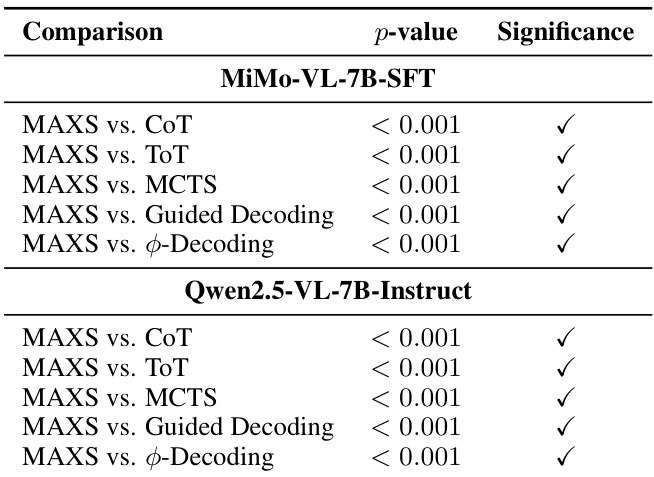
作者使用McNemar检验评估MAXS在两个模型（MiMo-VL-7B-SFT与Qwen2.5-VL-7B-Instruct）上对五种基线的统计显著性。结果显示，MAXS在所有对比中均取得统计显著提升，p值均小于0.001。

结果显示，4步前瞻在所有数据集上均实现准确率与效率的最佳平衡。准确率从3步增至4步后趋于平稳，而token使用量在4步后急剧上升，确认进一步前瞻带来的收益递减。

作者使用MAXS在多个推理基准上实现最先进性能，优于ToT与Guided Decoding等基线方法，在MiMo-VL-7B与Qwen2.5-VL-7B模型上均表现更优。结果显示，MAXS在显著更低的计算成本下实现更高准确率，相比MCTS等树状方法最多减少100倍token消耗，同时保持强效率。