一句话总结

宾夕法尼亚大学与微软研究院的作者提出了一种名为“多路思维”（Multiplex Thinking）的随机连续推理框架，该框架在每一步采样 $K$K 个离散标记，将其嵌入向量聚合为单一的多路标记，并通过保留概率语义实现策略内强化学习。与确定性连续方法不同，它保持基于采样的随机性以实现有效探索，在数学推理基准测试中，以更短、更高效的轨迹表现优于离散思维链（CoT）和强化学习基线。

主要贡献

• 我们提出了“多路思维”（Multiplex Thinking），一种标记高效的推理框架，通过独立采样将多个离散推理候选压缩为单一连续的多路标记，保留随机性，支持广度优先探索，同时减少序列长度。

• 该方法通过分解采样标记的似然性，对完整推理轨迹建立了明确定义的概率分布，允许在无需高成本生成完整离散 CoT 的情况下，直接对多路 rollout 进行强化学习优化。

• 实验结果表明，在数学推理基准测试（Pass@1 到 Pass@1024）中，多路思维持续优于离散 CoT 和强化学习基线，通过有效压缩高熵推理步骤，实现了更高的准确率和更短、更紧凑的推理轨迹。

引言

大型语言模型（LLMs）在数学与逻辑任务中展现出强大的推理能力，通常通过思维链（CoT）提示生成显式的中间步骤。尽管强化学习（RL）可通过优化 CoT rollout 进一步提升推理性能，但两种方法均因需要长而离散的标记序列而成本高昂——通常以深度优先方式解码，限制了探索能力。现有的连续推理方法通过在单个连续标记中编码多条路径来降低标记成本，但通常是确定性的，会破坏对策略内强化学习和探索至关重要的随机性。

为解决此问题，作者提出“多路思维”（Multiplex Thinking），一种基于采样的连续推理框架，在保持随机性的同时实现紧凑高效的推理。在每一步，它从模型输出分布中采样 $K$K 个离散标记，将其映射为嵌入向量，并聚合为单一的多路标记。该设计保留了离散采样的概率结构，在高熵推理阶段支持丰富的多路径编码，并通过因子化概率模型实现对完整 rollout 的直接强化学习优化。

该方法在数学基准测试（Pass@1 到 Pass@1024）中持续优于离散 CoT 和强化学习基线，准确率更高且响应长度更短，证明了随机连续推理能够弥合效率与有效探索之间的差距。

数据集

• 数据集包含多个文本来源，包括网络爬取内容、书籍、学术论文以及精心筛选的问答对，旨在支持多样化的推理与语言任务。
• 数据集分为三个主要子集：
  • 网络文本：12 亿标记，来自公开可访问的网页，通过自动化质量评分和去重过滤，确保可读性与相关性。
  • 书籍语料库：3 亿标记，来自数字化书籍，按语言多样性与事实准确性筛选，内容已标准化以保证格式一致。
  • 问答对：5000 万标记，来自专家标注的问答数据集，包括 SQuAD、Natural Questions 和精心构建的推理基准，已过滤掉低质量或模糊条目。
• 作者在训练过程中混合使用这些子集，动态调整采样比例：早期阶段为 60% 网络文本、30% 书籍语料库、10% 问答对；后期阶段调整为 50%、40%、10%，以强调事实一致性。
• 所有文本通过共享词汇表的分词管道处理，序列截断或填充至最大长度 2048 标记。
• 采用裁剪策略以确保批次间输入长度均衡，较长序列随机裁剪至 2048 标记，同时保持语义连贯性。
• 预处理阶段构建了源类型、领域类别和质量评分等元数据，用于指导采样与训练动态。
• 训练集采用 90-5-5 比例划分：90% 用于训练，5% 用于验证，5% 用于测试，各子集无重叠。
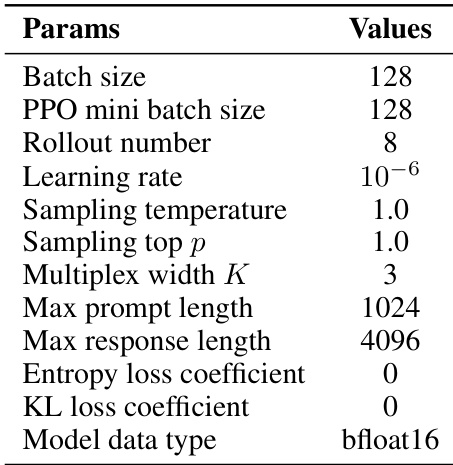
• GRPO 训练的超参数（包括学习率、批量大小、熵系数）详见表 6，并针对不同任务优化收敛性与性能。

方法

作者采用一种名为“多路思维”的新型推理范式，将连续表示的信息密度与离散采样的概率结构相结合。该框架分为两个主要阶段：分支（Branch）与合并（Merge）。在每一步推理中，模型执行独立采样，从语言模型输出分布中根据提示和先前推理步骤采样 $K$K 个离散标记。这些采样标记随后通过其嵌入的加权平均聚合为单一连续的多路标记。该聚合过程旨在保留词汇嵌入先验，维持标准离散生成的采样动态，同时通过强化学习实现可处理的优化。

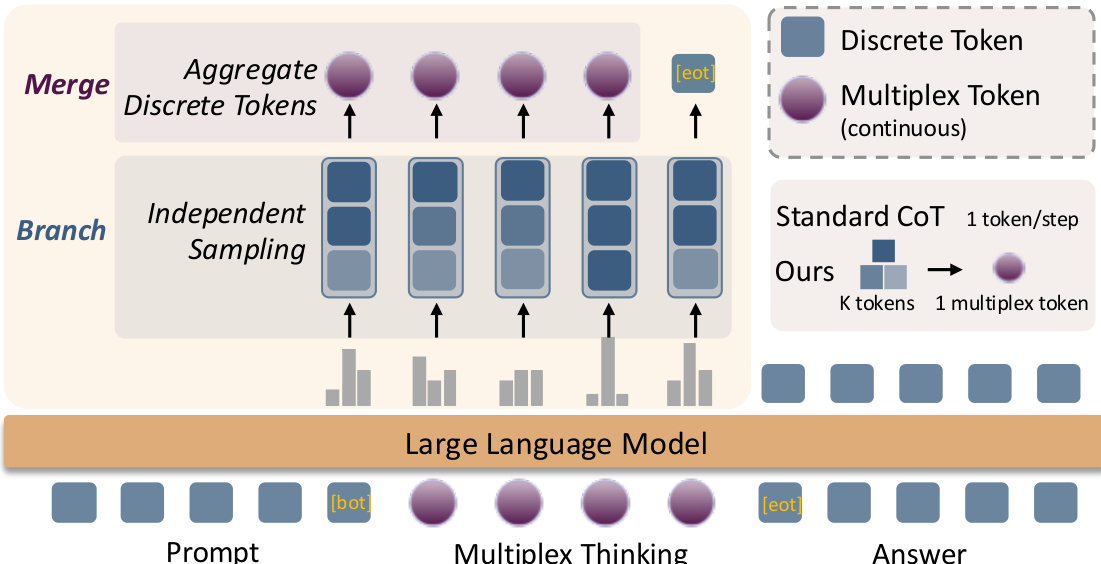
如图所示，分支阶段在每一步采样 $K$K 个离散标记，随后传递至合并阶段。在合并阶段，这些离散标记通过加权方案聚合为连续的多路标记，权重可为均匀平均，也可基于模型语言模型头的概率进行重加权。生成的多路标记作为输入送入大语言模型，用于下一步推理。该过程持续进行，直至模型生成停止标记，最终输出答案。该框架设计为自适应：当模型自信时，多路标记表现如标准离散标记；当不确定时，它能紧凑表示多个合理后续步骤，而无需增加序列长度。该设计允许使用策略内强化学习高效优化推理轨迹，因为生成多路标记的概率可分解为各组成离散样本对数概率之和。

实验

• 多路思维通过多路标记中更高的熵验证了增强的探索能力，其熵随多路宽度 $K$K 线性增长，使有效搜索空间从 $|V|$∣V∣ 扩展至 $|V|^K$∣V∣K，从而在推理轨迹中保持概率多样性。
• 在六个数学推理基准（AIME 2024、AIME 2025、AMC 2023、MATH-500、Minerva Math、OlympiadBench）上，多路思维在 12 个设置中的 11 个达到最佳 Pass@1 准确率，超越离散 CoT、离散 RL 和随机软思维基线，7B 模型在所有任务中均表现突出。
• 多路思维展现出更优的测试时扩展性，Pass@1024 性能显著优于离散基线——例如在 AIME 2025 上（7B 模型）达到约 55%，而离散 RL 仅为 40%，表明其在困难、稀疏解任务中具有更强的探索潜力。
• 该方法以更短响应长度实现更高准确率：多路思维-I 使用 4k 标记即可达到或超过离散 CoT 使用 5k 标记的性能，表明其信息密度更高，样本效率更优。
• 消融研究证实多路表示具有内在优势：多路思维-I（仅推理）优于离散 CoT，且与随机软思维相当；不同聚合策略（加权 vs. 无权）表现相似，表明对设计选择具有鲁棒性。
• 熵分析显示，多路模型在训练过程中政策熵下降更少，表明探索能力持续，提前承诺减少，这与更高的 Pass@k 上限相关。
• 定性分析表明，多路思维能动态调节探索，在高熵决策点通过将分歧候选压缩为多路标记来保留不确定性，从而在关键推理步骤实现分支行为。

作者分析了不同多路宽度下的训练熵减少情况，显示 $K=2$K=2 的多路训练熵减少最低，仅为 5.82%，表明相比离散 RL 基线（$K=1$K=1，熵减少 9.44%）具有更持久的探索能力。当多路宽度增至 $K=3$K=3 和 $K=6$K=6 时，熵减少分别上升至 6.03% 和 7.09%，表明更大宽度导致更大熵坍缩，但仍低于离散基线。

作者将不同序列长度的离散 CoT 与固定 4k 标记预算的多路思维-I 进行性能比较。结果表明，多路思维-I-4k 的平均准确率达到 40.5%，高于离散 CoT-5k 的 39.6%，证明多路标记可在更短序列中实现更优性能。这表明多路标记更高的信息密度使推理更高效，无需更长的 rollout。

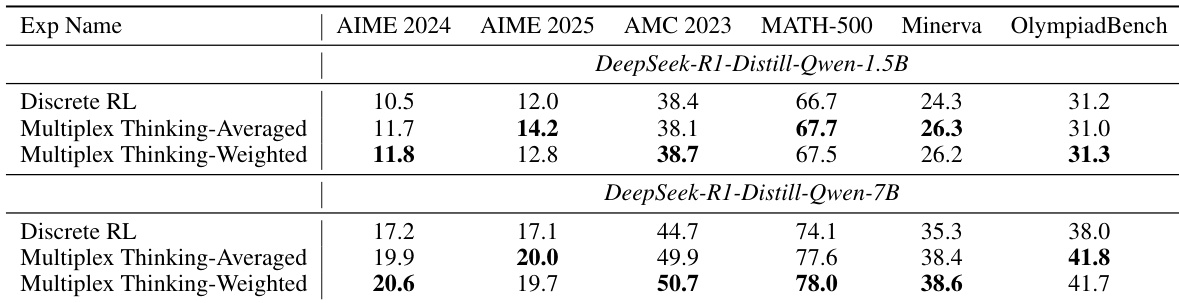
作者比较了多路思维与离散 RL 在两种模型规模和五个数据集上的 Pass@1 准确率。结果表明，多路思维在多数设置中持续优于离散 RL，尤其在 7B 模型上取得最大提升。

作者在实验中采用多路宽度 $K=3$K=3，这与消融研究中观察到的最优性能一致。该设置在探索与效率之间取得平衡：继续增加 $K$K 超过 3 会带来边际收益递减，同时相比离散基线保持更高的每标记信息密度。

作者使用表格比较多路思维在六个数学推理基准上与离散 CoT、随机软思维和离散 RL 的 Pass@1 准确率。结果表明，多路思维在 12 个实验设置中的 11 个达到最高 Pass@1 性能，对两种模型规模均持续优于所有基线。