一句话总结

来自MIT、NUS、耶鲁大学和NTU的研究者提出了一种独特性感知强化学习（Uniqueness-Aware Reinforcement Learning），该方法在rollout层面设计目标函数，通过基于大语言模型（LLM）的聚类与逆聚类规模重加权，奖励稀有的高层次推理策略，从而在不牺牲pass@1的前提下，显著提升数学、物理和医学推理基准上的解法多样性与pass@k性能。

主要贡献

• 大语言模型的强化学习常面临探索坍缩问题：策略收敛到少数主导性推理模式，尽管pass@1有所提升，但解法多样性不足，导致pass@k难以提升；本文识别出根本原因在于词元级正则化与复杂推理任务中策略级多样性需求之间的错配。
• 研究者提出独特性感知强化学习，一种基于rollout层面的目标函数，利用基于LLM的裁判对多个解法尝试按高层次策略进行聚类，并根据聚类规模反向重加权策略优势，以奖励稀有且正确的解法路径，同时降低冗余路径的权重。
• 在数学、物理和医学推理基准上评估，该方法在大规模采样预算下持续提升pass@k，并在不牺牲pass@1的前提下提高AUC@k，证明了其在探索能力与人类标注解法策略覆盖范围上的显著增强。

引言

后训练大语言模型（LLMs）的强化学习（RL）对于提升复杂推理能力至关重要，但常面临探索坍缩问题——策略收敛至少数主导性推理模式，虽提升pass@1，却因解法策略多样性不足而无法有效提升pass@k。先前方法尝试通过词元级多样性信号（如熵奖励或嵌入距离）缓解此问题，但这些方法无法捕捉高层次策略差异，将表面变化误认为真正多样性。本文提出独特性感知强化学习，一种基于rollout层面的目标函数，利用基于LLM的裁判将多个解法尝试按其高层次策略聚类，再以聚类规模的倒数对策略优势进行重加权。该方法奖励正确且稀有的策略，同时抑制常见策略，从而促进真正的策略级多样性。在数学、物理和医学推理基准上的评估表明，该方法在不牺牲pass@1的前提下，持续提升pass@k与AUC@k，即使在大规模采样预算下也能实现持续探索。

数据集

• 数据集包含三个学科领域的特定推理问题：数学、物理和医学，专为强化学习（RL）训练而构建。
• 数学领域采用MATH（Hendrycks et al., 2021）的难度筛选子集，从中选取8,523道Level 3–5的问题，代表更难、更复杂的题目，适用于高级推理任务。
• 物理领域数据源自MegaScience（Fan et al., 2025）的教材推理划分，从125万道基于教材的题目中随机抽取7,000个样本，确保涵盖广泛的概念性推理。
• 医学领域从MedCaseReasoning（Wu et al., 2025）中随机选取3,000个样本，该数据集共包含13.1k个病例，聚焦于与诊断决策相关的临床推理场景。
• 训练过程采用固定混合比例整合各领域子集，形成统一的多领域训练混合数据。
• 每个训练样本均采用标准化格式处理，包括结构化提示和真实答案，并在基于rollout的RL训练中使用每提示8次rollout。
• 为控制生成长度，采用裁剪策略：Qwen-2.5使用4096个新词元，Qwen-3和OLMo-3使用20480个词元，以保障训练效率同时保留上下文。
• 每个样本的元数据包含领域、问题类型和难度等级，由原始标注构建，用于指导训练与评估。
• 模型使用AdamW优化器，学习率设为5×10⁻⁷，生成时温度T = 1.0，并施加KL正则化（λ_KL = 0.001）。
• 评估在保留的基准上进行：AIME 2024&2025与HLE（数学）、OlympiadBench（物理）、MedCaseReasoning测试集（医学），所有问题均为纯文本形式。
• 性能通过pass@k与AUC@K衡量，其中AUC@K采用梯形法则计算，以总结不同推理预算下的整体表现。

方法

研究者采用基于群体的强化学习框架，扩展Group Relative Policy Optimization（GRPO），以增强大语言模型解法策略的多样性。整体方法通过重加权策略更新优势，优先奖励正确但稀有的解法策略，从而缓解探索坍缩。如框架图所示，流程始于问题输入，语言模型生成多个推理轨迹（rollouts）。这些rollouts随后通过基于LLM的分类器处理，按高层次解法思路（如几何堆积、有限差分）聚类，而非表面形式差异。分类步骤对识别解法策略的独特性至关重要。

该方法的核心在于优势计算，结合了解法质量与策略独特性。对于每个问题，策略生成$K$K个rollout，每个rollout由特定任务验证器赋予标量奖励。在标准GRPO中，rollout $p_{m,k}$pm,k​的组归一化优势为$z_{m,k} = (r_{m,k} - \mu_m) / (\sigma_m + \varepsilon)$zm,k​=(rm,k​−μm​)/(σm​+ε)，其中$\mu_m$μm​与$\sigma_m$σm​为组内奖励的均值与标准差。本文通过引入独特性权重$w_{m,k} = 1 / f_{m,k}^\alpha$wm,k​=1/fm,kα​进行改进，其中$f_{m,k}$fm,k​为rollout $p_{m,k}$pm,k​所属策略聚类的大小，$\alpha$α为控制重加权强度的超参数。该权重确保属于小规模、稀有聚类的rollout（如独特但正确的解法）获得更大的有效优势，而属于大规模、常见聚类的rollout则被降权。最终用于策略更新的优势为质量归一化项与独特性权重的乘积：$\text{advantage}_{m,k} = w_{m,k} z_{m,k}$advantagem,k​=wm,k​zm,k​。

训练目标保持与GRPO一致，将修改后的优势项用于策略梯度目标。策略参数被更新以最大化rollout的优势加权对数似然期望。该方法有效促使策略为每个问题探索并利用更广泛的高层次解法策略，而非收敛至单一主导模式。该方法设计为标准GRPO优势的即插即用替代方案，可轻松集成至现有语言模型强化学习流水线。

实验

• 在数学（AIME 2024/2025、HLE）、物理（OlympiadBench-Physics）和医学（MedCaseReasoning）领域，使用Qwen2.5-7B评估pass@k性能；我们的独特性感知RL方法（OURS）在中等至大采样预算（k ≥ 32）下持续优于指令基线与仅GRPO的SimpleRL，表现出更高的渐近准确率与更优的pass@k增长斜率。
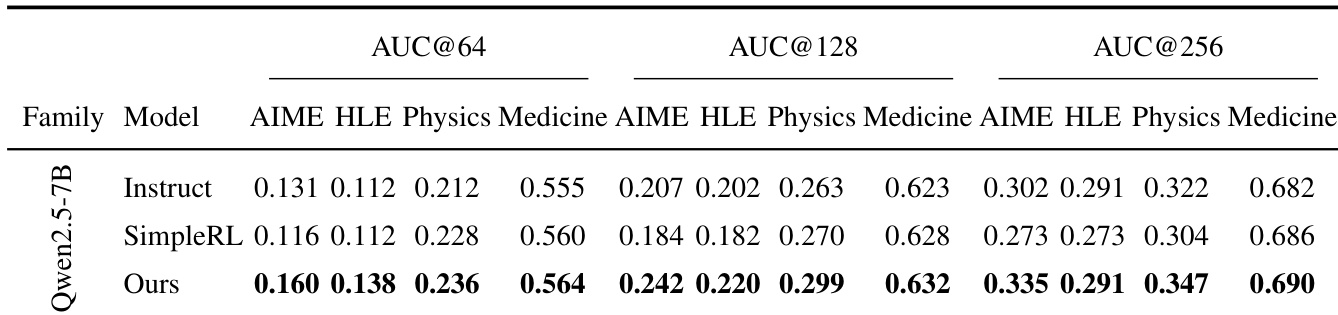
• 在Qwen2.5-7B上，OURS在所有领域与预算（K=64/128/256）下均取得最高AUC@K，尤其在挑战性AIME与HLE设置中提升显著（如AIME上K=128时+0.058），表明其具备更优的准确率-覆盖权衡与更低的模式坍缩风险。
• 在OLMo-3-7B与Qwen-3-8B上，OURS在HLE/物理基准上再次取得最佳AUC@K，优于其他探索方法（DAPO、Forking Token），证明其泛化能力及与独特性感知训练的互补优势。
• 通过熵动态分析验证持续探索能力：OURS在训练过程中保持更高且更稳定的策略熵，而SimpleRL熵持续下降，表明其解法轨迹多样性得以维持。
• 引入cover@n以衡量人类解法覆盖度；在20个挑战性AIME问题上，OURS在4个复杂问题上优于指令基线，包括在一道几何题中实现100%覆盖（通过恢复稀有策略如Symmedian Similarity），在一道组合题中实现75%覆盖（通过引入Trail/Flow Viewpoint）。

研究者使用AUC@K评估不同模型与领域间的准确率-覆盖权衡，更高值表示更优性能。结果表明，所提方法（OURS）在Qwen2.5-7B模型上，于所有预算（64, 128, 256）与领域（AIME, HLE, Physics, Medicine）中均取得最高AUC@K，显著优于指令基线与SimpleRL基线，尤其在更具挑战性的AIME与HLE设置中提升最为明显。

研究者使用AUC@K评估不同模型与方法间的准确率-覆盖权衡。结果表明，其独特性感知RL方法（OURS）在OLMo-3-7B与Qwen-3-8B模型上，于HLE与Physics基准上均取得最高AUC@64与AUC@128，显著优于指令基线与SimpleRL基线，最大提升出现在更具挑战性的HLE设置中。