一句话总结

来自香港大学、密歇根大学、爱丁堡大学、加州大学圣塔芭芭拉分校、俄亥俄州立大学以及加州大学洛杉矶分校的作者提出 MMFORMALIZER——一种新颖的多模态自动形式化框架，通过将自适应定位与感知原语相结合，递归构建在数学和物理公理上具有形式化基础的命题，实现对经典力学、相对论、量子力学和热力学等领域的机器推理，并在 PHYX-AF 基准上展示了可扩展性。

主要贡献

• 我们提出 MMFORMALIZER，一种多模态自动形式化框架，能够递归地将视觉和文本输入在物理与数学公理中进行定位，利用量纲分析和自适应终止机制，确保每个形式化命题都锚定在可测量的现实之中，并得到感知证据的支持。

• 该框架实现了对复杂物理理论（包括通过哈密顿推导的经典力学、相对论、量子力学和热力学）的形式化，是首个能够在这些领域实现统一多模态推理的方法。

• 我们提出 PHYX-AF，一个包含 115 个多样化样本的新基准，数据来源涵盖 MathVerse、PhyX、合成几何与解析几何，通过最小化模态间的冗余来强制实现真正的多模态推理，并证明前沿模型如 GPT-5 和 Gemini-3-Pro 在编译和语义准确性方面达到最先进水平。

引言

作者致力于解决将现实世界中的多模态输入（如图表、文本和物理场景）转化为可形式验证的数学与物理命题的挑战，这是实现复杂领域机器推理的关键步骤。以往的自动形式化研究主要集中在几何领域的符号或文本输入，依赖于固定的形式语言，难以捕捉现实现象中固有的量纲与物理约束。这些系统往往无法将抽象推理锚定在可测量的现实中，尤其是在涉及质量、能量和时间等物理量时，其经验性与量纲一致性尤为重要。为克服这一局限，作者提出 MMFORMALIZER，一种递归框架，将感知定位与量纲及公理推理整合于 Lean 定理证明器中。该框架采用自适应递归终止机制，确保每一步形式化都基于视觉证据且量纲一致，从而实现对经典力学、相对论、量子力学和热力学的形式化——这些领域此前在多模态自动形式化中均不可达。该方法在 PHYX-AF 上进行评估，这是一个新基准，通过最小化模态间冗余来强制实现真正的多模态推理，结果表明尽管 GPT-5 等大模型表现强劲，但几何与物理推理仍是重大挑战。

数据集

• PHYX-AF 基准包含 115 个精心筛选的样本，数据来源包括 MATHVERSE（Zhang 等，2024a）、PHYX（Shen 等，2025）、SYNTHETIC GEOMETRY（Trinh 等，2024）以及扩展的 ANALYTIC GEOMETRY 数据集。额外的合成数据通过基于规则的计算引擎（Hubert 等，2025）和受 AlphaGeometry 与 GenesisGeo 启发的符号推理框架（Zhu 等，2025）生成。

• 数据集划分为多个独立子集：

  • 多模态数学设定：主要来自 MATHVERSE，涵盖平面几何、立体几何与函数类别。这些问题源自真实考试情境，强调基于证明的推理以及从函数图像中求解多变量/高阶方程。
  • 解析几何：包含来自 GEOMETRY3K（Lu 等，2021）和 GEOINT（Wei 等，2025）的问题，并通过程序生成的二维与三维图形（由点、线、平面与多面体构成）进行增强。该子集测试对基于坐标系的几何与数值关系的理解。
  • 多模态物理设定：源自 PHYX 子集（占数据集的 21.7%），包含力学、电磁学、热力学与相对论的视觉场景。每个问题配有一张图像与一段文本约束，评估在感知噪声下的视觉-物理定位能力。
  • 合成几何设定：完全通过符号化流程生成，使用有限序列的声明性操作符（如点、线、圆、关联性、垂直性）构建几何构型。这些构型通过符号推理闭包与数值验证进行验证。

• 数据筛选确保仅保留那些图像对解题至关重要的问题——仅靠文本即可求解的问题被排除，以强制实现真正的多模态推理。

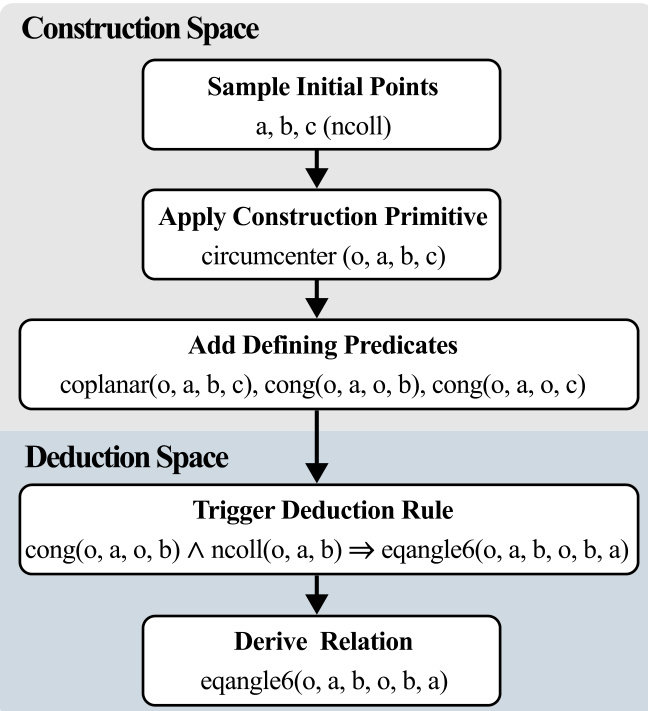
• 合成几何流程遵循四阶段过程：

  1. 合成构造：使用有限长度与对象数量的构造操作符构建几何构型，确保结构良好且非退化。无效构造（如平行线相交）被丢弃。
  2. 符号推理闭包：通过前向推理从构造中推导出所有可得的几何命题，生成完整的推导图，记录依赖关系。
  3. 最小依赖提取：选取一个推导命题作为目标，通过反向遍历推导图提取最小前提集。确保仅包含必要事实，保持推导充分性。
  4. 数值验证：每个实例使用具体实数坐标实例化。几何谓词（如相等、关联、垂直等）在固定数值容差下进行检查。失败或不稳定的实例被丢弃。

• 最终数据集用于训练与评估，混合了分布内（MATHVERSE、PHYX）与分布外（合成、解析几何）样本。模型被训练以在这些领域执行自动形式化，其中合成数据特别设计用于测试模型在测试时合成新依赖类型与构造器的能力。

• 通过结构化符号表示构建元数据，包括推导图与前提-目标依赖关系，实现对逻辑正确性与语义保真度的精确评估。所有合成实例在固定随机种子下均可复现。

方法

作者利用多模态自动形式化框架，通过 MMFORMALIZER 模型，从图像与文本等感知输入中合成形式化的类型论表示。整体架构包含三个主要归纳阶段：递归定位、递归终止与公理组合，形成一个分层流水线，将视觉与文本数据映射为形式一致的命题链。该过程始于将输入图像分解为场景图，编码原始视觉实体及其空间关系。该场景图作为基础，递归构建一个依赖形式命题的层级结构，称为 PropChain，其中每个命题均基于感知数据进行定位。

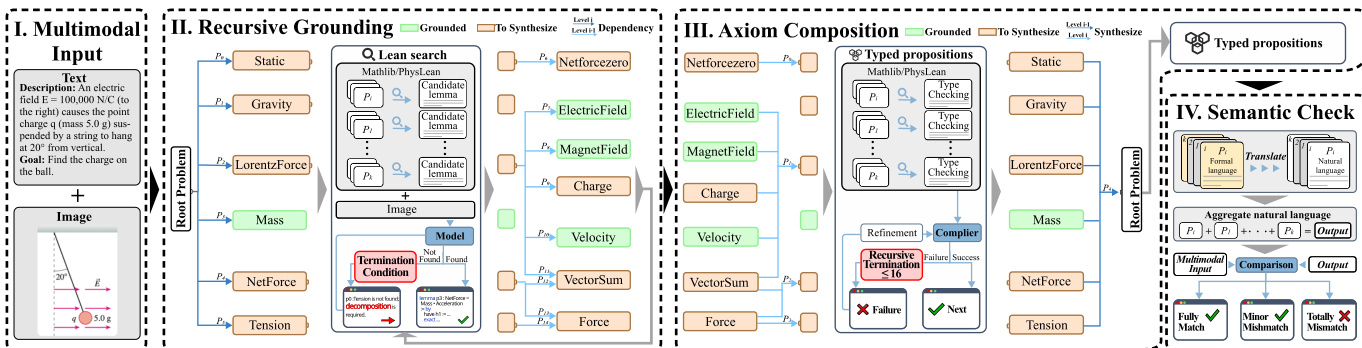
如图所示，流水线概述包含三个阶段：递归定位（识别物理原语，图中红色部分，如哈密顿量或量纲量）、递归终止，以及公理组合。图中蓝色部分表示编译器检查过程，绿色部分表示从依赖库中检索到的形式化陈述。

递归定位过程记为 $\mathsf{RG}$RG，通过将感知场景结构映射为形式命题，逐步构建 PropChain。该过程通过将场景图递归分解为一系列引理层次实现，每个引理为一个依赖对，包含一个形式命题及其证明项。定位过程始于将输入图像解析为底层场景图 $G_0$G0​，其由一系列视觉原语（如点、线或区域）及其空间关系组成。每个原语被赋予初始语义假设，构成命题结构的底层。通过结合语义搜索与大语言模型（LLM）提示，从形式化库中检索并选择最相关的定理，递归扩展定位过程。

递归终止阶段确保形式抽象既得到感知定位支持，又能约束后续解析。当命题在基本量纲量或基本公理中定位时，递归终止。该终止条件由映射函数决定，用于判断当前命题是否对应于物理量纲或形式系统中的公理。该过程分为两个主要阶段：定位阶段，使用中间引理语句在形式化库中搜索相关定理；终止阶段，当达到基本量纲或公理时停止递归。

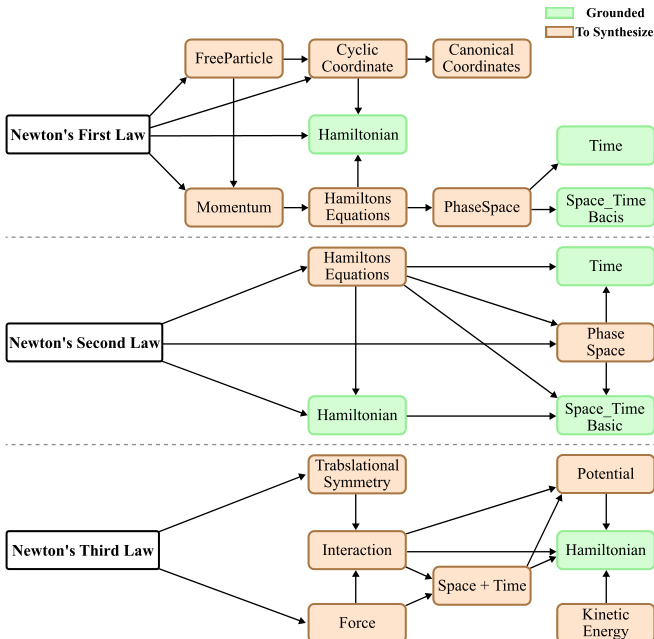
最终阶段为公理组合，构建 AxiomChain，表示命题层级的形式闭包。通过递归组合子节点为非叶节点，使用组合算子捕捉从感知子结构到层级依赖命题的过渡。生成的形式化陈述通过语法检查器进行编译验证，确保其在 LEAN 系统中的结构与逻辑有效性。该过程支持构建忠实反映物理与概念现实生成结构的形式模型，其中原语组合形成受定律约束的形式系统。

实验

• Gemini-3-Pro 在 MATHVERSE 和 ANALYTIC GEOMETRY 上达到最高编译与语义准确性，而 GPT-5 在 PHYX 上表现优异，尤其在现代类别（量子力学与相对论）中展现出更强的物理推理与定位能力。
• 所有模型在 SYNTHETIC GEOMETRY 和 ANALYTIC GEOMETRY 上的准确率显著偏低，表明视觉到形式化推理及训练分布外泛化仍存在持续挑战。
• Qwen3-VL-235B 作为最强的开源模型，在物理领域问题与分布外合成几何任务上表现不佳，凸显其与前沿模型之间的性能差距。
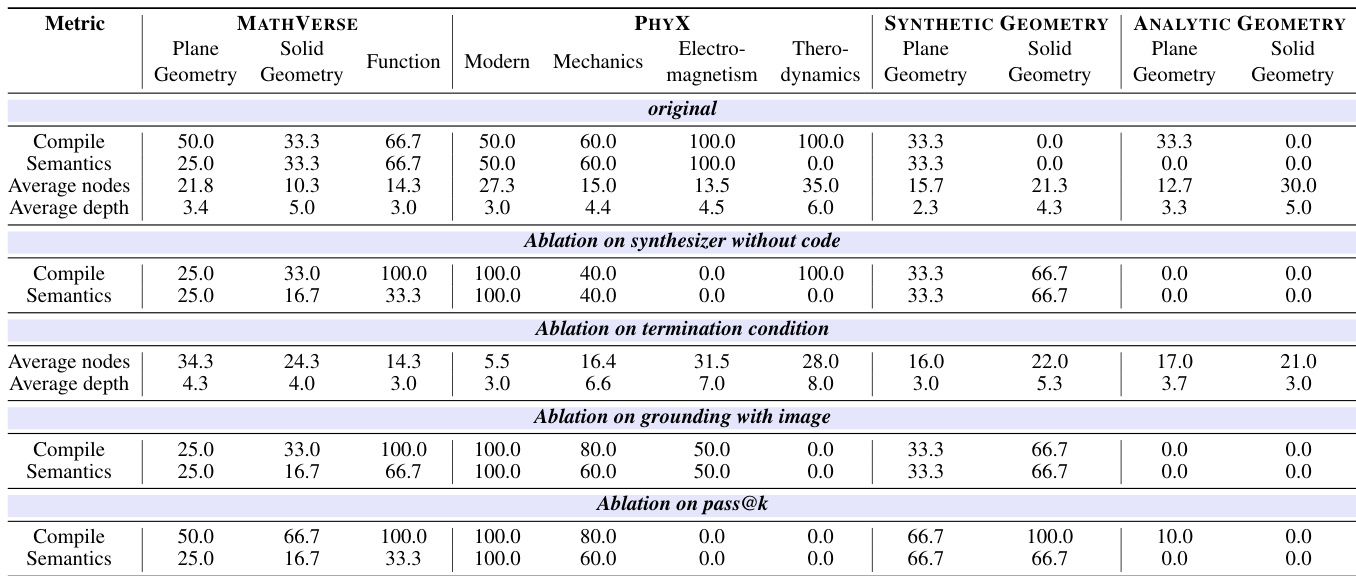
• 消融实验表明：移除检索到的参考代码可提升合成几何的分布外泛化能力；显式递归终止可防止无限分解；基于图像的定位可提升现代物理与合成几何任务的性能；增加 pass@k 可提升难题的求解效果。
• 在语义检查中，Gemini-2.5-Pro 在 MATHVERSE、PHYX 和 ANALYTIC GEOMETRY 上均达到最高准确率；Qwen2.5-VL-72B 在验证 Qwen3-VL-235B 生成代码时表现与 Gemini-3-Pro 相当，揭示弱模型监督强模型的潜力。
• 案例研究验证了该框架在复杂问题（如几何体、牛顿定律、量子隧穿、相对论速度叠加）中构建可验证依赖图与在 Lean 中执行逻辑定位的能力，失败案例凸显了终止条件的必要性。

结果表明，GPT-5 在多数基准上达到最高编译与语义准确性，尤其在 PHYX 数据集上表现突出；Gemini-3-Pro 在 MATHVERSE 与 ANALYTIC GEOMETRY 上表现最佳。所有模型在合成几何与解析几何任务上均表现不佳，表明视觉与形式化推理仍面临持续挑战，而 Qwen3-VL-235B 等开源模型与前沿模型之间存在显著性能差距。

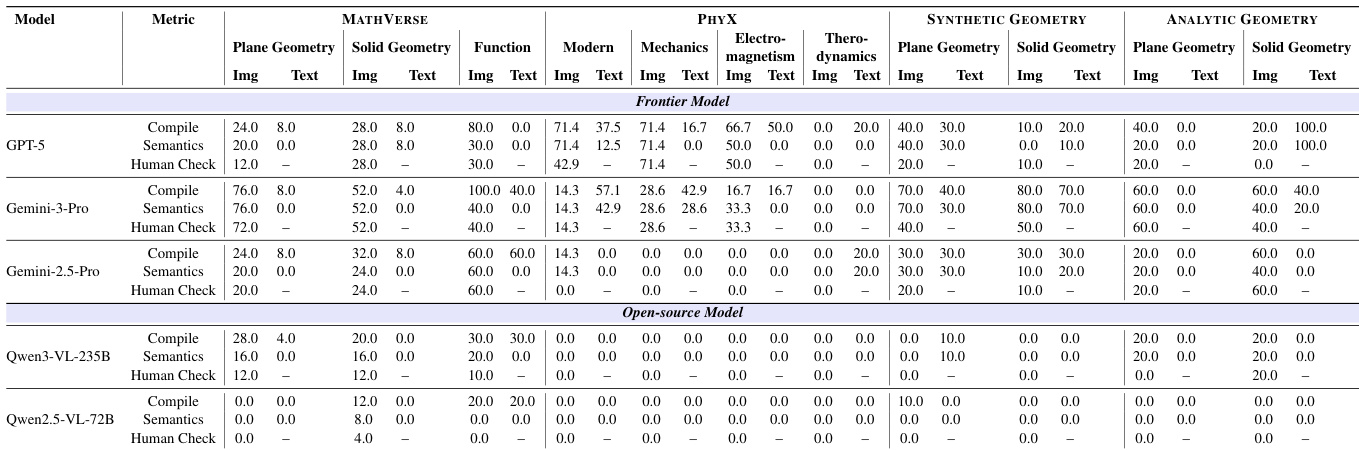
作者使用提供的柱状图展示评估基准中不同领域与子领域的问题分布情况。结果显示，MATHVERSE 占据数据集的大部分（52.2%），其中最大部分为平面几何。PHYX 占比 21.7%，主要由力学与立体几何构成。合成几何与解析几何分别占剩余的 17.4% 与 8.7%，前者以平面几何为主，后者同样以平面几何为主。

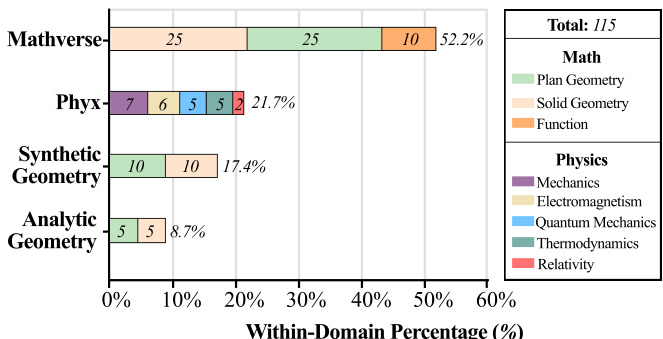
结果表明，Gemini-3-Pro 在 MATHVERSE 与 ANALYTIC GEOMETRY 上准确率最高，而 GPT-5 在 PHYX 与 SYNTHETIC GEOMETRY 上表现最佳。所有模型在合成几何任务上表现显著偏低，表明视觉与形式化推理仍面临持续挑战。

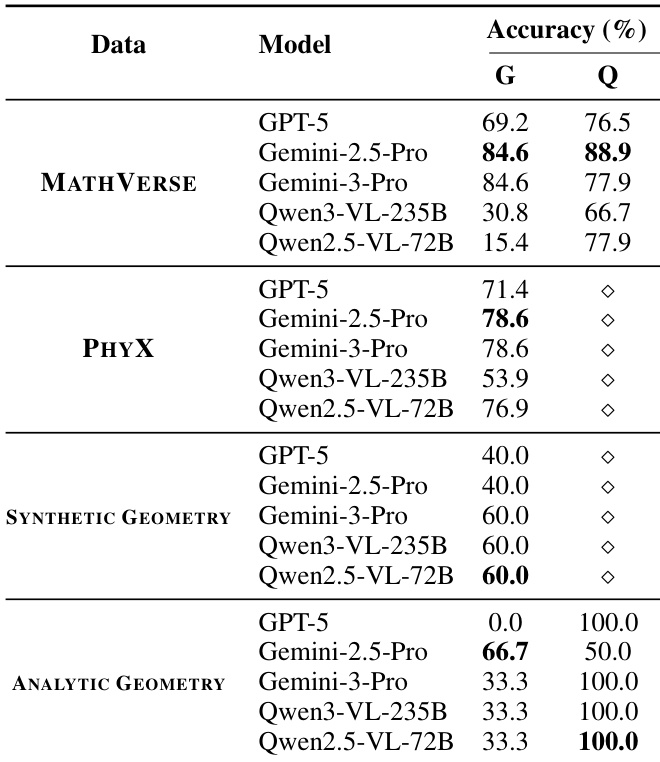
结果表明，原始模型配置在多数基准上达到最高编译与语义准确性，尤其在 PHYX 与 MATHVERSE 数据集上表现突出。消融实验显示：移除检索代码可提升分布外泛化能力；强制终止条件可防止递归过度分解；基于图像的定位可提升复杂物理与几何任务的性能；增加 pass@k 可提升难题的语义准确性，表明测试时扩展的有效性。