一句话摘要

该文作者来自密歇根大学，提出了一种基于参数化框架的新型拟牛顿方法，可直接计算受扰4D辛映射中的次谐波周期轨道（SPOs）及其Floquet向量和乘子，实现ε的高效延拓以及相关弱稳定与不稳定流形的泰勒参数化——相较于多射击法有显著改进，并在2.5自由度哈密顿系统（如天体力学中出现的系统）的共振轨道建模中展现出实用价值。

主要贡献

• 本文解决了在受扰2.5自由度哈密顿系统（如周期性扰动的2自由度流的闪烁映射）中计算长而不稳定次谐波周期轨道（SPOs）的挑战——这些轨道源于未扰系统中的共振环面，对理解由共振重叠导致的不变环面破裂至关重要。

• 作者提出一种新型拟牛顿方法，通过将参数化方法框架适配至周期轨道，同时计算SPOs、其Floquet乘子和Floquet向量，实现扰动参数ε的高效延拓，避免了传统多射击方法中典型的$O(q^3)$O(q3)线性求解开销。

• 该方法在真实天体力学问题中得到验证，包括木星-木卫一-木卫二系统中的共振轨道，并可进一步计算这些SPOs的弱稳定与不稳定流形的泰勒参数化，为研究高维辛系统中的全局动力学提供了强大工具。

引言

作者针对由周期性扰动的2自由度哈密顿系统（如天体力学中的平面圆型限制四体问题）产生的4D辛映射中长而不稳定周期轨道（即次谐波周期轨道，SPOs）的计算挑战展开研究。这些轨道对理解因次级共振导致的不变环面破裂至关重要，尤其当扰动使长周期轨道的分离子相交时，会引发混沌动力学。以往方法依赖多射击算法，需求解大型$4q \times 4q$4q×4q线性系统以同时获得轨道点及其稳定性性质，导致$O(q^3)$O(q3)计算复杂度，对大$q$q值不可行。本文主要贡献是一种新型快速多射击方法，通过将参数化方法适配至周期轨道，同时计算SPOs及其Floquet向量和乘子。该方法通过将Floquet方程直接嵌入牛顿迭代中，避免求解大型线性系统，降低计算成本并直接获得稳定性信息。该方法适用于一大类4D辛映射，并已成功应用于木星-木卫一-木卫二与天王星-泰坦尼亚-欧伯隆系统的SPOs及其分离子的计算，展示了其在空间任务设计与动力系统分析中的实用性。

方法

作者开发了一种拟牛顿方法，用于在一族4D辛映射$F_\varepsilon$Fε​中同时计算次谐波周期轨道（SPOs）及其关联的Floquet向量和乘子。该框架旨在研究SPOs从无扰映射$F_0$F0​在扰动系统中的持久性，支持以扰动参数$\varepsilon$ε为变量的数值延拓。该方法是不变环面参数化方法的改编，但专为直接计算周期轨道而设计。算法核心在于求解SPO点$X_\varepsilon(k)$Xε​(k)，$k=0,\ldots,q-1$k=0,…,q−1，以及表示Floquet向量和乘子的矩阵$P_\varepsilon(k)$Pε​(k)和$\Lambda_\varepsilon(k)$Λε​(k)。SPO的不变性方程为$F_\varepsilon(X_\varepsilon(k)) = X_\varepsilon(k+1 \mod q)$Fε​(Xε​(k))=Xε​(k+1modq)，而Floquet方程为$DF_\varepsilon(X_\varepsilon(k))P_\varepsilon(k) = P_\varepsilon(k+1 \mod q)\Lambda_\varepsilon(k)$DFε​(Xε​(k))Pε​(k)=Pε​(k+1modq)Λε​(k)。矩阵$\Lambda_\varepsilon(k)$Λε​(k)被约束为近对角形式，其中稳定与不稳定乘子$\lambda_s(k)$λs​(k)和$\lambda_u(k)$λu​(k)位于对角线上，而内部动力学乘子$\lambda_1$λ1​和$\lambda_2$λ2​位于左上角块中，可能包含非对角项$T$T。该结构使方程组可分解为一系列一维线性问题，根据乘子的谱性质，通过不动点迭代或显式公式高效求解。方法首先利用已知的无扰SPO及其单值矩阵初始化$\varepsilon=0$ε=0时的解，随后通过一系列拟牛顿步数值延拓至$\varepsilon>0$ε>0。每一步通过修正SPO点$X$X和Floquet矩阵$P$P与$\Lambda$Λ，以减小残差误差$E(k)$E(k)和$E_{red}(k)$Ered​(k)，分别衡量不变性方程与Floquet方程的违反程度。$X$X的修正由修正向量$\xi(k)$ξ(k)的线性化方程导出，而$P$P与$\Lambda$Λ的修正则由$Q(k)$Q(k)和$\Delta\Lambda(k)$ΔΛ(k)的类似方程导出。每次修正后，对更新后的$\Lambda_c(k)$Λc​(k)进行Schur分解，以确保其保持所需的近对角形式，这对数值稳定性至关重要。最终得到的SPO与Floquet向量用于计算SPO弱稳定与不稳定流形的泰勒参数化（若存在）。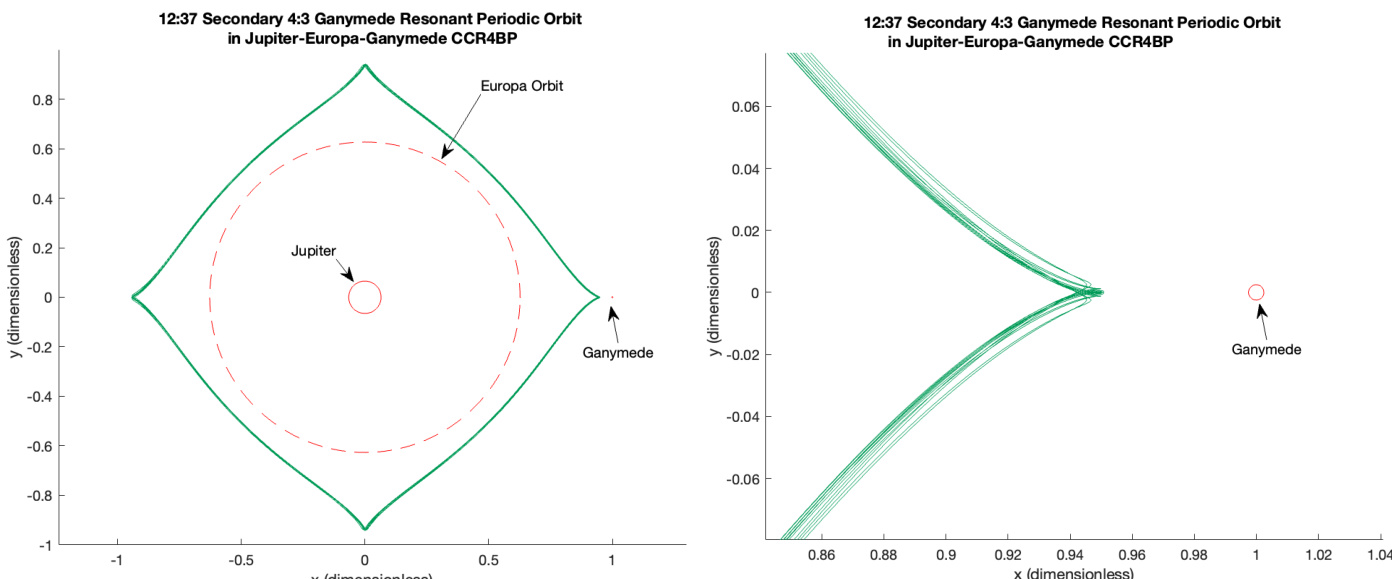

实验

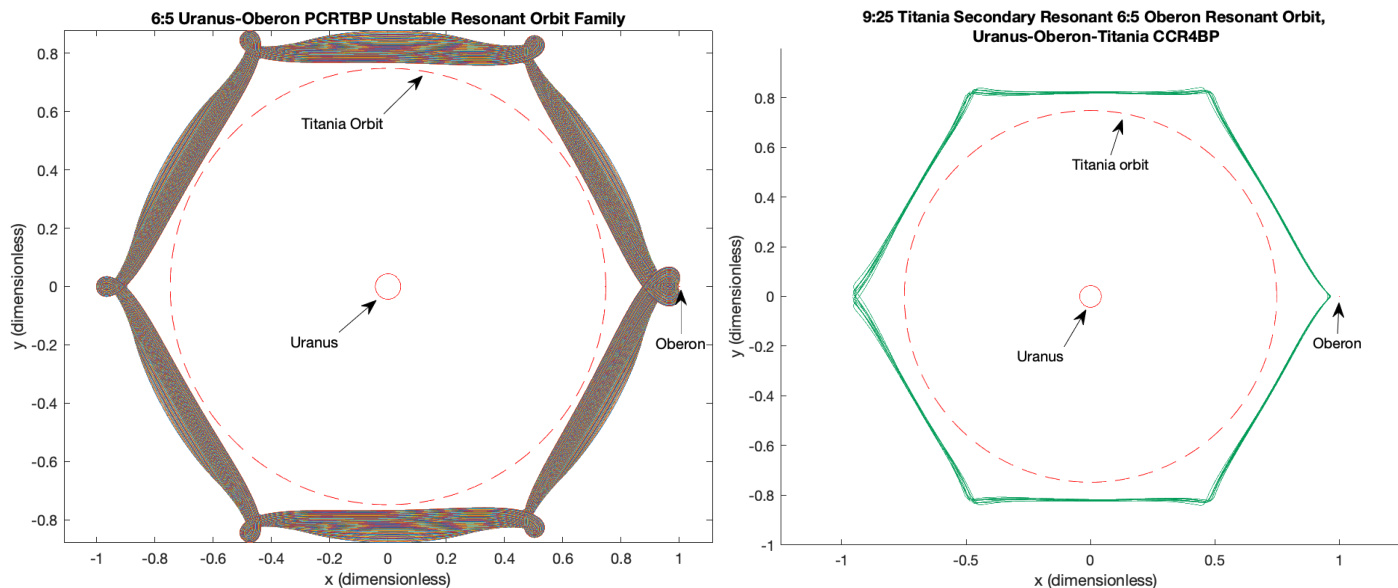
• 使用数值延拓与参数化方法，在木星-木卫一-木卫二与天王星-泰坦尼亚-欧伯隆系统的CCR4BP模型中计算了次级共振周期轨道（SPOs）及其分离子。
• 在木星-木卫一-木卫二CCR4BP模型（ε = 2.5265 × 10⁻⁵）中成功延拓了频率比ω/(2π) = 11/34、34/105、23/71、35/108、12/37、25/77、37/114和45/139的SPOs，其中由于共振重叠，不变环面已无法持续存在。
• 在两个系统中均检测到连续SPO分离子的交点，证实了在ω < 2.04047（木星系）及类似低频范围（天王星系）区域中环面破坏的动力学机制。
• 通过结合Floquet方向的参数化方法，实现了分离子的精确计算，成功在作用-角坐标系下可视化了非线性结构。
• 所有计算均在Julia中完成，使用OrdinaryDiffEq.jl、TaylorSeries.jl和TaylorIntegration.jl；数值积分采用DP8自适应步长方法；SPOs计算精度为10⁻⁷，步长Δε为5 × 10⁻⁷至10⁻⁶。