一句话总结

中国人民大学与字节跳动种子团队提出一种轻量级专家-路由器耦合（ERC）损失，通过使用扰动后的路由器嵌入作为代理令牌，强制对齐路由器决策与专家能力，借助双重激活约束确保每个专家专注于其分配的令牌，从而在计算效率上优于先前方法，并实现对参数量达150亿的MoE-LLM中专家专业化程度的细粒度追踪。

主要贡献

• 混合专家（MoE）模型存在路由器决策与专家能力之间耦合较弱的问题，导致令牌路由不理想且专业化受限，尽管具备效率优势，但整体性能仍受制约。
• 所提出的专家-路由器耦合（ERC）损失引入了一种轻量级、$n^2$n2复杂度的辅助损失，强制执行两个关键约束：每个专家对其自身代理令牌（由扰动后的路由器嵌入生成）的激活应强于对其他代理令牌的激活；同时，每个代理令牌应使其对应专家的激活最强，从而紧密耦合路由器表示与专家能力。
• 在30亿至150亿参数的MoE-LLM上进行大规模预训练（使用数万亿令牌）表明，ERC损失在保持极低训练开销的同时提升了下游性能，并支持在训练过程中对专家专业化程度进行定量追踪与灵活控制。

引言

作者针对混合专家（MoE）语言模型中的一个关键局限性展开研究：路由器决策与专家能力之间的耦合较弱，可能导致专家利用效率低下，进而影响模型性能。这种解耦常导致专业化程度不足以及推理阶段资源分配不均。为克服该问题，作者提出一种专家-路由器耦合（ERC）损失，在训练过程中紧密对齐路由器参数与其对应专家。ERC损失以极小的额外训练成本显著提升下游任务性能，并为专家专业化提供了更深入的洞察，为未来MoE模型研究提供了有力工具。

方法

作者提出一种新颖的辅助损失——专家-路由器耦合（ERC）损失，以解决MoE模型中缺乏显式约束来保证路由器决策与专家能力对齐的问题。ERC损失的核心是一个三步流程，作用于路由器的参数矩阵，将每一行视为代表一个被路由至特定专家的令牌簇的聚类中心。该框架由附图展示。

第一步是为每个专家生成一个扰动后的代理令牌。具体而言，每个路由器参数向量 $R[i]$R[i] 通过添加有界随机噪声 $\delta_i$δi​ 生成代理令牌 $\tilde{R}[i] = R[i] \odot \delta_i$R~[i]=R[i]⊙δi​。该噪声建模为乘性均匀分布，确保代理令牌能泛化至其对应专家所处理的令牌，同时保持在同一簇内。第二步将这 $n$n 个代理令牌分别输入所有 $n$n 个专家。对于输入 $\tilde{R}[i]$R~[i]，计算每个专家 $j$j 的中间激活范数，形成一个 $n \times n$n×n 矩阵 $M$M，其中 $M[i,j] = \| \tilde{R}[i] \cdot W_g^j \|$M[i,j]=∥R~[i]⋅Wgj​∥。该步骤设计为计算高效，仅需 $n^2$n2 次激活，与批量大小无关。

第三步即最终步骤，通过在矩阵 $M$M 上施加两个约束来实现专家-路由器耦合。对于所有 $i \neq j$i=j，损失惩罚专家 $j$j 对代理令牌 $i$i 的激活范数超过专家 $i$i 对其自身代理令牌激活范数的缩放版本的情况，反之亦然。形式化表达为 $M[i,j] < \alpha M[i,i]$M[i,j]<αM[i,i] 与 $M[j,i] < \alpha M[i,i]$M[j,i]<αM[i,i]，其中 $\alpha$α 为标量超参数。整体ERC损失为这些违规项正部分的均值，定义如下：

最小化该损失可确保每个专家对其自身代理令牌的激活最强（促进专家专业化），同时每个代理令牌能激发其对应专家的最强激活（确保精确的令牌路由）。ERC损失设计为轻量级，具有固定的计算成本 $2n^2Dd$2n2Dd FLOPs，且不引入超过基础MoE的激活密度，因此是一种实用且高效的增强方法。作者还证明，ERC损失可提供专家专业化的定量度量，因为超参数 $\alpha$α 直接控制专业化程度。

实验

• 使用ERC损失增强的MoE在多个基准测试中优于原始MoE，并缩小了与AoE的差距，在ARC-Challenge、CommonsenseQA、MMLU等任务上均取得显著且稳定的提升，30亿与150亿参数模型均表现出一致改进。
• 在30亿模型上，ERC损失的负载均衡能力与原始MoE相当（差异约10⁻⁵），并保持近乎相同的训练吞吐量与内存使用，而AoE的训练时间增加1.6倍，内存使用增加1.3倍，难以扩展。
• ERC损失引入的开销可忽略不计——在真实分布式训练中仅增加0.2–0.8%，源于其极低的FLOP成本（仅为基线前向传播的0.18–0.72%），理论分析与实测吞吐量均证实了这一点。
• ERC损失有效促进专家专业化，t-SNE可视化与定量指标均显示：专家参数聚类增强，且噪声水平 ε 与由 α 控制的专业化程度之间存在可测量的相关性。
• 消融研究证实，ERC损失中的随机噪声 δ 对泛化至关重要，该损失无法被对路由器或专家的独立约束（如路由器正交性）替代，即使路由器嵌入已接近正交，此类约束也仅带来有限提升。
• 最优专业化程度并非极端；当 α 过于严格时性能下降，表明专业化与协作之间存在权衡，最优 α 值依赖于模型规模（例如，n=64时 α=1，n=256时 α=0.5）。
• ERC损失在大规模模型上依然有效：在150亿参数模型（n=256，K=8）上，其在MMLU-Pro、AGI-Eval、MATH、GSM8K等挑战性基准上均实现性能提升，而AoE因成本过高无法训练。

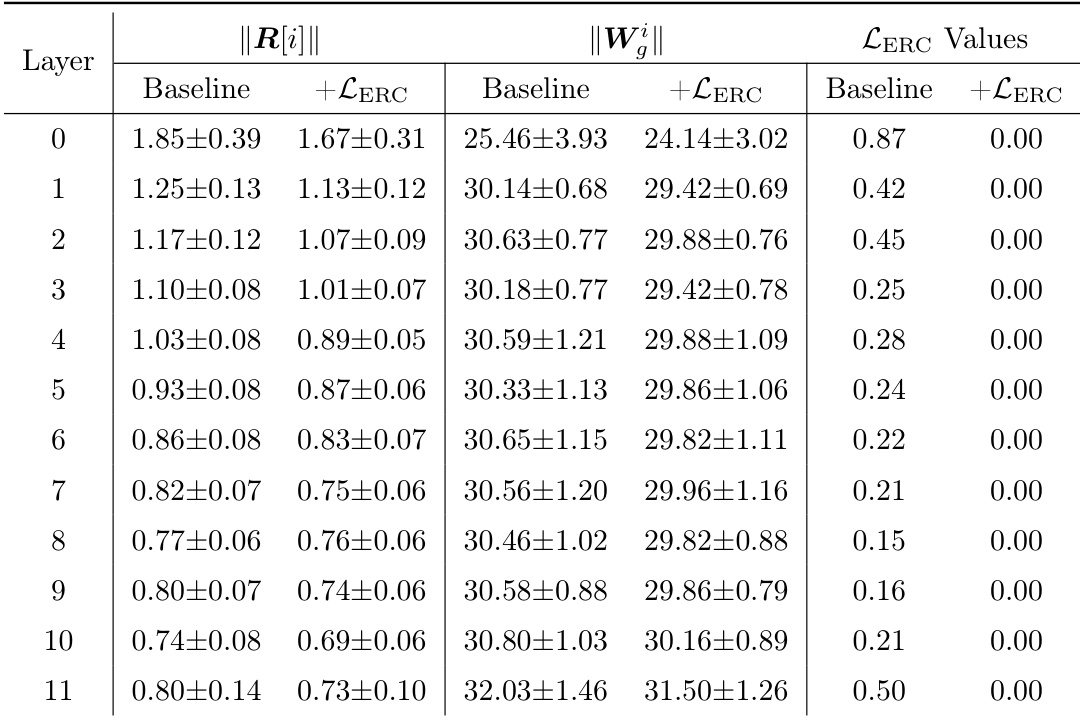
作者使用ERC损失强化MoE模型中路由器与专家之间的耦合，表格显示，该损失在所有层中均显著降低ERC损失值，应用后降至0.00。这表明模型能有效对齐路由器与专家参数，如+LERC列所示，ERC损失接近零，而基线值仍非零。

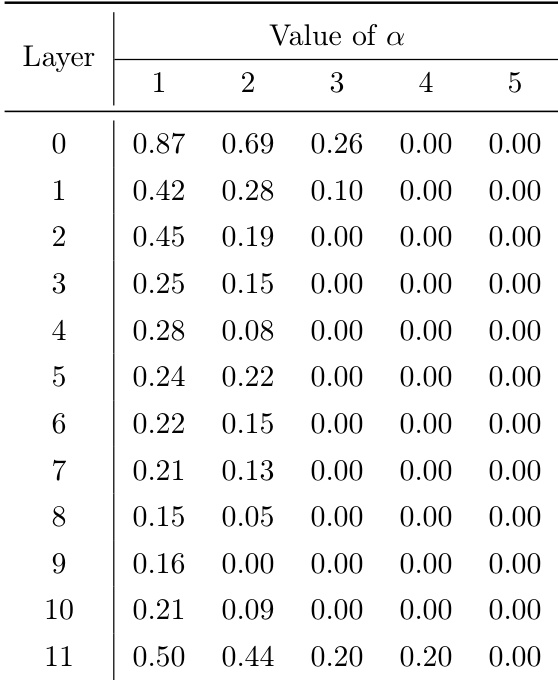
作者通过调节耦合强度参数 α 来研究专家专业化，表格显示，随着 α 增大，各层ERC损失下降，表明专业化程度降低。该趋势与分析一致：更高的 α 值削弱了耦合约束，导致专家趋于同质化，性能提升减弱。

作者利用ERC损失增强MoE模型中的专家-路由器耦合，结果在多个基准测试中均实现一致的性能提升。结果显示，加入ERC损失的MoE模型在准确率上优于原始MoE基线，30亿与150亿参数模型均取得增益，同时保持低计算开销与有效的负载均衡。