一句话总结

来自上海人工智能实验室、上海交通大学、北京大学等机构的研究人员提出了InternGeometry，这是一种达到奖牌水平的几何学大语言模型（LLM）智能体，通过符号引擎迭代生成并验证命题，在动态记忆机制引导下，结合复杂度提升强化学习（CBRL）进行训练，仅用极少数据便解决了50道IMO几何题中的44道，并在效率上超越AlphaGeometry 2。

主要贡献

• InternGeometry 通过实现大语言模型（LLM）与符号引擎之间的长视野交互，解决了人工智能驱动的几何问题求解中启发式能力弱的挑战。该模型迭代提出命题和辅助构造，形式化验证其正确性，并利用反馈指导后续步骤。
• 该方法引入了一种动态记忆机制，用于维护和压缩交互历史，使每个问题可支持超过200步的推理；同时采用“复杂度提升强化学习”（CBRL），这是一种课程学习策略，在训练过程中逐步增加问题难度，以提升收敛性和泛化能力。
• 在50道IMO几何题（2000–2024）上的评估显示，InternGeometry 解决了其中44道，超过金牌得主平均分（40.9），优于 AlphaGeometry2（42）和 SeedGeometry（43），且仅使用1.3万条训练样本——仅为 AlphaGeometry2 数据量的0.004%——同时还能生成人类解法中未曾出现的新型辅助构造。

引言

作者利用大语言模型（LLM）智能体应对国际数学奥林匹克（IMO）级别的几何问题，这一领域此前由依赖大规模合成数据集和广泛搜索的专家系统（如AlphaGeometry 2）主导。几何问题因其需要创造性地添加辅助构造以及构建长链条证明，难以通过标准启发式方法或短视野推理建模。以往基于LLM的方法在此领域表现不佳，通常局限于初级问题，或受限于与符号推理工具的弱集成。

为解决这些局限，作者提出了InternGeometry，这是一种通过与符号引擎进行迭代交互而实现奖牌水平性能的LLM智能体。该智能体以自然语言提出命题和辅助构造，进行形式化验证，并在数百步推理过程中根据反馈进行反思，由动态记忆机制在多轮交互中保留关键信息。这种长视野、试错式的推理方式模仿了人类专家的策略，能够发现非平凡的证明路径。

核心创新是“复杂度提升强化学习”（CBRL），这是一种课程学习框架，根据智能体当前能力，逐步提升合成训练问题的难度。这种分阶段方法确保了策略学习的稳定性与强泛化能力，使InternGeometry在仅使用1.3万条训练样本（仅为AlphaGeometry 2数据量的0.004%）的情况下，解决了50道IMO几何题中的44道，超过金牌得主平均分（40.9）。值得注意的是，该模型能生成人类解法中未见的新型辅助构造，展现出几何推理中的涌现创造力。

方法

作者采用一种紧密耦合的架构，包含一个交互式几何证明引擎和一个推理智能体，专为处理几何定理证明中的长视野、多步骤特性而设计。系统通过自然语言推理、形式化动作执行和环境反馈的迭代循环运行，并借助动态内存管理实现数百步的可扩展交互。

框架的核心是InternGeometry-DDAR引擎，它在开源系统Newclid基础上扩展，增强了全局几何约束满足、双点处理能力，并集成了“圆幂定理”和“梅涅劳斯定理”等高级定理。引擎在各步骤中维护状态，包括已构造的辅助点、已证明的命题和几何关系。它执行智能体发出的动作——如构造点、圆或线，或提出并验证命题——并返回结构化反馈，指示成功或失败。这些反馈对引导智能体下一步推理至关重要。

几何证明智能体记为 $\mathbb{G}$G，以逐步方式运行。在每一步 $t$t，给定问题 $X$X 和压缩后的历史 $\mathfrak{W}(H_{t-1})$W(Ht−1​)，智能体输出一对 $[P_t, A_t]$[Pt​,At​]，其中 $P_t$Pt​ 为自然语言的思维链，$A_t$At​ 为领域特定语言（DSL）中的形式化动作。动作 $A_t$At​ 由引擎 $\mathbb{E}$E 执行，返回观测值 $O_t$Ot​ 并更新其内部状态。交互历史随之扩展为 $H_t = H_{t-1} + [P_t, A_t, O_t]$Ht​=Ht−1​+[Pt​,At​,Ot​]，作为后续推理的基础。

为应对交互历史指数级增长的问题，作者引入记忆管理器 $\mathfrak{W}$W，在保留核心动作和关键反馈的同时压缩早期交互内容。这使得智能体能持续关注关键结果——例如某个辅助构造是否成功，或某个命题是否已被证明——而不会被冗长的历史上下文淹没。如框架图所示，压缩后的历史在每一步反馈给智能体，支持长视野规划并减少上下文低效问题。

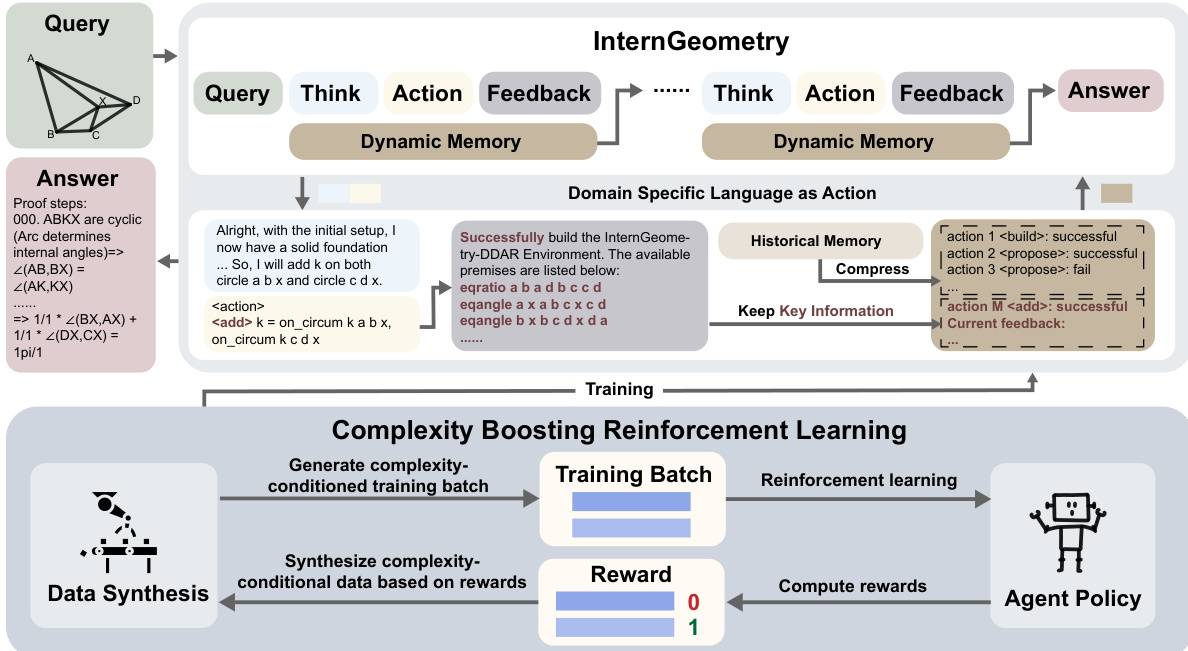
为缓解“动作崩溃”问题——即智能体陷入重复或退化输出模式——作者实现了一种先验引导的拒绝采样机制。在推理过程中，候选输出 $[\hat{P}_t, \hat{A}_t]$[P^t​,A^t​] 由基于规则的PassCheck策略评估，强制保证多样性、有效性和动作类型丰富性。违反这些约束的输出将被拒绝并重新采样，确保智能体在整个证明过程中保持有效探索。

训练分为两个阶段。首先，在合成数据集 $\mathcal{D} = \{(X^i, h^i, y^i)\}_{i=1}^N$D={(Xi,hi,yi)}i=1N​ 上进行监督微调，其中 $h^i = \mathfrak{W}(H^i)$hi=W(Hi)，$y^i = [P^i, A^i]$yi=[Pi,Ai]。目标是最小化智能体输出的负对数似然：

$$L_{\text{st}} = \frac{1}{N} \sum_{i=1}^{N} \left[ - \sum_{t=1}^{T} \log G_{\theta} \left( y_{t}^{i} \mid x^{i}, h_{t}^{i} \right) \right]$$Lst​=N1​i=1∑N​[−t=1∑T​logGθ​(yti​∣xi,hti​)]

该阶段培养了结构化思维和工具调用等基础行为。

第二阶段采用“复杂度提升强化学习”（CBRL），一种迭代的、课程驱动的强化学习循环。在每次迭代中，智能体尝试在由数据合成管道 $\mathfrak{X}(\kappa)$X(κ) 生成的、按复杂度条件采样的任务上进行证明，其中 $\kappa$κ 表示DDAR证明步数，作为问题难度的代理指标。智能体策略使用GRPO风格的目标更新，包含裁剪策略比和KL正则化：

$$\nabla J_{\text{rl}}(X, \theta) = \mathbb{E}_{y, h \sim G_{\theta}(\cdot \mid X)} \left[ \sum_{t=1}^{T} \min\left( \frac{G_{\theta}(y_t \mid X, h_t)}{G_{\theta_{\text{old}}}(y_t \mid X, h_t)}, \text{clip}\left( \frac{G_{\theta}(y_t \mid X, h_t)}{G_{\theta_{\text{old}}}(y_t \mid X, h_t)}, 1-\epsilon, 1+\epsilon \right) \right) A(X, y_t) \nabla \log G_{\theta}(y_t \mid X, h_t) \right] - \beta \nabla \mathbb{D}_{\text{KL}}(G_{\theta} \| G_{\text{ref}})$$∇Jrl​(X,θ)=Ey,h∼Gθ​(⋅∣X)​[t=1∑T​min(Gθold​​(yt​∣X,ht​)Gθ​(yt​∣X,ht​)​,clip(Gθold​​(yt​∣X,ht​)Gθ​(yt​∣X,ht​)​,1−ϵ,1+ϵ))A(X,yt​)∇logGθ​(yt​∣X,ht​)]−β∇DKL​(Gθ​∥Gref​)

奖励 $r$r 为二值：$r = r^o \wedge r^s$r=ro∧rs，其中 $r^o = 1$ro=1 表示证明完成，$r^s = 1$rs=1 表示该步动作有效（例如所提命题被证明，或辅助构造在最终证明中被成功使用）。优势函数 $A(X, y_t)$A(X,yt​) 在轨迹间归一化，以衡量相对步骤质量。

关键的是，CBRL 动态调整 $\kappa$κ，使平均奖励维持在0.5左右，从而最大化预期绝对优势，加速学习。其理论依据是：对于二值奖励，预期绝对优势 $2\sqrt{p(1-p)}$2p(1−p)​ 在 $p=0.5$p=0.5 时达到最大。数据合成管道通过采样原始结构、添加辅助构造，并选择仅在这些添加后才可证的结论，生成非平凡问题——确保训练数据既具挑战性又可解。

整个系统端到端训练，智能体策略通过与符号引擎的交互及奖励信号的反馈持续优化，使其通过迭代的、课程引导的探索掌握复杂的几何推理。

实验

InternGeometry 的推理方式和更大的模型确实增加了计算量。每个InternGeometry步骤都涉及自然语言推理，导致更多token和更高计算开销：在IMO-50上，每条轨迹平均输出token数为89.6K。InternGeometry模型（32B）也大于AlphaGeometry 2（3.3B）。由于AlphaGeometry 2的总成本未知，直接比较困难。但我们强调，更深层次推理和更大模型带来的额外计算不应被视为缺点，而应视为一种可行的新扩展维度——与训练数据规模和搜索解数量并列——这一维度比专家模型的图解方法更自然地契合基于LLM的路径。

InternGeometry作为LLM智能体，仅用1.3万训练样本便解决了50道IMO几何题中的44道，尽管数据量比AlphaGeometry 2和SeedGeometry低几个数量级，仍实现了超越。其Pass@256采样设置在远小于专家模型的训练数据集上取得该结果，而专家模型依赖数亿数据点。结果表明，当与定向数据合成和测试时扩展相结合时，基于LLM的智能体在专家级几何推理中具有高效性。

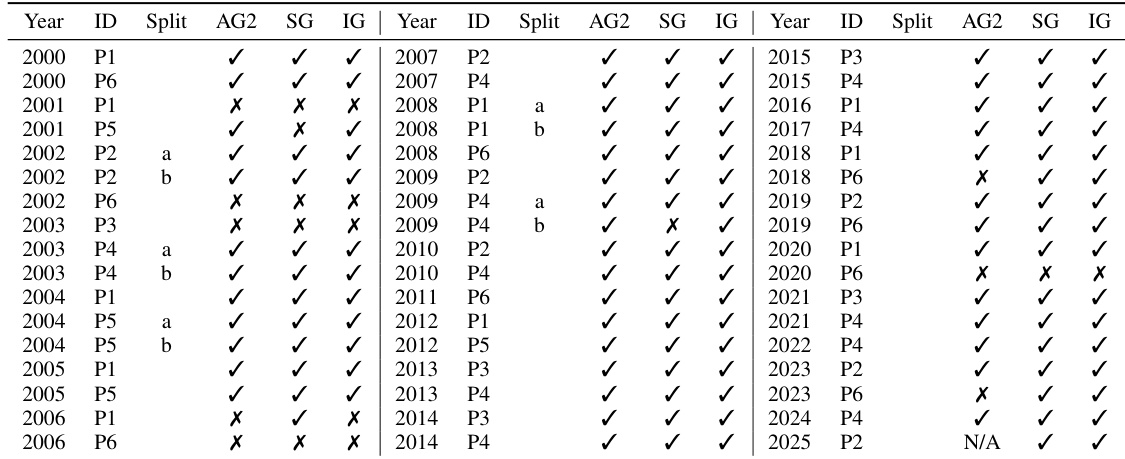
InternGeometry在50道IMO几何题中解决了44道，在此基准上优于AlphaGeometry 2和SeedGeometry。它还额外解决了此前两个模型均未解出的两道题——2018年第6题和2023年第6题——仅在三道题上失败，其中两道涉及当前系统范围之外的非几何计算。该模型以显著更少的训练数据和更高效的推理预算实现了这一成绩。

作者通过消融实验评估InternGeometry中各长视野智能体组件的贡献，结果显示移除“命题生成”、“慢思考”、“上下文压缩”或“拒绝采样”中的任一组件都会降低IMO 50上的性能。结果表明所有四个组件均至关重要：完整配置解决50题中的44道，而移除任一单个组件会使性能至少下降6题。“慢思考”和“上下文压缩”影响最大，各自贡献了超过10道额外解决的问题。

结果显示，使用CBRL训练的InternGeometry在IMO 50上达到44/50，显著优于仅监督微调的22/50基线。在强化学习阶段仅使用简单或仅使用困难数据时，性能分别降至29/50和24/50；而移除动态难度调度后性能降至38/50，验证了基于课程的强化学习的重要性。