摘要

来自莱斯大学、明尼苏达大学和约翰斯·霍普金斯大学的研究人员提出 DTS，这是一种与模型无关的解码框架，通过选择性地探索高熵决策点并优先选择较短的推理路径，减少大型推理模型中的“过度思考”现象。DTS 在无需重新训练的情况下，将准确率最高提升 8%，并将推理长度缩短 23%，从而在复杂任务上实现更高效、更准确的 AI 推理。

主要贡献

• DTS 引入了一种无需训练、与模型无关的解码框架，通过在推理过程中选择性地探索高熵决策点，减少大型推理模型（LRM）中的过度思考。
• 它利用并行自回归生成构建紧凑的解码树，并通过早停机制识别最短且完整准确的推理路径。
• 实验表明，DTS 在 AIME2024 和 AIME2025 基准测试中，准确率最高提升 8%，平均推理长度减少 23%，重复频率降低 12%。

引言

大型推理模型（LRMs）通过生成逐步的思维链（CoT）推理，在复杂任务上表现出色，但常常出现“过度思考”现象——产生冗长且重复的推理路径，增加推理成本并损害准确性。以往的研究尝试通过基于训练的方法（如在压缩数据或长度惩罚数据上进行监督微调或强化学习）或自适应剪枝机制来解决这一问题。然而，这些方法需要额外的标注数据和训练过程，限制了可扩展性，而无需训练的方法往往缺乏一致的性能提升。

作者利用了一个观察结果：较短的推理路径在经验上更准确。在自回归生成过程中，推理空间形成一棵树结构，其中最优路径较短，但却埋藏在指数级增长的搜索空间中。为了在无需训练的情况下高效逼近最佳路径，作者提出了 DTS（Decoding Tree Sketching，解码树草图），这是一种与模型无关的解码框架，能够在推理时动态构建紧凑的推理树。

• 使用下一个词元的熵值，仅在高不确定性词元处选择性地分支，降低搜索复杂度。
• 应用早停机制，返回最先完成的最短推理路径，与观察到的准确率与长度之间的负相关性保持一致。
• 完全在解码阶段运行，并利用 GPU 并行性，实现无需训练、即插即用的跨模型部署。

方法

作者采用一种名为解码树草图（DTS）的新颖解码策略，以高效识别大型推理模型（LRMs）中最短的推理路径，利用推理长度与准确率之间的负相关性。DTS 并不穷举所有可能推理序列的指数级增长空间，而是构建一棵剪枝后的解码树，仅在高不确定性词元处选择性地扩展分支，从而在保持计算可行性的前提下逼近最优短路径。

DTS 的核心机制依赖于一个自适应分支函数 $F(x, \xi)$F(x,ξ)，该函数决定在每个解码步骤是生成单个词元还是生成多个分支。该决策由下一个词元分布 $P(v) = f(x, \xi)$P(v)=f(x,ξ) 的熵 $H(v)$H(v) 控制，其中 $f$f 表示 LRM。当 $H(v) \geq \tau$H(v)≥τ 时，表示不确定性较高，DTS 选择概率最高的前 $K$K 个词元以启动新分支；否则，仅采样一个词元。形式化表示如下：

$$F(x, \xi) = \begin{cases} \{ v_1, \dots, v_K \mid p_{v_1}, \dots, p_{v_K} \geq \tilde{p}_K \} & \text{if } H(v) \geq \tau, \\ \{ v_1 \},\ v_1 \sim P(v) & \text{if } H(v) < \tau, \end{cases}$$F(x,ξ)={{v1​,…,vK​∣pv1​​,…,pvK​​≥p~​K​}{v1​}, v1​∼P(v)​if H(v)≥τ,if H(v)<τ,​

其中 $\tilde{p}_K$p~​K​ 是 $P(v)$P(v) 中第 $K$K 大的概率值。这种基于熵的门控机制使 DTS 能够将计算资源集中在模型不确定的推理区域，而在确定性高的区域则以确定性方式推进。

如下图所示，解码树以广度优先的方式增长，每个节点代表一个词元，边表示转移关系。仅在步骤 $t_1$t1​ 和 $t_2$t2​ 处发生分支，此时熵值超过阈值 $\tau$τ，并选择概率最高的两个词元进行扩展。低熵步骤则线性推进，保持高效性。

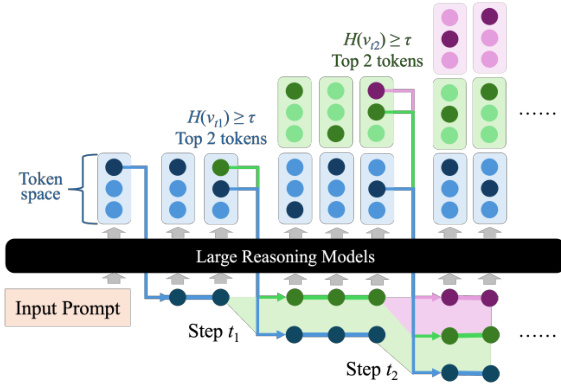
在每个时间步 $t$t，DTS 维护一组活跃的推理序列 $\mathcal{T}_t$Tt​，初始为 $\mathcal{T}_0 = \varnothing$T0​=∅。对于每个序列 $\xi \in \mathcal{T}_t$ξ∈Tt​，模型应用 $F(x, \xi)$F(x,ξ) 生成下一个词元，并将其附加以形成新序列。然后更新集合：

$$\mathcal{T}_{t+1} = \{ \xi \oplus v_i \mid v_i \in F(x, \xi),\ \xi \in \mathcal{T}_t \}.$$Tt+1​={ξ⊕vi​∣vi​∈F(x,ξ), ξ∈Tt​}.

该过程迭代进行，所有分支并行生成，以利用 GPU 加速，确保可扩展性。

一旦任意分支生成结束词元 $\langle e \rangle$⟨e⟩，即触发早停，遵循“较短推理路径准确率更高”的原则。形式上，若 $\bigvee_{\xi \in \mathcal{T}_t} \mathbb{1}[\langle e \rangle \in \xi]$⋁ξ∈Tt​​1[⟨e⟩∈ξ] 成立，则 DTS 在步骤 $t$t 停止，并将第一个完成的序列作为最终输出。

下图展示了一个示例：DTS 处理提示“一个长为 12、宽为 9 的矩形面积是多少？”在步骤 $t_1$t1​ 和 $t_2$t2​ 发生分支，生成多条推理路径。紫色分支最先终止，得出正确答案“area= 12×9=108”，并作为最终输出返回。

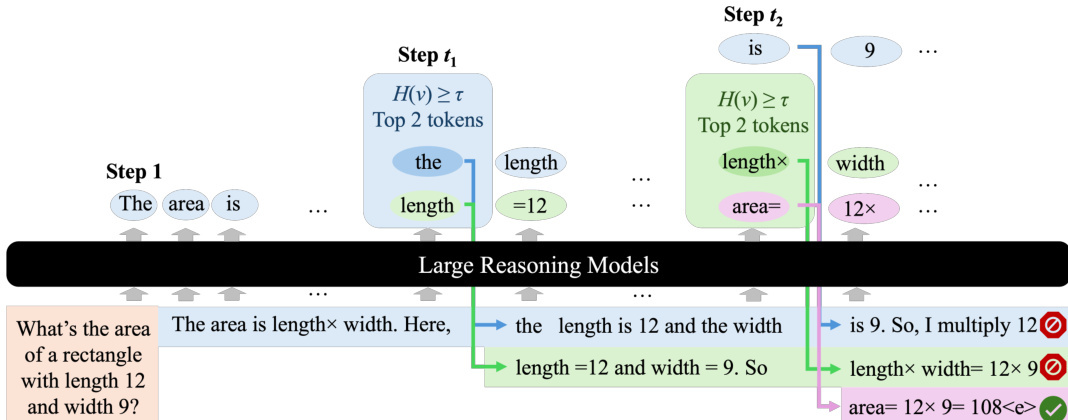
该算法在草图树上执行广度优先搜索，确保识别出最短的有效推理路径。所有活跃分支并行扩展，实现高效且可扩展的推理，同时不牺牲推理输出的质量。

实验

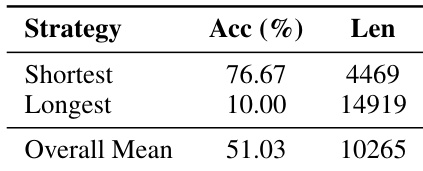
作者对每个 AIME24 问题使用 100 次随机解码来评估推理轨迹，发现选择最短响应的准确率为 76.67%，且使用的词元数显著少于最长或平均响应。结果表明响应长度与准确率之间存在强负相关性，说明冗长的推理会降低性能。这支持了 DTS 的设计动机，即优先选择更短、更高效的推理路径，以提升准确率和效率。

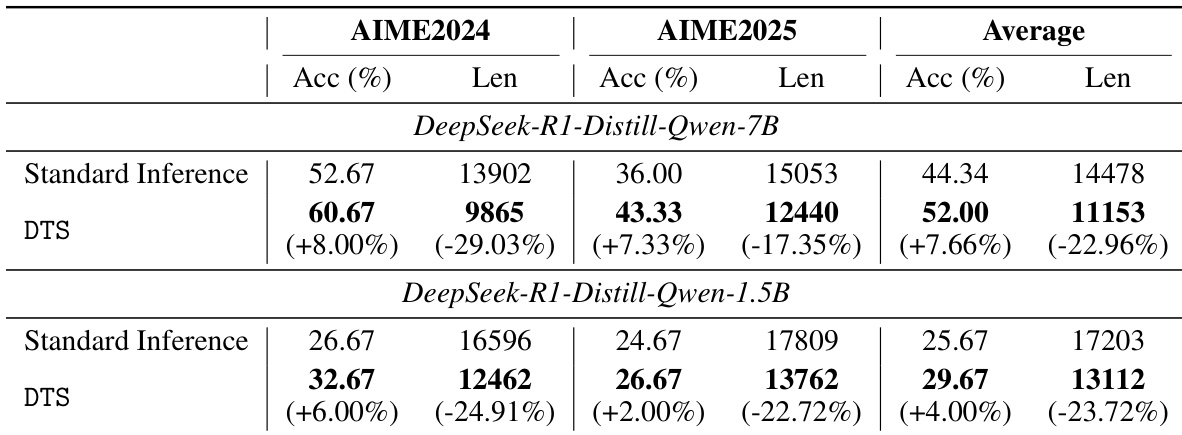
作者使用 DTS 框架提升 DeepSeek-R1-Distill-Qwen 模型在 AIME2024 和 AIME2025 上的推理性能与效率。结果表明，与标准推理相比，DTS 始终将准确率提高 4% 至 8%，同时将响应长度减少 17% 至 29%，其中 7B 模型平均准确率提升 7.66%，长度减少 22.96%。这些改进在不同模型规模和数据集上均成立，证明 DTS 在无需训练的情况下有效平衡了性能与效率。

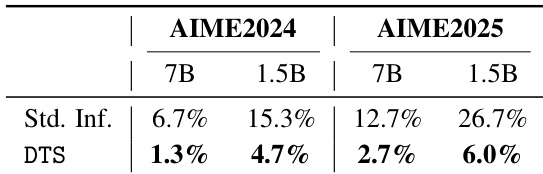
作者使用 DTS 减少推理轨迹中的无限重复现象，结果显示其在 7B 和 1.5B 模型上均降低了 AIME2024 和 AIME2025 基准测试中的重复率。结果表明，DTS 将 7B 模型在 AIME2024 上的重复率从 6.7% 降至 1.3%，将 1.5B 模型在 AIME2025 上的重复率从 26.7% 降至 6.0%。这证实 DTS 通过偏好更短且已完成的推理轨迹，有效剪除了重复路径。