一句话总结

来自 DeepSeek-AI 的作者提出了 DeepSeek-Prover-V2，这是一个 671B 参数的开源模型，用于 Lean 4 中的形式化定理证明，通过利用 DeepSeek-V3 的递归流水线整合非形式化与形式化推理；其在 MiniF2F-test 上实现了 88.9% 的通过率，并解决了 15 道 AIME 问题中的 6 道，显著缩小了自然语言与形式化数学推理之间的差距。

主要贡献

• 本文解决了大型语言模型中非形式化数学推理与 Lean 4 形式化定理证明严格要求之间的鸿沟问题，提出了一种基于 DeepSeek-V3 的递归定理证明流水线，能够生成自然语言证明草图和形式化子目标，从而构建统一的非形式化与形式化推理框架。

• 所提出的 DeepSeek-Prover-V2-671B 模型通过冷启动训练流程进行训练，该流程结合了 DeepSeek-V3 的思维链推理与分解子目标的形式化验证证明，随后进行强化学习，最终在 MiniF2F-test 上达到 88.9% 的通过率（Pass@8192），并在 PutnamBench 上解决了 47 个问题，性能达到当前最先进水平。

• 作者提出了 ProverBench，一个包含 325 个形式化问题的新基准，其中包括 15 道来自 AIME 竞赛（2024–2025）的问题，DeepSeek-Prover-V2-671B 成功解决了其中 6 道，显著缩小了大语言模型在形式化与非形式化数学推理之间的差距。

引言

作者致力于解决大型语言模型（LLMs）中非形式化数学推理与 Lean 等系统所要求的形式化定理证明语法严谨性之间的鸿沟。尽管 LLMs 在自然语言思维链推理方面表现出色，但其基于启发式的近似风格缺乏形式验证所需的精确性，后者要求每一步都必须明确证明。先前的方法尝试通过证明草图引导形式化证明构建，但面临训练信号稀疏和证明搜索效率低下的问题。为克服这些限制，作者提出了 DeepSeek-Prover-V2，采用两阶段流水线：首先，一个大型通用模型（DeepSeek-V3）生成高层证明草图，并递归地将复杂定理分解为 Lean 中形式化的子目标，中间步骤以 sorry 占位符保留；其次，一个小型 7B 证明模型递归解决这些子目标，实现高效的证明搜索。作者进一步通过构建从子目标衍生的难度递增的课程化猜想，生成密集且高质量的训练数据。该冷启动数据随后通过强化学习进行优化，显著提升了模型解决形式化证明的能力。最终的 DeepSeek-Prover-V2-671B 在 MiniF2F、ProofNet 和 PutnamBench 等基准上均达到最先进性能，并成功解决具有挑战性的 AIME 问题，展现出强大的泛化与推理能力。

数据集

• 数据集名为 ProverBench，包含 325 个形式化数学问题，结合了 15 道来自 AIME 24&25 竞赛的问题和 310 道从精选高中及本科教材中提取的问题。
• AIME 子集仅包含数论与代数问题，旨在避免几何、组合与计数问题（这些在 Lean 中表示复杂），从而获得 15 个清晰、竞赛级别的形式化问题。
• 教材子集涵盖广泛的数学领域，包括数论、代数、线性代数、抽象代数、微积分、实与复分析、泛函分析以及概率，覆盖高中竞赛与本科水平内容。
• 该数据集旨在支持非形式化推理（如 AIME）与形式化证明生成（如教材问题）的评估，实现不同推理模式下模型性能的直接比较。
• 作者使用 ProverBench 在形式化证明生成设置中评估 DeepSeek-Prover-V2-671B，模型需从给定的正确答案构建有效的 Lean 4 证明。
• 对于 AIME 问题，采用 16 次采样响应的多数投票机制进行“找答案”任务评估；对于教材问题，则评估其生成正确形式化证明的能力。
• 数据集已处理以确保与 Lean 4.9.0 兼容，评估过程中排除了有问题或表述错误的命题。
• 作者还利用 Dong 和 Ma（2025）发布的公开合成数据集进行监督微调，该数据集包含 ProofNet 有效问题的变体，而原始 ProofNet-test 划分则专用于最终模型评估。
• 模型训练使用多种数据源的混合，包括高中水平问题和大学水平形式化内容，从而实现对高级数学领域的强泛化能力。
• 训练过程中引入思维链（CoT）推理，显著提升了在 ProofNet-test 和 PutnamBench 上的通过率，相比非 CoT 设置表现更优。
• 采用裁剪策略排除与 Lean 4.9.0 不兼容的问题，尤其在 PutnamBench 中，因初始评估发现两个问题表述错误，已被移除。
• 每个问题的元数据包括主题分类、难度等级和来源（AIME 或教材），支持对模型在不同领域与推理风格下的性能进行详细分析。

方法

DeepSeek-Prover-V2 的模型架构围绕一个两阶段训练流水线设计，融合非形式化数学推理与形式化证明构建，通过递归定理证明框架合成高质量训练数据。整体方法利用 DeepSeek-V3 作为高层推理引擎，将复杂问题分解为可管理的子目标，再由小型 7B 证明模型递归解决。该分解过程被形式化为结构化思维链，其中 DeepSeek-V3 的中间推理步骤与 7B 模型生成的形式化证明相结合，形成连贯统一的数据集。由此产生的冷启动数据（包含非形式化推理与形式化证明步骤）成为训练更大规模 DeepSeek-Prover-V2-671B 模型的基础。

训练过程始于冷启动阶段，通过递归分解挑战性问题生成合成数据。作者使用 DeepSeek-V3 将问题分解为一系列子目标，随后利用 7B 证明模型合成这些子目标的形式化证明。已解决子目标的证明被组合成原始问题的完整形式化证明。该完整证明被附加至 DeepSeek-V3 的思维链推理中，后者描述了引理分解过程，从而构建一个融合非形式化与形式化推理的统一数据集。该合成数据用于初始化模型，为后续优化提供强大起点。

两阶段训练流水线包括监督微调（SFT）阶段和强化学习（RL）阶段。第一阶段在课程学习框架内采用专家迭代训练一个非思维链（non-CoT）证明模型。该模型优化为快速生成形式化 Lean 代码，无需显式中间推理步骤，从而加速迭代训练与数据收集过程。该阶段的训练语料由专家迭代收集的非 CoT 数据（生成简洁 Lean 代码）和从 DeepSeek-V3 推理模式合成的冷启动 CoT 数据组成。非 CoT 数据强调形式化验证能力，而 CoT 数据则显式建模将数学直觉转化为形式化证明结构的认知过程。

第二阶段通过强化学习阶段增强模型在非形式化推理与形式化证明构建之间的桥梁能力。作者采用组相对策略优化（GRPO）作为训练算法，通过为每个定理提示采样一组候选证明，并基于其相对奖励优化策略，从而无需独立的评判模型。训练使用二元奖励机制，每个生成的 Lean 证明若经验证正确则获得 1 分，否则为 0 分。为确保有效学习，训练提示仅包含对监督微调模型而言足够具有挑战性但又可解的问题。每次迭代采样 256 个不同问题，每个定理生成 32 个候选证明，最大序列长度为 32,768 个 token。该过程使模型能够不断优化其推理与证明构建能力，显著提升形式化定理证明性能。

实验

• 在 CombiBench 上，DeepSeek-Prover-V2-671B 在有解设置下解决了 77 个问题中的 10 个，展示了对组合问题的泛化能力，尽管训练重点在数论与代数；模型还表现出检测并适应错误表述问题的能力。
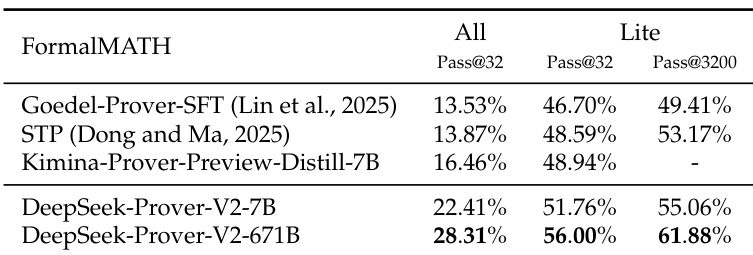
• 在 FormalMATH-Lite 上，DeepSeek-Prover-V2-671B 在 32 个样本下取得 56.00% 的成功率，提升至 3200 个样本时达到 61.88%，优于 Goedel-Prover-SFT、STP 和 Kimina-Prover-Preview-Distill-7B 等先前模型；在完整 FormalMATH-All 数据集上，解决了 28.31% 的问题。
• 在 ProverBench 上，DeepSeek-Prover-V2-671B 在完整集（325 个问题）和 AIME 24&25 子集上均取得优异表现，展现出与最先进证明器相当的竞争力。

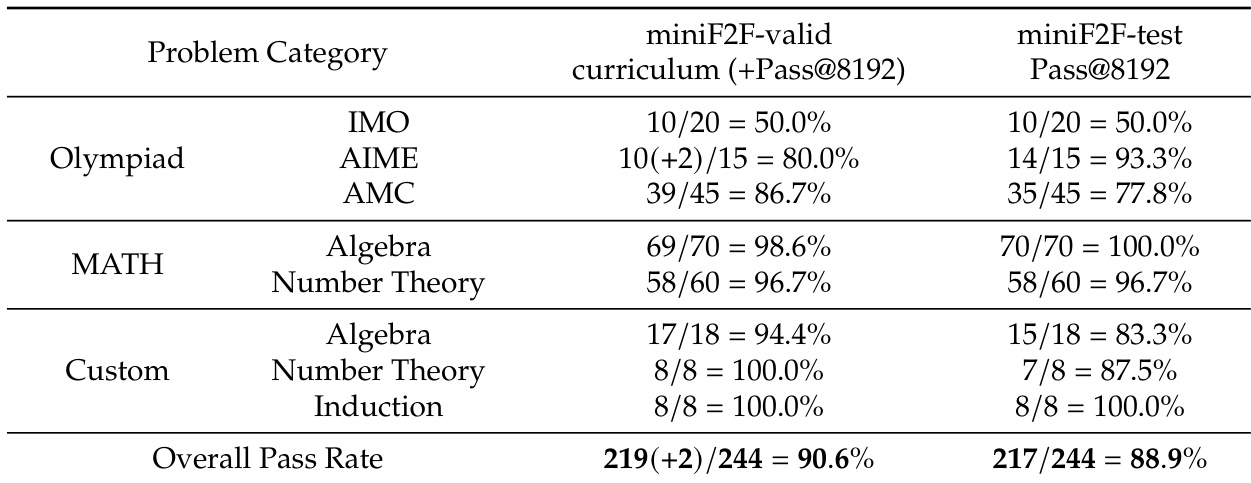
作者使用 miniF2F 基准评估 DeepSeek-Prover-V2 在形式化定理证明任务上的表现，报告了不同问题类别和数据集上的通过率。结果显示，该模型在 miniF2F-valid 课程上达到 90.6% 的高总体通过率，在 miniF2F-test 集上达到 88.9%，尤其在代数与数论问题上表现突出。

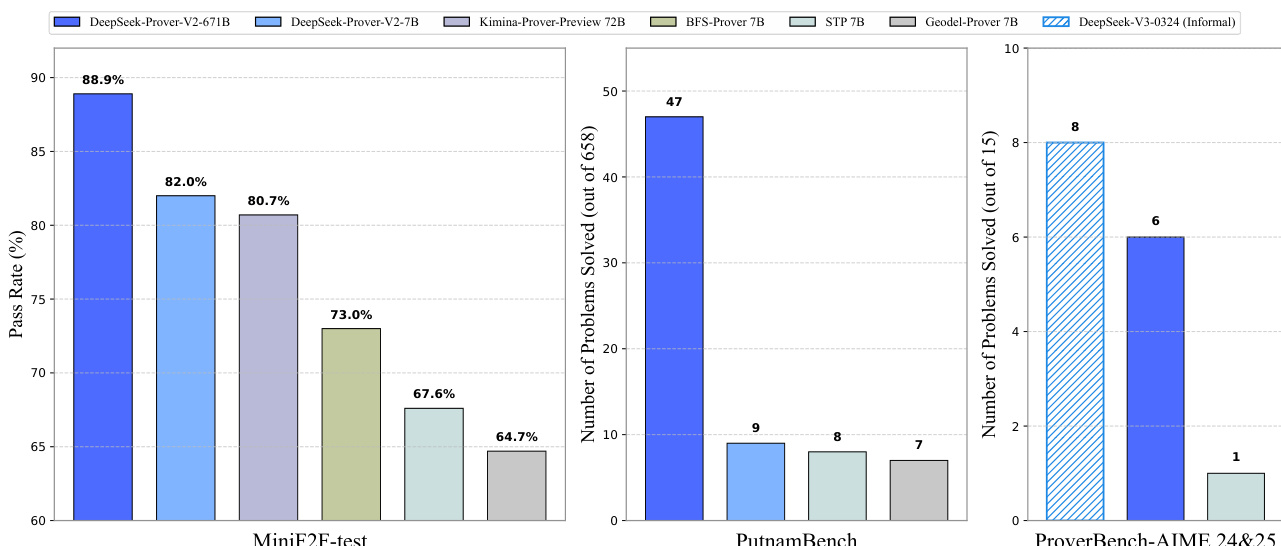
作者使用 DeepSeek-Prover-V2-671B 评估在 MiniF2F-test、PutnamBench 和 ProverBench-AIME 24&25 上的表现，分别取得 88.9%、82.0% 和 80.7% 的通过率，在 MiniF2F-test 上解决了 47/658 个问题，在 PutnamBench 上解决了 47 个问题，在 ProverBench-AIME 24&25 上解决了 8/15 个问题。结果表明，DeepSeek-Prover-V2-671B 在所有基准上均优于其他模型，尤其在 MiniF2F-test 上与第二名模型相比领先 6.9 个百分点。

结果显示，DeepSeek-Prover-V2-671B 在 FormalMATH-Lite 上表现最佳，使用 3200 个样本时解决了 61.88% 的问题，优于所有基线模型。在完整 FormalMATH 数据集上，使用 32 个样本解决了 28.31% 的问题，相比其他模型展现出更强的有效性。

作者使用提供的表格比较 DeepSeek-Prover-V2-7B 与 DeepSeek-Prover-V2-671B 在非 CoT 与 CoT 生成模式下的性能，输出 token 数分别设为 7B 与 671B。结果显示，CoT 模式显著提升了两种模型的性能，其中 671B 模型在 CoT 设置下达到最高分 6751.9。

结果显示，DeepSeek-Prover-V2 在多个基准上均表现强劲，671B 模型在 ProofNet-test 与 PutnamBench 上均优于其他方法。DeepSeek-Prover-V2 的 CoT 版本显著提升结果，尤其在 PutnamBench 上，671B 模型达到 47/658，充分证明了思维链推理的有效性。