一句话总结

作者Moshkov、Hanley、Sorokin、Toshniwal、Henkel、Schifferer、Du和Gitman提出了一种前沿的数学推理框架，该框架整合了包含540K题目的OpenMathReasoning数据集与三项核心创新：用于在长链式思维（CoT）中集成代码执行的迭代训练工具集成推理（TIR）方法、一种新颖的生成式解法选择（GenSelect）机制以从多个候选解法中识别最优解，以及一种控制代码执行次数的流水线。其OpenMath-Nemotron模型在AIMO-2上取得顶尖表现，成功解决50题中的34题，并以宽松许可协议发布，推动开源数学AI的发展。

主要贡献

• 我们提出了OpenMathReasoning，一个大规模数据集，包含540K个独特高质量数学问题（包括奥数级别挑战）和320万条长篇推理解答，支持具备强大数学推理能力的开放权重模型的有效蒸馏与训练。

• 我们开发了一种新颖的迭代训练流水线，通过工具集成推理（TIR）将代码执行整合进长推理模型，结合指令微调模型生成与激进质量过滤及可控执行次数，生成了170万条高质量解答。

• 我们提出了生成式解法选择（GenSelect），一种训练模型对多个候选解法进行排序并选择最优解的方法，在数学推理基准测试中显著优于多数投票法，实现了更高的pass@k性能。

引言

作者针对构建高精度数学推理模型以应对复杂奥数级问题的挑战展开研究，传统链式思维方法常因推理深度不足和缺乏可执行验证而失效。先前方法在训练数据规模有限、代码执行与推理流程整合不佳，以及依赖简单解法聚合（如多数投票）方面存在局限，导致性能远低于理论上限。为克服这些限制，作者提出三项关键创新：首先，构建了包含54万道题目的OpenMathReasoning数据集，配有320万条长篇推理解答，支持推理模式的稳健蒸馏；其次，开发了一种新颖的迭代训练流水线，用于训练模型整合代码执行（工具集成推理），通过质量过滤优化170万条高保真解答，并实现对执行次数的高效控制；第三，提出生成式解法选择（GenSelect），训练模型从多个候选解法中排序并选择最优解，性能超越多数投票。这些组件整合为一系列开放权重模型（15亿至320亿参数），支持CoT、TIR和GenSelect推理，在AIMO-2上达到最先进水平，获胜提交解决了50题中的34题。完整数据集、代码和模型均以宽松许可协议发布，以推动开放研究。

数据集

• 数据集由来自“问题解决的艺术”（AoPS）社区论坛的数学问题构成，排除“中学数学”类别，因其内容过于基础。
• 主要训练数据源自AoPS论坛讨论，整个处理流程采用Qwen2.5-32B-Instruct进行系统化处理。
• 问题提取步骤识别并分离出单个问题，处理包含多个或无问题的情况。
• 每道问题被分类为：证明类、选择题、二元（是/否）或无效类。选择题、二元题和无效题被移除。
• 证明类问题被转换为基于答案的问题，以匹配模型的预期输出格式。
• 对非证明类问题，最终答案通过LLM辅助解析从论坛讨论中提取。
• 通过基准去污染步骤移除与现有数学基准高度相似的问题，使用基于LLM的比对确保数据新鲜度。
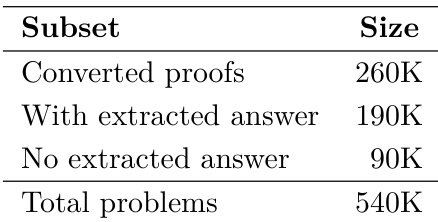
• 最终训练数据集由高质量、非证明类、单答案问题构成，具体规模与组成详见表1和表2。
• 构建了一个专用验证集Comp-Math-24-25，包含2024年和2025年美国邀请数学考试（AIME）及哈佛-麻省理工数学竞赛（HMMT）中的题目。
• 验证集包含256道题，选题标准与AIMO-2竞赛一致，涵盖相似主题与难度层级，排除证明类或部分得分题。
• 训练中使用多种题型混合，模型在清洗后的AoPS衍生问题上训练，并在Comp-Math-24-25基准上评估。
• 对于链式思维（CoT）解法，生成1.5万样本作为阶段0的TIR数据，代码执行经过筛选，仅保留包含新颖且重要代码块的解法。
• 代码块筛选基于两个标准：是否执行新颖计算或仅验证先前步骤，以及是否对解法有显著贡献。
• 丢弃最终答案错误、无代码执行或代码块超过两个的解法。
• 预处理阶段统一代码块分隔符：将Markdown风格的"python" and ""标签替换为"<tool_call>"和"</tool_call>"，以确保可靠提取。
• 为提升摘要质量，将DeepSeek-R1等推理模型的原生摘要替换为由Qwen2.5-32B-Instruct生成的新摘要。
• 每个解法生成四个候选摘要，长度上限2048 token，仅保留与原始解法答案一致的摘要，选取最长有效摘要。
• 此摘要重写过程应用于整个OpenMathReasoning数据集，以确保推理过程中摘要的一致性与信息量。

方法

作者开发了一种多阶段流水线，用于训练能够生成高质量工具集成推理（TIR）解法的模型，该解法结合自然语言推理与可执行Python代码。整体框架从问题输入开始，生成多个解法摘要。这些摘要被分类为正确与错误实例，构成生成式解法选择（GenSelect）过程的基础。GenSelect流水线旨在训练模型从一组候选摘要中选择最具潜力的解法，从而在性能上超越简单的多数投票。

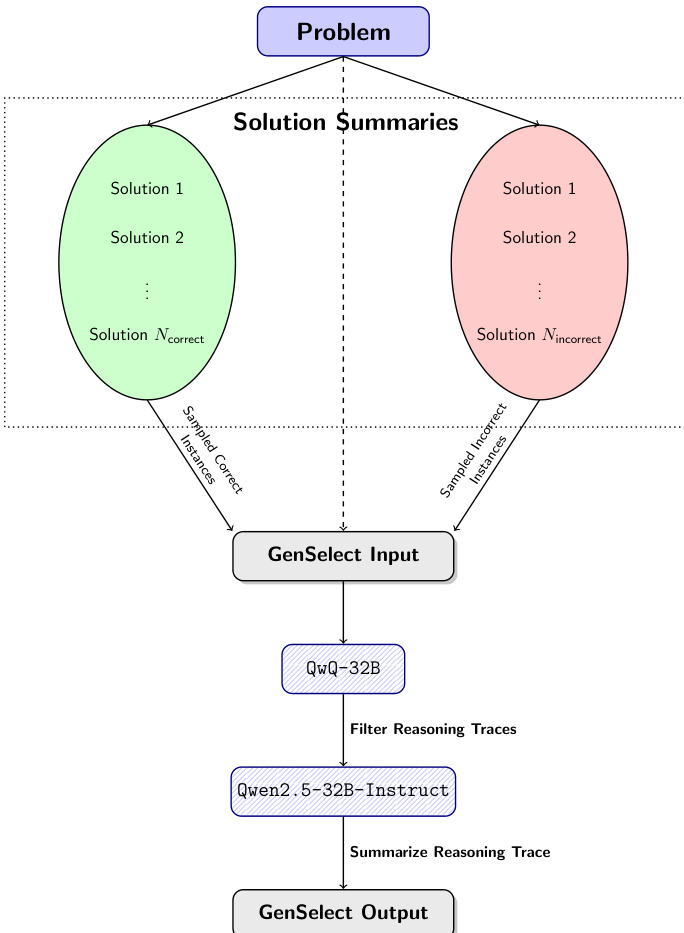
如图所示，流程从一个问题开始，生成一组解法摘要。这些摘要随后分为两组：采样的正确实例与采样的错误实例。两组均输入GenSelect输入模块，作为训练基础。使用QwQ-32B模型为这些输入生成推理轨迹，随后通过过滤保留高质量推理。过滤后的轨迹传递给Qwen2.5-32B-Instruct模型，将其总结为最终的GenSelect输出。该流水线使模型能够学习比较并从多个候选解法中选择最具潜力的解法，利用自然语言推理完成选择。作者发现，相比孤立判断每个解法，此方法显著提升性能，因为它允许模型对不同解法路径的相对质量进行推理。

实验

• 使用DeepSeek-R1和QwQ-32B生成120万条CoT解法，温度0.7，top-p 0.95，token上限16384；通过Qwen2.5-32B-Instruct判断保留仅达到预期答案的解法，真实答案基于候选解法中的多数答案得出。
• 通过监督微调在550万样本（320万CoT、170万TIR、56.6万GenSelect）上训练OpenMath-Nemotron系列（15亿至320亿参数），采用RoPE扩展至50万上下文长度；在CoT准确率上取得显著提升，TIR性能保持稳定。
• 应用GenSelect，使用摘要化推理轨迹（上限2048 token）以降低推理成本；与完整轨迹相比，准确率下降1–2%，但实现高度可并行化的预填充和高效推理。
• 在Kaggle AIMO-2提交中，通过线性组合CoT与TIR检查点；使用推测解码（ReDrafter，3 token提案，65%接受率）与时间缓冲策略满足5小时限制，私有排行榜上实现34道正确解。
• 在Comp-Math-24-25基准上，OpenMath-Nemotron-14B（Kaggle）达到pass@1（maj@64）为78.4%（85.2%），平均生成长度比预期长10%，尽管本地性能强劲，但导致推理效率低下。

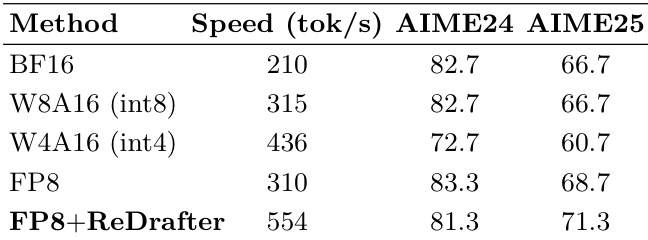
结果表明，FP8+ReDrafter方法在554 tok/s下实现最高速度，同时在AIME24和AIME25基准上保持竞争力，推理效率优于其他方法。

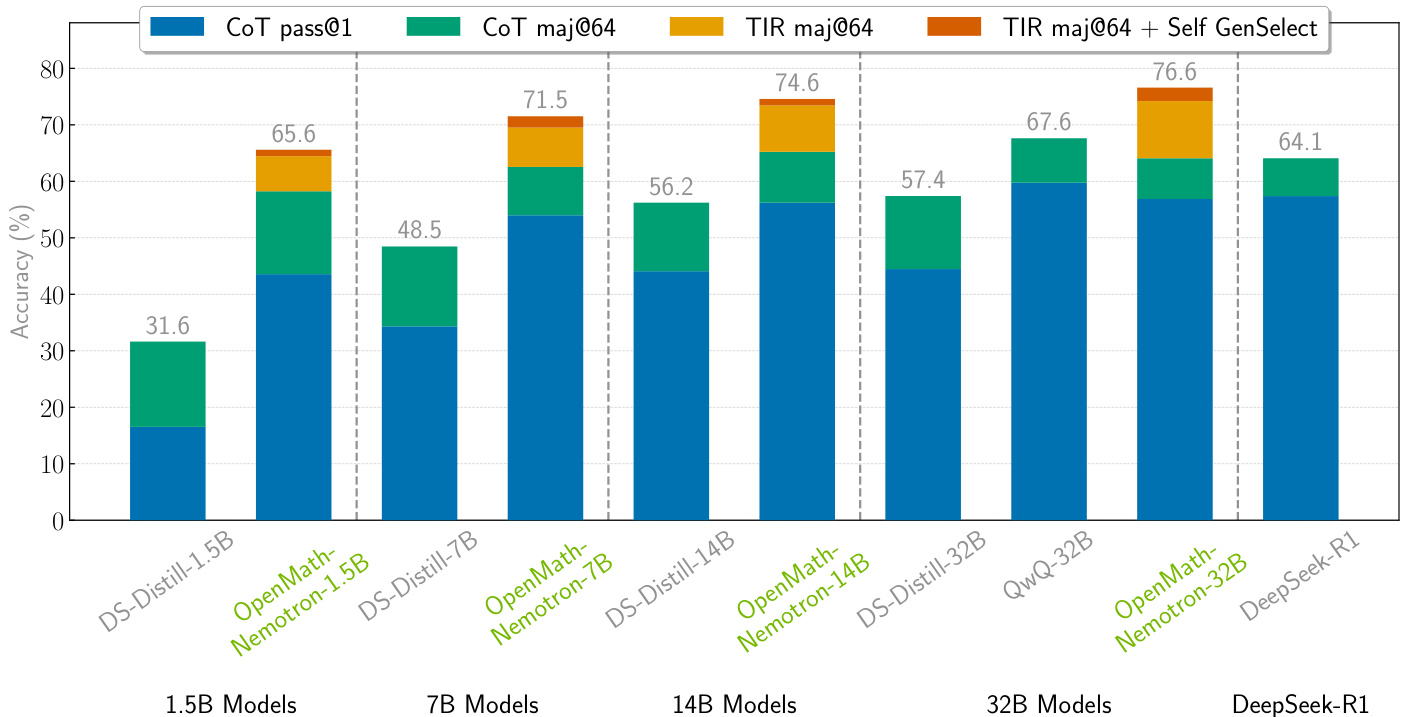
作者对比了多种模型在数学推理任务上的表现，评估了CoT与TIR生成方法。结果显示，OpenMath-Nemotron-32B模型在TIR maj@64 + Self GenSelect设置下达到最高准确率76.6%，显著优于较小模型及其他基线。

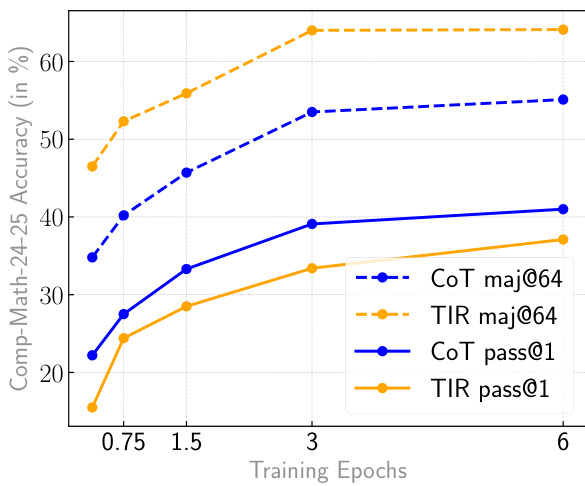
结果显示，所有训练周期中，CoT模型的准确率均高于TIR模型，CoT maj@64与CoT pass@1始终优于其TIR对应项。两种模型的准确率均随训练周期增加而提升，但CoT模型在多数投票设置中表现出更显著的改进。

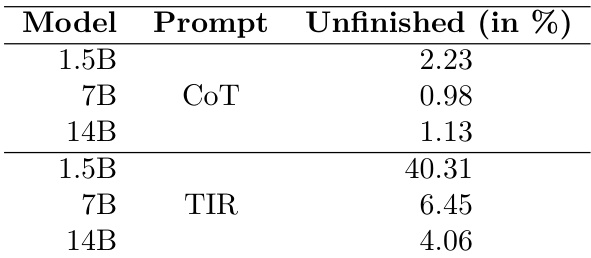
结果显示，TIR提示在所有模型规模下均导致未完成解法的比例显著高于CoT提示，其中15亿参数模型差异最为明显。作者推测，较小模型在有效使用工具方面一致性较差，这导致在使用TIR提示时未完成解法的比例更高。

作者展示了包含54万道数学问题的数据集，分为三个子集：26万道已转换的证明题、19万道提取出答案的题，以及9万道未提取答案的题。该分布反映了其数据集构建过程中不同阶段的解法处理与数据可用性。