一句话总结

香港科技大学的研究人员提出 LanPaint，一种无需训练、渐近精确的偏条件采样方法，适用于基于常微分方程（ODE）和修正流扩散模型，通过高效的朗之万动力学实现无需反向传播的蒙特卡洛推断，具备精确的分布匹配与高质量修复能力，在速度和视觉连贯性上优于先前方法。

主要贡献

• 现有扩散模型中无需训练的偏条件采样方法存在根本性局限，包括不可解的逆问题形式、依赖启发式损失函数或反向传播，以及与快速 ODE 采样器不兼容，导致分布匹配效果差且推断效率低下。
• LanPaint 引入一种无需训练、渐近精确的方法，利用精心设计的朗之万动力学，包含双向引导得分（bidirectional guided score），实现已知区域与修复区域之间的相互适应，并采用快速朗之万动力学方案，每步仅需 5 次内循环即可实现高保真采样。
• 在多种模型（包括 HiDream、Flux、SD 3.5 和 SD XL）上的实验表明，LanPaint 在修复质量和视觉连贯性方面表现卓越，结果通过 ODE 基采样器获得且无需梯度计算，验证了其高效性与现代扩散架构的兼容性。

引言

扩散模型在图像生成领域已占据主导地位，尤其得益于高效的 ODE 基与修正流采样器，实现了快速、确定性的采样。然而，其标准去噪机制在无需训练的偏条件采样（如已知像素下的图像修复）任务中表现不佳，因为现有方法要么依赖计算成本高昂的随机采样，要么使用无法匹配真实条件分布的启发式损失函数，或存在收敛问题与局部极小值陷阱。先前方法通常与快速 ODE 求解器不兼容，或需针对模型进行特定训练，限制了其通用性与实用性。本文作者提出 LanPaint，一种无需训练的方法，通过引入新颖的双向引导得分与快速朗之万动力学方案，实现渐近精确的偏条件采样。该方法可在每步仅 5 次内迭代下实现高保真修复，兼容 ODE 与修正流采样器，并支持无需反向传播的推断，克服了先前工作的关键局限，同时在多种扩散架构上保持优异性能。

方法

作者利用扩散模型框架解决偏条件采样挑战，尤其针对图像修复任务。该方法的核心基于去噪扩散概率模型（DDPM），其建模图像 $\mathbf{z}$z 上的联合分布 $p(\mathbf{z}) = p(\mathbf{x}, \mathbf{y})$p(z)=p(x,y)，其中 $\mathbf{x}$x 为待修复区域，$\mathbf{y}$y 为观测区域。模型通过前向扩散过程，逐步向数据添加高斯噪声，训练目标是从逐渐变噪的版本中重建干净图像 $\mathbf{z}_0$z0​。该过程由奥恩斯坦-乌伦贝克（Ornstein–Uhlenbeck, OU）随机微分方程（SDE）控制，将数据分布 $p(\mathbf{z})$p(z) 转变为纯高斯噪声分布 $\mathcal{N}(\mathbf{0}, \mathbf{I})$N(0,I)。为从学习到的分布中采样，模型需逆转该过程。后向扩散被表述为 SDE 或常微分方程（ODE），其中得分函数 $\mathbf{s}(\mathbf{z}, t) = \nabla_{\mathbf{z}} \log p_t(\mathbf{z})$s(z,t)=∇z​logpt​(z) 指导去噪过程。该得分函数通常由神经网络（如 U-Net）学习，训练目标是预测前向过程中添加的噪声。

[[IMG:|Figure 2: Comparison of inpainting methods for conditional distribution sampling (known y, inpaint x). Left: Ground truth Gaussian samples. Middle: KL divergence versus diffusion steps across methods ("-10" denotes 10 inner iterations where applicable). Right: Effect of inner iterations at 20 diffusion steps. The dashed line at KL=0.01 highlights the performance gap between asymptotically exact methods and heuristic approaches.]]

图像修复的主要挑战在于，直接采样所需的条件得分函数 $\mathbf{s}_{\mathbf{x}|\mathbf{y}_o} = \nabla_{\mathbf{x}} \log p_t(\mathbf{x}|\mathbf{y}_o)$sx∣yo​​=∇x​logpt​(x∣yo​) 无法获取。为克服此问题，作者提出一种解耦近似：$q_t(\mathbf{x}, \mathbf{y}|\mathbf{y}_o) = p_t(\mathbf{x}|\mathbf{y}) \cdot p_t(\mathbf{y}|\mathbf{y}_o)$qt​(x,y∣yo​)=pt​(x∣y)⋅pt​(y∣yo​)，该近似可计算，因为 $p_t(\mathbf{y}|\mathbf{y}_o)$pt​(y∣yo​) 可由前向过程解析获得，而 $p_t(\mathbf{x}|\mathbf{y})$pt​(x∣y) 与联合分布共享相同得分。随后，作者引入一种新方法——双向引导（Bidirectional Guided, BiG）得分，用于从该近似分布中生成样本。BiG 得分 $\mathbf{g}_{\lambda}(\mathbf{x}, \mathbf{y}, t)$gλ​(x,y,t) 的设计旨在实现修复区域 $\mathbf{x}_t$xt​ 与观测区域 $\mathbf{y}_t$yt​ 之间的双向反馈。其通过将 $\mathbf{x}_t$xt​ 的信息融入 $\mathbf{y}_t$yt​ 的采样过程，同时保留观测内容。BiG 得分定义为条件分布 $p_t(\mathbf{y}|\mathbf{y}_o)$pt​(y∣yo​) 与联合分布 $p_t(\mathbf{y}|\mathbf{x})$pt​(y∣x) 得分的组合，其中引导系数 $\lambda$λ 控制反馈强度。这使模型能够摆脱先前方法中修复区域易陷入局部极小值的问题。

[[IMG:|Figure 9: We analyze the average norm ratio between the ideal score $\mathbf{s}_{\mathbf{y}}^{*}$sy∗​ (Eq.65) and the component discarded by the BiG score, $\mathbf{s}_{\mathbf{y}}^{*}-\mathbf{g}_{\lambda}$sy∗​−gλ​, relative to $\bar{\\alpha}_{t}$alphaˉ​t​, in the conditional Gaussian case (Section 5.1). We focus on the right part of the image when $\bar{\\alpha}_{t}$alphaˉ​t​ approaches 1 (i.e., $t \\rightarrow 0$trightarrow0), which determines the distribution of generated clean image. This ratio decreases at the same rate as $\\sqrt{1-\\bar{\\alpha}_{t}}$sqrt1−baralphat​, indicating that the BiG score $\mathbf{g}_{\lambda}$gλ​ closely approximates the ideal score $\mathbf{s}_{\mathbf{y}}^{*}$sy∗​ with negligible error as $t \\rightarrow 0$trightarrow0. This confirms that the error scales as $\\mathcal{O}(\\sqrt{1-\\bar{\\alpha}_{t}})$mathcalO(sqrt1−baralphat​), laying the foundation for Theorem 4.1.]]

为高效从 BiG 得分定义的分布中采样，作者提出快速朗之万动力学（Fast Langevin Dynamics, FLD），一种欠阻尼朗之万动力学（ULD）的变体。FLD 在朗之万动力学中引入动量变量 $\mathbf{q}_{\tau}$qτ​，作为时间平均力，加速收敛至稳态分布。动力学由状态 $\mathbf{z}_{\tau} = (\mathbf{x}_{\tau}, \mathbf{y}_{\tau})$zτ​=(xτ​,yτ​) 及其动量 $\mathbf{q}_{\tau}$qτ​ 的一组 SDE 定义。关键创新在于在数值求解器中引入扩散阻尼力。该力源自前向扩散过程，确保即使在大时间步长下解仍保持稳定。FLD 求解器是动力学的解析解，将得分函数视为时间区间内的常数，且设计用于保持原始朗之万动力学的稳态分布。该方法进一步通过参数调度增强，维持恒定判别式，确保扩散过程中阻尼行为一致。这使得在更大步长下仍能实现稳定高效采样，克服了标准朗之万动力学中收敛速度与数值稳定性之间的权衡。

实验

• LanPaint 在 2D 合成高斯基准测试中验证了精确条件采样，其 KL 散度接近零，所需扩散步数与内循环步数均少于 TFG、FLD 及启发式方法（MCG、DPS、CoPaint、DDRM），后者无法将 KL 散度降至 0.01 以下。
• 在 500 组分高斯混合分布上，LanPaint 有效缓解了修复过程中的局部极大值陷阱，通过 BiG 得分在观测区域与修复区域间建立双向信息流，显著降低 KL 散度。
• 在 CelebA-HQ-256 与 ImageNet-256 上，LanPaint 在多种掩码类型（方框、半边、棋盘、外推）下均达到 SOTA 的 LPIPS 与 FID 分数，仅使用 20 步欧拉积分，优于 RePaint、TFG、DPS、CoPaint 与 MCG，且计算效率更高、内存开销极低（ImageNet 上为 599 MB，相较基于反向传播方法的 5445 MB 显著降低）。
• 消融实验确认 BiG 得分与快速朗之万动力学（FLD）对性能至关重要，尤其在 ImageNet 上，FLD 支持大步长稳定采样，而 BiG 得分提升各数据集的准确性。
• LanPaint 在生产级模型（包括 Stable Diffusion 3.5、Flux.1 Dev、HiDream-L1 与 Stable Diffusion XL）上展现出强大泛化能力，覆盖 DDPM 与修正流架构，ComfyUI 中验证了无缝修复与外推效果。
• LanPaint 可扩展至 140 亿参数的 T2V 模型（Wan 2.2）的视频修复与外推任务，在 40 帧片段上仅用 20 次扩散步与两次内迭代即实现连贯结果，展示了其维度无关的设计优势。
• LanPaint 在蒸馏模型上的性能下降，源于其对基于得分的扩散解释的依赖，且假设观测无噪声，揭示了未来研究方向：处理噪声输入与蒸馏兼容的得分学习。

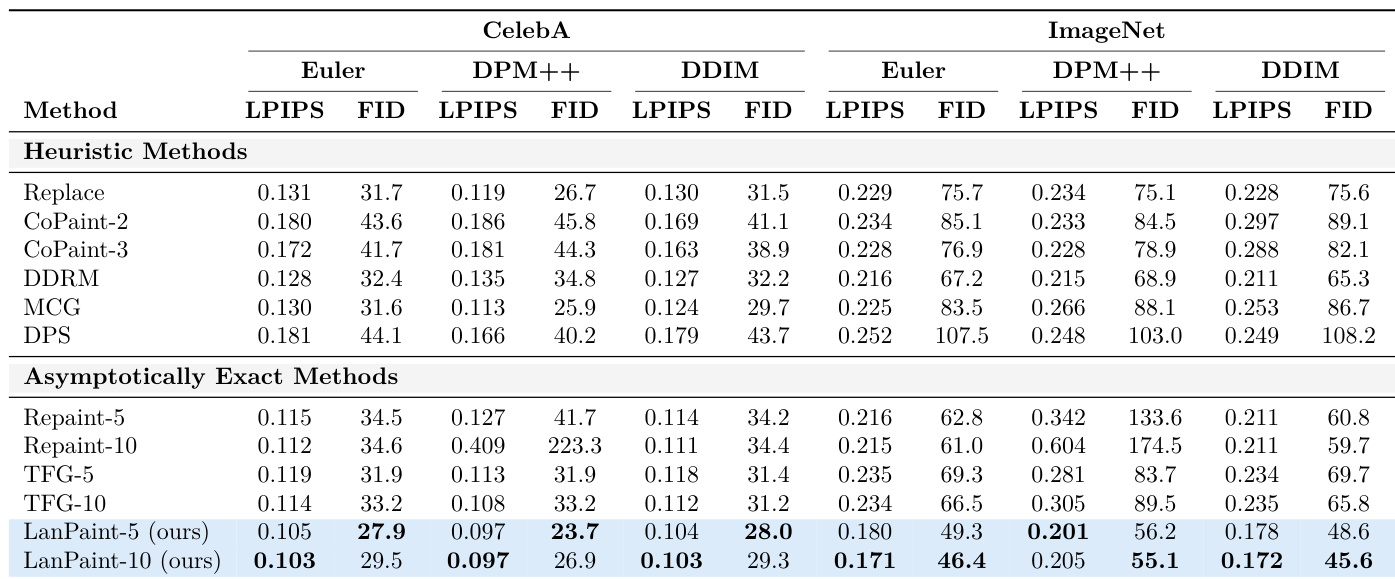
结果表明，LanPaint 在多数修复任务中实现了最低的 LPIPS 与 FID 分数，优于所有启发式与渐近精确方法。作者使用 LanPaint-10 实现最佳整体性能，在棋盘与外推场景中显著低于基线的发散度。

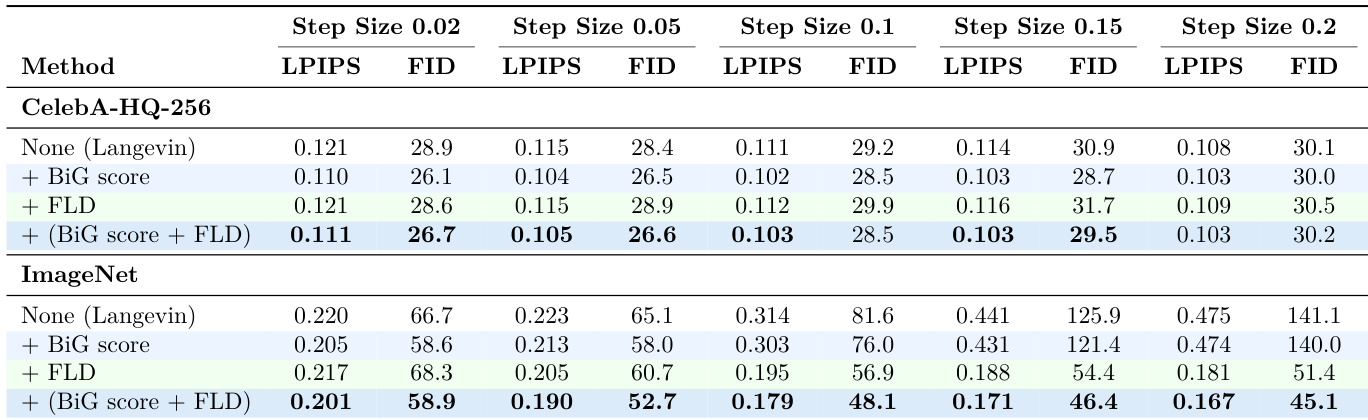
作者通过消融实验评估 BiG 得分与快速朗之万动力学（FLD）在不同步长下对 LanPaint 性能的影响。结果显示，在 CelebA-HQ-256 上，BiG 得分显著提升性能，且方法在各步长下保持稳定；而在 ImageNet 上，两个组件均至关重要，FLD 通过防止发散，使大步长下性能更优。

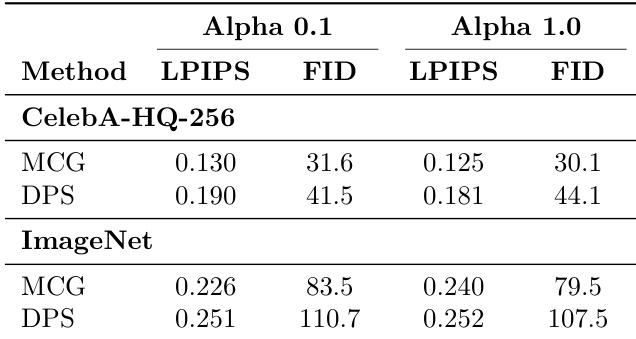
作者在消融实验中评估不同 $\alpha$α 值对 MCG 与 DPS 方法的影响。在 CelebA-HQ-256 上，两种方法在 $\alpha = 0.1$α=0.1 时 LPIPS 与 FID 分数均优于 $\alpha = 1.0$α=1.0，MCG 达到 0.125 LPIPS 与 30.1 FID，DPS 达到 0.181 LPIPS 与 44.1 FID。在 ImageNet 上，MCG 与 DPS 在 $\alpha = 0.1$α=0.1 时表现更优，分别达到 0.240 LPIPS 与 79.5 FID，以及 0.252 LPIPS 与 107.5 FID。

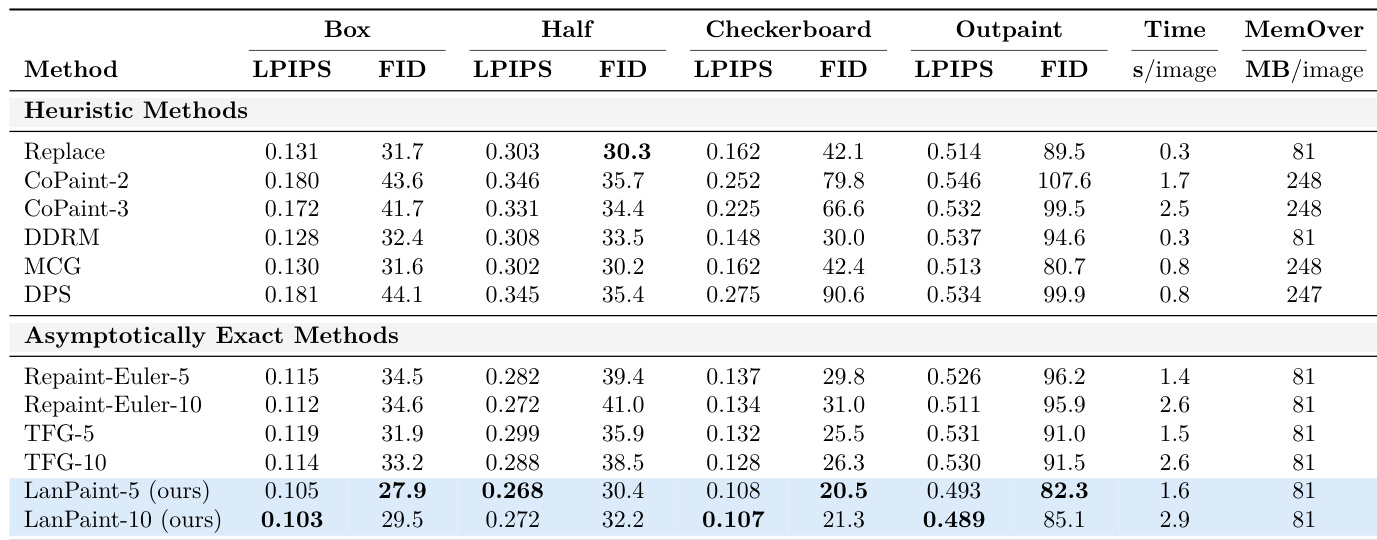
结果表明，LanPaint 在 CelebA-HQ-256 上的多数修复与外推任务中实现了最低的 LPIPS 与 FID 分数，优于所有启发式与渐近精确方法。作者使用 LanPaint-10 实现最佳性能，相比基线显著降低误差，同时保持优异的计算效率。

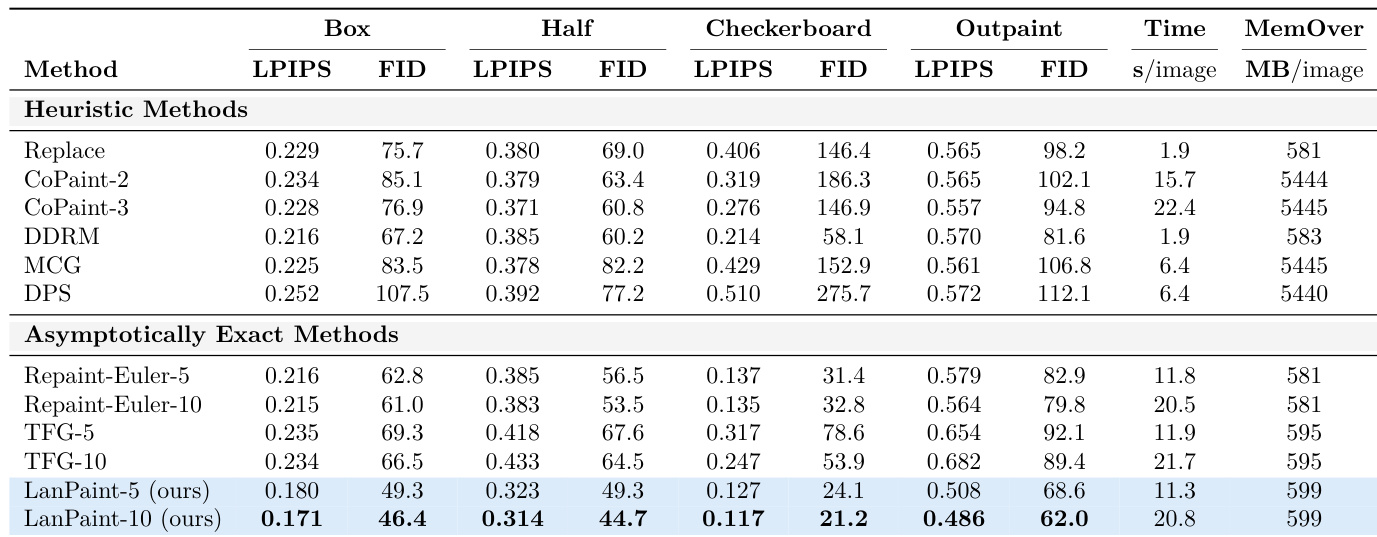
结果表明，LanPaint 在 CelebA 与 ImageNet 两个数据集上均实现最低的 LPIPS 与 FID 分数，在多数配置中优于所有启发式与渐近精确方法。作者通过表格展示，LanPaint 始终生成质量更高、感知相似性更强、特征分布对齐更优的修复图像，尤其在棋盘与外推等挑战性任务中表现突出。