一句话总结

来自巴黎-萨克雷大学和法国国家科学研究中心的作者提出了一种名为Gibbs Diffusion（GDiff）的新框架，通过在条件扩散采样器与蒙特卡洛噪声参数估计器之间交替迭代，实现对扩散模型中信号和未知噪声参数的盲后验采样。与以往需要已知噪声统计的方法不同，GDiff利用参数化高斯噪声假设和吉布斯迭代方案，联合推断信号与噪声特性，在彩色噪声下的盲图像去噪以及宇宙微波背景数据的宇宙学推断中均取得成功，实现了对早期宇宙模型的贝叶斯约束。

主要贡献

• 本文在贝叶斯框架下解决了盲去噪问题，即从观测中同时推断信号和未知噪声参数（如彩色噪声的幅度和谱指数），克服了标准扩散模型需已知噪声协方差的局限性。
• 提出了Gibbs Diffusion（GDiff），一种新颖的吉布斯采样方法，通过交替使用一个训练为将信号先验映射到噪声分布的条件扩散模型，以及一个用于噪声参数的蒙特卡洛采样器，实现对信号与噪声的联合后验推断。
• 该方法在自然图像盲去噪（未知彩色噪声）和宇宙微波背景数据的宇宙学分析中进行了验证，表现出最先进性能，并提供了关于平稳分布和误差传播的理论保证。

引言

去噪技术随着深度生成模型的发展取得了显著进步，尤其是扩散模型在学习复杂信号先验和实现后验采样方面表现出色。然而，现有方法通常需要已知的噪声特性（如幅度和协方差），限制了其在噪声参数未知的盲去噪场景中的应用。这一限制在医学成像、天文学和宇宙学等关键领域尤为突出，因为准确的噪声建模对可靠推断至关重要。作者提出了Gibbs Diffusion（GDiff），一种新框架，通过结合一个训练为将信号先验映射到噪声分布族的扩散模型，以及一个用于噪声参数推断的蒙特卡洛采样器，实现对信号和未知噪声参数的联合采样。该方法支持任意参数化高斯噪声下的盲去噪，提供了平稳分布存在的理论保证，并量化了误差传播。该方法在具有彩色噪声的自然图像去噪和宇宙微波背景数据的宇宙学分析中得到验证，其中噪声参数对应于基本的宇宙学模型。

数据集

• 数据集包含两个主要部分：ImageNet 2012中的自然图像和用于尘埃发射与CMB各向异性模拟的宇宙学数据。
• 对于自然图像，作者使用ImageNet 2012完整训练集（共1,281,167张图像），尺寸重置为3 × 256 × 256并进行中心裁剪。图像通过随机水平翻转进行增强，并归一化至[0, 1]范围。
• 宇宙学数据集源自CATS数据库（Burkhart et al., 2020），基于弥散星际介质的湍流流体动力学模拟。尘埃发射图作为气体柱密度的代理，生成991张256 × 256的模拟图，其中10%用于验证。
• CMB图通过在球面上采样高斯随机场生成，协方差矩阵Σφ由宇宙学参数φ决定，使用CAMB计算功率谱，使用pixell将结果投影到256 × 256的像素块上，像素分辨率为8'。有效天空覆盖范围约为34 × 34 deg²。
• 训练样本通过将尘埃图与CMB实现组合生成，其中宇宙学参数（H₀和ω_b）从先验分布p(φ)中采样。一个可微神经模拟器近似映射φ → Σφ，以支持HMC的高效训练和梯度计算。
• 扩散模型在ImageNet数据上训练100个周期，使用8块H100 GPU，每GPU批量大小为128，采用AdamW优化器，无学习率调度，权重衰减设为0。
• 在宇宙学应用中，训练在单块A100 80GB GPU上进行100,000个周期，批量大小为64，使用AdamW配合反平方根学习率调度器和预热机制。训练在损失达到平台期后继续进行，以提升模型精度，经基于模拟的校准验证。

方法

作者利用扩散模型在贝叶斯框架下解决盲去噪问题，将问题形式化为联合分布$p(\boldsymbol{x}, \boldsymbol{\phi} \mid \boldsymbol{y})$p(x,ϕ∣y)的后验采样。其方法核心——GDiff——是一种吉布斯采样算法，通过交替执行两个条件采样步骤，迭代构建马尔可夫链。第一步是在给定观测$\boldsymbol{y}$y和噪声参数$\boldsymbol{\phi}$ϕ的条件下采样信号$\boldsymbol{x}$x；第二步是在给定观测$\boldsymbol{y}$y和当前信号估计$\boldsymbol{x}$x的条件下采样噪声参数$\boldsymbol{\phi}$ϕ。该迭代过程旨在经过足够多的迭代后，生成目标联合后验分布的样本。

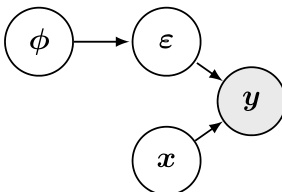
上图中的图模型展示了盲去噪问题背后的生成过程。它表明观测数据$\boldsymbol{y}$y由真实信号$\boldsymbol{x}$x和噪声参数$\boldsymbol{\phi}$ϕ生成，而$\boldsymbol{\phi}$ϕ进一步生成噪声$\boldsymbol{\varepsilon}$ε。目标是从观测$\boldsymbol{y}$y中推断潜在变量$\boldsymbol{x}$x和$\boldsymbol{\phi}$ϕ，这是一个经典的贝叶斯推断问题。GDiff算法通过构建一个探索联合后验分布$p(\boldsymbol{x}, \boldsymbol{\phi} \mid \boldsymbol{y})$p(x,ϕ∣y)的马尔可夫链，直接针对该推断任务。

第一采样步骤$p(\boldsymbol{x} \mid \boldsymbol{y}, \boldsymbol{\phi})$p(x∣y,ϕ)通过扩散模型解决。作者表明，扩散模型可被训练以同时定义先验$p(\boldsymbol{x})$p(x)，并提供一种高效采样后验分布$p(\boldsymbol{x} \mid \boldsymbol{y}, \boldsymbol{\phi})$p(x∣y,ϕ)的方法。这是通过训练模型逆转一个前向随机过程实现的，该过程逐步向数据添加噪声。前向过程由一个建模信号$\boldsymbol{x}$x随时间噪声化的随机微分方程（SDE）定义。扩散模型学习近似该过程的反向SDE，从而实现从后验分布生成样本。实践中，扩散模型以噪声参数$\boldsymbol{\phi}$ϕ为条件，这些参数作为得分网络的输入，使模型能够处理与先验$p(\boldsymbol{\phi})$p(ϕ)一致的多种噪声配置。

第二采样步骤$p(\boldsymbol{\phi} \mid \boldsymbol{y}, \boldsymbol{x})$p(ϕ∣y,x)等价于采样$p(\boldsymbol{\phi} \mid \boldsymbol{\varepsilon})$p(ϕ∣ε)，其中$\boldsymbol{\varepsilon} = \boldsymbol{y} - \boldsymbol{x}$ε=y−x为残差噪声。该步骤使用哈密顿蒙特卡洛（HMC）采样器完成。HMC算法需要高效评估和微分对数后验分布$\log p(\boldsymbol{\phi} \mid \boldsymbol{\varepsilon})$logp(ϕ∣ε)，其由对数先验$\log p(\boldsymbol{\phi})$logp(ϕ)和对数似然$\log p(\boldsymbol{\varepsilon} \mid \boldsymbol{\phi})$logp(ε∣ϕ)组成。对于所考虑的高斯噪声模型，对数似然具有闭式表达，实现简单。HMC采样器构建一个马尔可夫链，一旦进入平稳状态，即可生成目标分布$p(\boldsymbol{\phi} \mid \boldsymbol{\varepsilon})$p(ϕ∣ε)的样本。

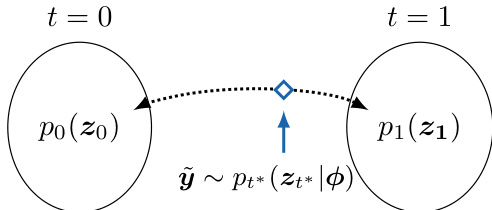
上图展示了反向SDE过程，这是扩散模型能够从后验采样核心所在。它显示了从初始分布$p_0(\boldsymbol{z}_0)$p0​(z0​)（对应先验$p(\boldsymbol{x})$p(x)）到最终分布$p_1(\boldsymbol{z}_1)$p1​(z1​)（高度噪声分布）的转换。反向过程从时间$t=1$t=1处的点$\tilde{\boldsymbol{y}}$y~​开始，反向流动以生成来自后验分布$p(\boldsymbol{x} \mid \boldsymbol{y}, \boldsymbol{\phi})$p(x∣y,ϕ)的样本。该过程由一个依赖于当前分布得分函数的反向SDE定义，扩散模型学习近似该得分函数。算法在两个步骤间迭代运行，使用扩散模型采样信号，使用HMC采样器采样噪声参数，从而生成联合后验分布的样本。

实验

• 在具有彩色噪声的自然图像盲去噪和包含银河系前景的CMB数据宇宙学推断任务上进行评估，展示了吉布斯采样器在两种场景下的有效收敛。
• 在基于ImageNet的去噪任务中，GDiff在后验均值下达到SSIM 0.896，在后验样本下达到0.882，优于在白噪声上训练的DnCNN，并与非盲的BM3D方法相当，尽管其为盲去噪方法。
• 在CMB数据上，该方法成功推断噪声参数并恢复后验分布，但因扩散模型近似误差导致轻微偏差。
• 基于引导的方法（DPS、II-GDM）因噪声协方差的高条件数（约6 × 10⁵）导致数值不稳定性，造成后验估计不佳和吉布斯采样无法收敛。
• 有效推断需要时间依赖的正则化，但即便如此，大尺度结构恢复效果仍差，凸显了现有引导方法在高动态范围逆问题中的局限性。

结果表明，GDiff在不同噪声类型和水平下与BM3D和DnCNN相比具有竞争力的图像质量，SSIM值接近或超过非盲BM3D方法。该方法在盲去噪和参数估计中均表现稳定，后验采样指标稳定，且在各种噪声条件下均能有效恢复无噪声图像。

结果表明，GDiff在不同噪声类型和水平下与BM3D和DnCNN相比表现出竞争性或更优性能，最佳结果出现在白噪声条件下。该方法在盲去噪中表现出鲁棒性，生成高质量重建结果并提供准确的后验估计，尽管性能随噪声模型和数据集变化而有所不同。