One-Sentence Summary

Researchers from Peking University and DeepSeek-AI introduce Engram, a scalable conditional memory module with O(1) lookup that complements MoE by offloading static knowledge retrieval, freeing early Transformer layers for deeper reasoning and delivering consistent gains across reasoning (BBH +5.0, ARC-Challenge +3.7), code and math (HumanEval +3.0, MATH +2.4), and long-context tasks (Multi-Query NIAH: 84.2 → 97.0), while maintaining iso-parameter and iso-FLOPs efficiency.

---

Key Contributions

• Conditional memory as a new sparsity axis. The paper introduces conditional memory as a complement to MoE, realized via Engram—a modernized N-gram embedding module enabling O(1) retrieval of static patterns and reducing reliance on neural computation for knowledge reconstruction.

• Principled scaling via sparsity allocation. Guided by a U-shaped scaling law from the Sparsity Allocation problem, Engram is scaled to 27B parameters and surpasses iso-parameter and iso-FLOPs MoE baselines on MMLU (+3.4), BBH (+5.0), HumanEval (+3.0), and Multi-Query NIAH (84.2 → 97.0).

• Mechanistic and systems insights. Analysis shows Engram increases effective network depth by offloading static reconstruction from early layers and reallocating attention to global context, improving long-context retrieval while enabling infrastructure-aware efficiency through decoupled storage and compute.

---

Introduction

Transformers often simulate knowledge retrieval through expensive computation, wasting early-layer capacity on reconstructing static patterns such as named entities or formulaic expressions. Prior approaches either treat N-gram lookups as external augmentations or embed them only at the input layer, limiting their usefulness in sparse, compute-optimized architectures like MoE.

The authors propose Engram, a conditional memory module that modernizes N-gram embeddings for constant-time lookup and injects them into deeper layers of the network to complement MoE. By formulating a Sparsity Allocation problem, they uncover a U-shaped scaling law that guides how parameters should be divided between computation (MoE) and memory (Engram). Scaling Engram to 27B parameters yields strong gains not only on knowledge benchmarks, but also on reasoning, coding, and math tasks.

Mechanistic analyses further show that Engram frees early layers for higher-level reasoning and substantially improves long-context modeling. Thanks to deterministic addressing, its memory can be offloaded to host storage with minimal overhead, making it practical at very large scales.

---

Method

Engram augments a Transformer by structurally decoupling static pattern storage from dynamic computation. It operates in two phases—retrieval and fusion—applied at every token position.

Engram is inserted between the token embedding layer and the attention block, and its output is added through a residual connection before MoE.

---

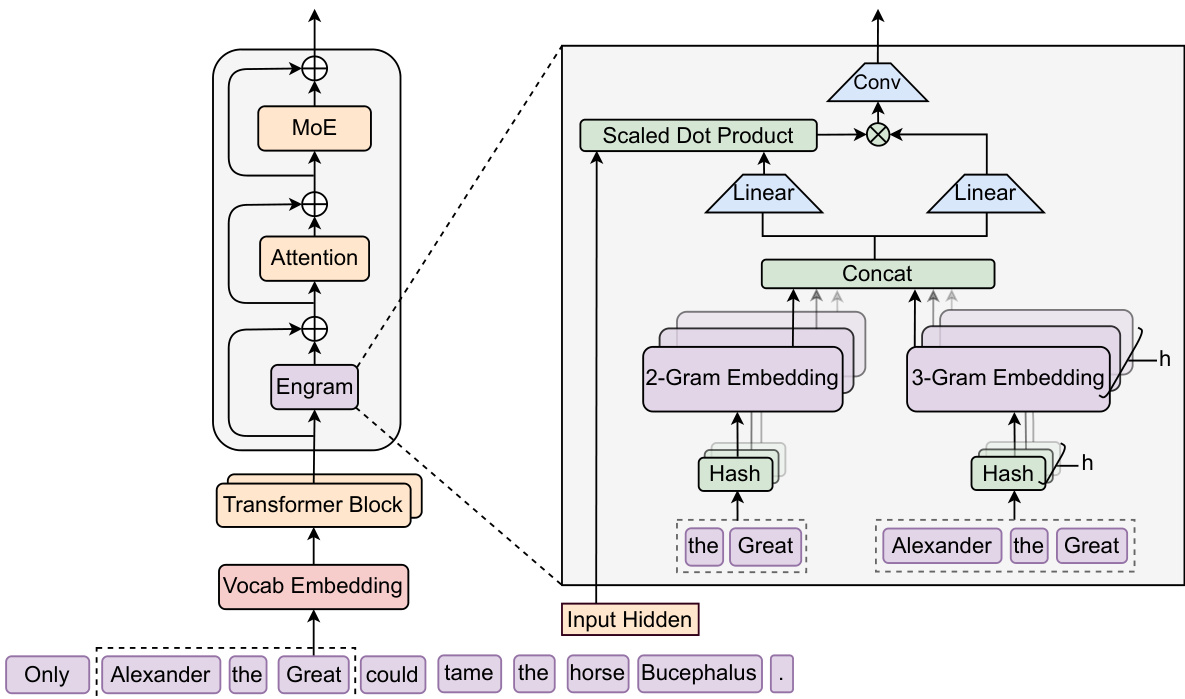
Retrieval Phase

1. Canonicalization.
   Tokens are mapped to canonical IDs using a vocabulary projection layer $\mathcal{P}$P (e.g., NFKC normalization and lowercasing), reducing effective vocabulary size by 23% for a 128k tokenizer.

2. N-gram construction.
   For each position $t$t, suffix N-grams $g_{t,n}$gt,n​ are formed from canonical IDs.

3. Multi-head hashing.
   To avoid parameterizing the full combinatorial N-gram space, the model uses $K$K hash functions $varphi_{n,k}$varphin,k​ to map each N-gram into a prime-sized embedding table $\mathbf{E}_{n,k}$En,k​, retrieving embeddings $\mathbf{e}_{t,n,k}$et,n,k​.

4. Concatenation.
   The final memory vector is

$$\mathbf{e}_t \triangleq \bigsqcup_{n=2}^{N} \bigsqcup_{k=1}^{K} \mathbf{e}_{t,n,k}.$$et​≜n=2⨆N​k=1⨆K​et,n,k​.

---

Fusion Phase

The static memory vector $\mathbf{e}_t$et​ is modulated by the current hidden state $\mathbf{h}_t$ht​:

$$\mathbf{k}_t = \mathbf{W}_K \mathbf{e}_t, \qquad \mathbf{v}_t = \mathbf{W}_V \mathbf{e}_t .$$kt​=WK​et​,vt​=WV​et​.

A scalar gate controls the contribution:

$$\alpha_t = \sigma \left( \frac{ \mathrm{RMSNorm}(\mathbf{h}_t)^\top \mathrm{RMSNorm}(\mathbf{k}_t) }{\sqrt{d}} \right).$$αt​=σ(d​RMSNorm(ht​)⊤RMSNorm(kt​)​).

The gated value $\tilde{\mathbf{v}}_t = \alpha_t \cdot \mathbf{v}_t$v~t​=αt​⋅vt​ is refined using a depthwise causal convolution:

$$\mathbf{Y} = \mathrm{SiLU}\!\left( \mathrm{Conv1D}(\mathrm{RMSNorm}(\tilde{\mathbf{V}})) \right) + \tilde{\mathbf{V}}.$$Y=SiLU(Conv1D(RMSNorm(V~)))+V~.

This output is added back to the hidden state before attention and MoE layers.

---

Multi-branch Parameter Sharing

For architectures with multiple branches:

• Embedding tables and $\mathbf{W}_V$WV​ are shared.
• Each branch (m) has its own $\mathbf{W}_K^{(m)}$WK(m)​:

$$\alpha_t^{(m)} = \sigma \left( \frac{ \mathrm{RMSNorm}(\mathbf{h}_t^{(m)})^\top \mathrm{RMSNorm}(\mathbf{W}_K^{(m)} \mathbf{e}_t) }{\sqrt{d}} \right).$$αt(m)​=σ(d​RMSNorm(ht(m)​)⊤RMSNorm(WK(m)​et​)​).

Outputs are fused into a single dense FP8 matrix multiplication for GPU efficiency.

---

System Design

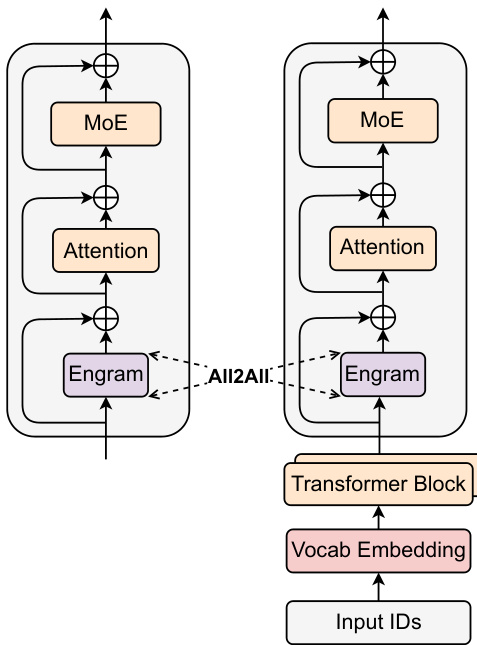
Training

Embedding tables are sharded across GPUs. Active rows are retrieved using All-to-All communication, enabling linear scaling of memory capacity with the number of accelerators.

Inference

Deterministic addressing allows embeddings to be offloaded to host memory:

• Asynchronous PCIe prefetch overlaps memory access with computation.
• A multi-level cache exploits the Zipfian distribution of N-grams.
• Frequent patterns remain on fast memory; rare ones reside on high-capacity storage.

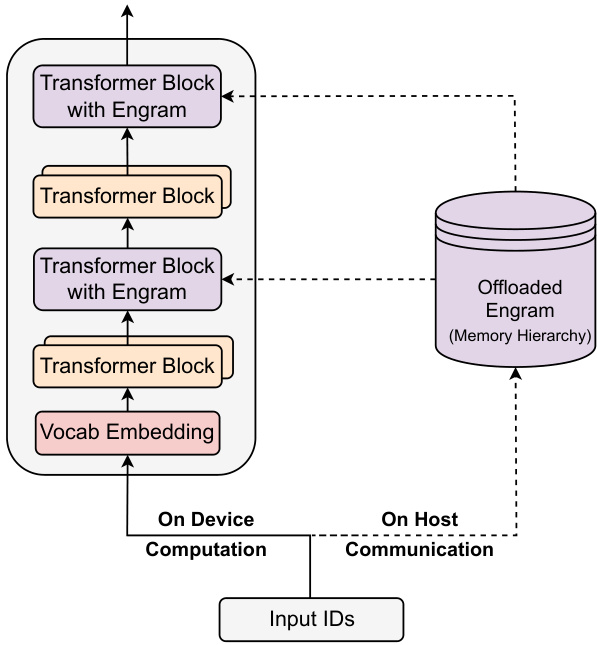
This design enables massive memory capacity with negligible impact on effective latency.

---

Experiments

Parameter Allocation

Under compute-matched settings, allocating 75–80% of sparse parameters to MoE and the remainder to Engram yields optimal results, outperforming pure MoE baselines:

• Validation loss at 10B scale: 1.7109 (Engram) vs. 1.7248 (MoE).

Scaling Engram’s memory under fixed compute produces consistent power-law improvements and outperforms OverEncoding.

---

Benchmark Performance

Engram-27B (26.7B parameters) surpasses MoE-27B under identical FLOPs:

• BBH: +5.0
• HumanEval: +3.0
• MMLU: +3.0

Scaling to Engram-40B further reduces pre-training loss to 1.610 and improves most benchmarks.

All sparse models (MoE and Engram) substantially outperform a dense 4B baseline under iso-FLOPs.

---

Long-Context Evaluation

Engram-27B consistently outperforms MoE-27B on LongPPL and RULER benchmarks:

• Best performance on Multi-Query NIAH and Variable Tracking.
• At 41k steps (82% of MoE FLOPs), Engram already matches or exceeds MoE.

---

Inference Throughput with Memory Offload

Offloading a 100B-parameter Engram layer to CPU memory incurs minimal slowdown:

• 4B model: 9,031 → 8,858 tok/s
• 8B model: 6,316 → 6,140 tok/s (2.8% drop)

Deterministic access enables effective prefetching, masking PCIe latency.

---

Conclusion

Engram introduces conditional memory as a first-class sparsity mechanism, complementing MoE by separating static knowledge storage from dynamic computation. It delivers:

• Strong gains in reasoning, coding, math, and long-context retrieval.
• Better utilization of early Transformer layers.
• Scalable, infrastructure-friendly memory via deterministic access and offloading.

Together, these results suggest that future large language models should treat memory and computation as independently scalable resources, rather than forcing all knowledge into neural weights.