Command Palette
Search for a command to run...
إلى بحوث الرياضيات المستقلة
إلى بحوث الرياضيات المستقلة
الملخص
لقد أسفرت التطورات الحديثة في النماذج الأساسية عن أنظمة استدلال قادرة على تحقيق مستوى الميدالية الذهبية في أولمبياد الرياضيات الدولي. ومع ذلك، فإن الانتقال من حل المشكلات على مستوى المسابقات إلى البحث المهني يتطلب التفاعل مع كمّ هائل من الأدبيات وبناء براهين ذات أفق طويل. في هذه الدراسة، نقدّم "أليثيا" (Aletheia)، وهي وكيل بحث رياضي يُولِّد ويوثّق ويُعدّل الحلول بشكل تكراري ونهائي باللغة الطبيعية. وبشكل خاص، يعتمد أليثيا على ثلاث مصادر رئيسية: (أ) نسخة متطورة من نموذج Gemini Deep Think لحل المشكلات المعقدة في الاستدلال؛ (ب) قانون توسُّع جديد يتم تطبيقه أثناء الاستدلال، يمتد ليتجاوز مشكلات المستوى الأولمبيادي؛ (ج) استخدام مكثف للأدوات لاستكشاف تعقيدات البحث الرياضي. ونُظهر قدرة أليثيا على التحول من حل مسائل أولمبياد إلى تمارين على مستوى الدكتوراه، وبشكل لافت، من خلال عدة مراحل بارزة في البحث الرياضي المدعوم بالذكاء الاصطناعي: (أ) ورقة بحثية (Feng26) أُنتجت بالكامل بواسطة الذكاء الاصطناعي دون أي تدخل بشري في حساب ثوابت هيكلية معينة في الهندسة الحسابية تُعرف بـ"الوزن الذاتي" (eigenweights)؛ (ب) ورقة بحثية (LeeSeo26) تُظهر تعاونًا بين الإنسان والذكاء الاصطناعي في إثبات حدود لنظم الجسيمات المتفاعلة تُعرف بـ"المجموعات المستقلة" (independent sets)؛ (ج) تقييم شبه ذاتي مكثف (Feng et al., 2026a) لـ 700 مشكلة مفتوحة من قاعدة بيانات مُ conjecture إردوش (Bloom’s Erdős Conjectures)، بما في ذلك حلول ذاتية لـ أربع مشكلات مفتوحة. ولمساعدة الجمهور على فهم أفضل للتطورات المتعلقة بالذكاء الاصطناعي والرياضيات، نقترح تحديد مستويات معيارية للذاتية (الاستقلالية) ودرجة الأصالة في النتائج المدعومة بالذكاء الاصطناعي، كما نقدّم مفهومًا جديدًا يُعرف ببطاقات التفاعل بين الإنسان والذكاء الاصطناعي بهدف تعزيز الشفافية. ونختتم بتأملات حول التعاون بين الإنسان والذكاء الاصطناعي في مجال الرياضيات.
One-sentence Summary
Google DeepMind researchers introduce Aletheia, an autonomous mathematical research agent powered by an advanced Gemini Deep Think model, a novel inference-time scaling law, and tool-augmented reasoning with web search and Python, which achieves state-of-the-art performance on IMO-ProofBench (95.1%) and FutureMath Basic, and delivers three landmark milestones: a fully AI-generated paper on eigenweights in arithmetic geometry (Feng26), a human-AI collaborative proof on independent sets (LeeSeo26), and autonomous solutions to four open Erdős conjectures—distinguishing itself from formal-methods systems by operating end-to-end in natural language with iterative generation, verification, and revision.
Key Contributions
- The paper introduces specialized math reasoning agents that integrate informal natural language verification to bridge the gap between unreliable LLM reasoning and underdeveloped formal systems in mathematical research.
- It establishes a framework for human-AI collaboration in mathematics by demonstrating a strategy that guarantees success with at most two penalty points in a 3002-row, 3001-column adversarial grid with 3000 traps.
- The work confirms that AI can augment, not replace, mathematicians—showing that human oversight remains essential for correcting hallucinations and guiding problem formulation in current systems.
Introduction
The authors leverage advanced language models to bridge the gap between competition-level mathematical reasoning and autonomous research, where solving open problems requires synthesizing vast, specialized literature rather than answering self-contained contest questions. Prior systems, even those achieving gold-medal performance at the International Mathematical Olympiad, struggle with hallucinations and shallow understanding due to limited exposure to research-grade mathematical content. To overcome these limitations, the authors introduce Aletheia, a math research agent that combines an enhanced reasoning model, a novel inference-time scaling law, and intensive tool use—including web browsing and search—to iteratively generate, verify, and revise proofs in natural language. Aletheia achieves milestone results: autonomously deriving eigenweights in arithmetic geometry, enabling human-AI collaboration on bounds for independent sets, and solving four long-open Erdős problems, while the team proposes a taxonomy of autonomy levels and human-AI interaction cards to standardize transparency and evaluation in AI-assisted mathematics.
Method
The Aletheia agent, powered by Gemini Deep Think, employs a multi-agent iterative framework designed to solve research-level mathematical problems through a structured cycle of generation, verification, and revision. The overall architecture consists of three primary subagents: a Generator, a Verifier, and a Reviser, which operate in a closed-loop process until a solution is validated or a maximum number of attempts is reached. The framework begins with a problem input, which is processed by the Generator to produce a candidate solution. This solution is then evaluated by the Verifier, which assesses its correctness. If the solution is deemed correct, it is finalized as the output. Otherwise, if minor fixes are required, the solution is passed to the Reviser, which modifies the candidate solution before returning it to the Generator for re-evaluation. This iterative refinement continues until the Verifier approves the solution or the attempt limit is exhausted.
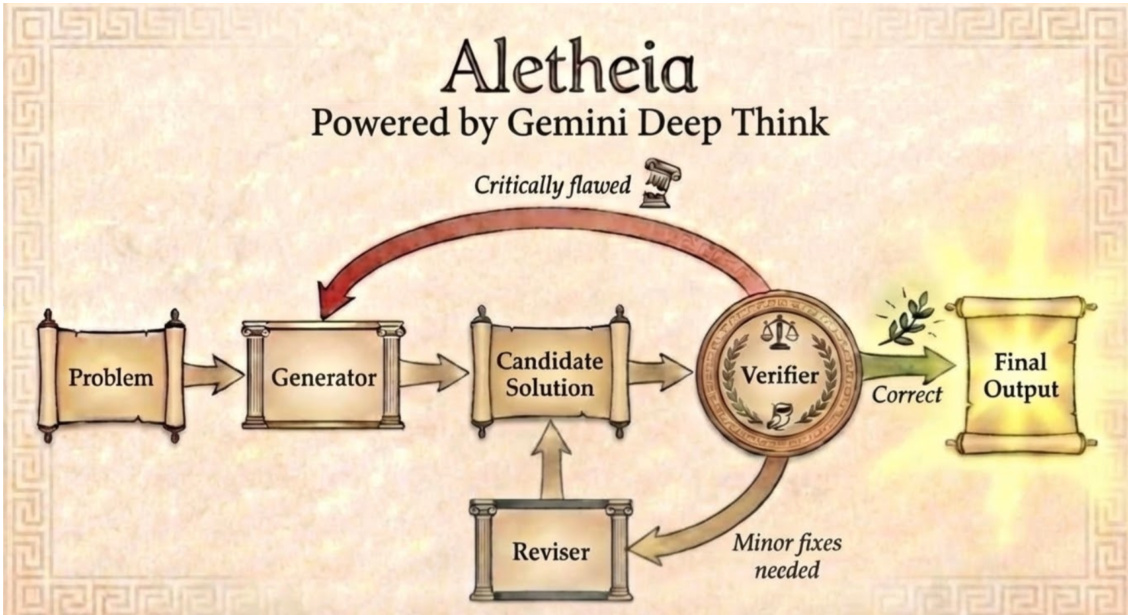
Each subagent in the system is internally orchestrated through calls to the Gemini base model, enabling the agent to leverage advanced language understanding and reasoning capabilities. The Generator is responsible for producing initial or revised candidate solutions, while the Verifier evaluates the logical consistency and correctness of these solutions. The Reviser handles the refinement of solutions based on feedback from the Verifier, ensuring that the generated content is progressively improved. This modular design allows Aletheia to address the challenges of research-level mathematics, where solutions often require deep domain knowledge and sophisticated reasoning beyond standard high school curricula. The system operates end-to-end in natural language, distinguishing it from formal language-based approaches such as AlphaGeometry and AlphaProof. The iterative nature of the framework enables Aletheia to iteratively generate, verify, and revise solutions, ultimately producing high-quality outputs that meet the rigorous standards of mathematical research.
Experiment
Experiments evaluated the scaling of inference compute on Olympiad- and PhD-level math problems, revealing that while increased compute improves accuracy on competition problems, it plateaus and fails to resolve the hallucinations and misinterpretations prevalent in research-grade reasoning. The introduction of Aletheia, an agentic framework with explicit verification and tool use, significantly outperformed prior models by reducing erroneous outputs and admitting failure when uncertain, though it still struggled with subtle citation errors and misinterpretations of open-ended problems. Case studies on Erdős conjectures showed that while AI can produce technically correct solutions, most are mathematically trivial or misaligned with problem intent, highlighting that current systems excel at retrieval and manipulation rather than genuine creativity or deep understanding.
The authors conducted ablation studies to compare the performance of Gemini Deep Think against Aletheia on research problems. Results show that Deep Think successfully reproduced some solutions but failed on others, particularly on more complex prompts, despite using similar compute. The comparison highlights Aletheia's superior performance in solving research-level problems. Gemini Deep Think successfully reproduced some solutions but failed on others, especially on complex prompts. Deep Think used similar compute but performed worse than Aletheia on most research problems. Aletheia demonstrated superior performance in solving research-level problems compared to Deep Think.

The the the table summarizes the outcomes of Aletheia's performance on a set of Erdős problems, indicating which problems were correctly solved and which were not. The results show a mix of successful and failed attempts, with some problems marked as correctly solved and others as incorrect or ambiguous. Aletheia successfully solved several Erdős problems, as indicated by the checkmarks in the the the table. Some problems were marked as incorrect, with red X's indicating failed attempts. The the the table includes a range of problems, with varying outcomes, reflecting the model's performance across different challenges.

The the the table summarizes the evaluation of 200 AI-generated solutions to Erdős problems, categorizing them into fundamentally flawed, technically correct, and meaningfully correct. Results show that the majority of solutions were flawed, with only a small fraction being both technically and meaningfully correct. Most AI-generated solutions were fundamentally flawed, making up the majority of the evaluated candidates. A minority of solutions were technically correct, but only a small subset addressed the intended problem correctly. The evaluation highlights significant challenges in achieving meaningful correctness in AI-generated mathematical solutions.

Ablation studies compared Gemini Deep Think and Aletheia on research-level problems, revealing that Aletheia consistently outperformed Deep Think, especially on complex prompts, despite similar computational resources. Evaluation of AI-generated solutions to Erdős problems showed that most were fundamentally flawed, with only a small fraction achieving both technical and meaningful correctness, underscoring persistent challenges in generating reliable mathematical reasoning.