Command Palette
Search for a command to run...
تسريع البحث العلمي باستخدام جيمي: دراسات حالة وتقنيات شائعة
تسريع البحث العلمي باستخدام جيمي: دراسات حالة وتقنيات شائعة
الملخص
أصبحت التطورات الحديثة في النماذج اللغوية الكبيرة (LLMs) تُوسع آفاقًا جديدة لتسريع البحث العلمي. وعلى الرغم من أن هذه النماذج أصبحت قادرة بشكل متزايد على مساعدة الباحثين في المهام الروتينية، فإن قدرتها على المساهمة في اكتشافات رياضية مبتكرة ومستوى خبراء ما زالت غير مفهومة تمامًا. نقدّم مجموعة من دراسات الحالة التي تُظهر كيف تمكّن الباحثون من التعاون بنجاح مع نماذج ذكاء اصطناعي متقدمة، وبخاصة النماذج المستندة إلى جوجل جيميني (خاصة نموذج جيميني ديب ثينك ومتغيراته المتقدمة)، من حل مسائل مفتوحة، ودحض افتراضات، وإنتاج أدلة جديدة في مجالات متنوعة من علوم الحاسوب النظرية، فضلاً عن مجالات أخرى مثل الاقتصاد، والتحسين، والفيزياء. واستنادًا إلى هذه التجارب، نستخلص تقنيات شائعة لتعزيز التعاون الفعّال بين الإنسان والذكاء الاصطناعي في البحث النظري، مثل التحسين التدريجي، وتفكيك المشكلات، ونقل المعرفة عبر التخصصات. ورغم أن معظم نتائجنا تنبع من منهجية تفاعلية ومحادثاتية، فإننا نسلط الضوء أيضًا على حالات محددة تتجاوز واجهات الدردشة القياسية، مثل استخدام النموذج كمُقيّم مُعاكس صارم للكشف عن عيوب دقيقة في الأدلة الحالية، أو دمجه في حلقة "عصبية-رمزية" (neuro-symbolic) تُكتب وتنفّذ الكود بشكل تلقائي للتحقق من الاستنتاجات المعقدة. تُبرز هذه الأمثلة معًا الإمكانات الكامنة للذكاء الاصطناعي ليس كأداة للاستبدال التلقائي فقط، بل كشريك مرن وحقيقي في العملية الإبداعية للاكتشاف العلمي.
One-sentence Summary
Researchers from Google and multiple universities demonstrate how Gemini-based models, via iterative refinement and neuro-symbolic loops, collaboratively solve open problems across CS, physics, and economics, elevating AI from automation tool to creative partner in theoretical discovery.
Key Contributions
- Researchers demonstrate that Gemini-based LLMs can meaningfully contribute to expert-level mathematical discovery by solving open problems, refuting conjectures, and generating proofs across theoretical computer science, economics, and physics through iterative, conversational collaboration.
- The paper introduces novel methodological frameworks including neuro-symbolic loops that autonomously write and debug code for verification, and adversarial review modes that detect subtle flaws in proofs—extending beyond chat interfaces to enable rigorous, agentic research assistance.
- Case studies across domains—from cosmic string spectra to submodular welfare and NP-hardness results—show measurable progress on longstanding problems, validated through real-world deployment and peer-reviewed outcomes, establishing reproducible patterns for human-AI co-discovery.
Introduction
The authors leverage advanced Gemini-based LLMs—not as passive tools but as active collaborators—to accelerate theoretical research across computer science, physics, and economics. While prior work has explored LLMs for automating routine tasks or solving isolated math problems, most lacked systematic methodology or broad applicability to deep, open theoretical questions. The authors address this by documenting real-world case studies where Gemini helped solve long-standing conjectures, generate novel proofs, and detect subtle bugs in peer-reviewed work—often through iterative, conversational refinement rather than one-shot prompting. Their main contribution is a practical “playbook” of techniques: iterative prompting with error correction, cross-disciplinary idea synthesis, adversarial proof review, neuro-symbolic loops for automated verification, and context de-identification to bypass model conservatism. These methods enable researchers to treat LLMs as tireless junior collaborators who synthesize vast literature, propose non-obvious connections, and accelerate discovery—without requiring specialized wrappers or custom architectures.
Dataset

The authors use a dataset composed entirely of error messages indicating “Request queue full,” sourced from system logs or API failure records. Each entry includes a title (e.g., “119. Error: Request queue full”) and a content list of repeated error strings, sometimes wrapped in LaTeX-style math delimiters (e.g., “\nError:Requestqueuefull\n”).
Key details:
- Dataset contains 8 distinct entries, each representing a unique log or request batch.
- Content length varies per entry, ranging from 2 to over 100 repetitions of the same error string.
- No filtering rules are applied; all instances are retained as-is.
- No metadata is constructed beyond the title and raw content.
- No cropping or preprocessing is performed; the data is used in its original form.
The paper does not describe training splits, mixture ratios, or model usage of this dataset. It appears to be a placeholder or error state representation rather than a functional training corpus.
Method
The authors leverage a sophisticated, multi-stage reasoning architecture centered around an advanced version of the Gemini Deep Think model. This framework is designed to handle complex mathematical problems by combining broad solution-space exploration with deep, iterative verification. The core methodology involves an initial problem statement being fed into the Gemini Agent, which then undertakes an extensive exploration of the solution space. This phase is characterized by parallel thinking, where the model simultaneously investigates multiple proof branches and solution strategies, a capability that mirrors tree-based search methods known to be effective in mathematical reasoning. This approach allows the model to synthesize diverse lines of inquiry before converging on a final, well-supported answer, rather than following a single, linear chain of thought.
Following this exploratory phase, the model engages in deep reasoning, applying its enhanced capabilities to construct rigorous arguments, formal proofs, or complex derivations. This stage is where the model's training on multi-step reasoning and theorem-proving data is most evident, enabling it to tackle intricate logical structures. The final stage of the pipeline is a robust verification loop, which combines automated checks with human expert validation. This is implemented as a long, linear chain of interactive verification calls, ensuring that the reasoning is not only deep but also correct. The entire process is iterative, with the model capable of refining its output based on human feedback, creating a dynamic, collaborative problem-solving environment.
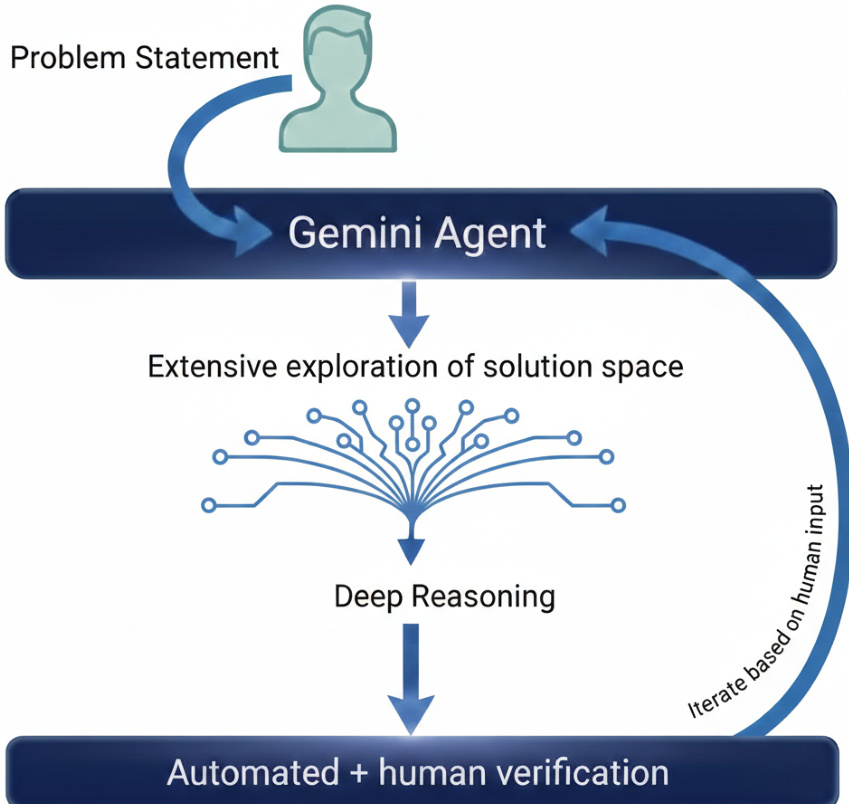
To further ground its reasoning in mathematical reality and mitigate hallucinations, the authors deploy a neuro-symbolic pipeline. In this setup, the model acts as an agent within an automated programmatic loop. It begins by generating a symbolic mathematical hypothesis or intermediate expression. It then autonomously writes an executable script, typically in Python, to evaluate this proposal against a known numerical baseline. The system executes the code, and if the execution fails, reveals numerical instability, or produces an incorrect result, the error traceback is captured and injected back into the model's context window. This feedback loop allows the model to self-correct its algebraic manipulations and prune invalid reasoning branches without requiring constant human intervention, effectively creating a self-improving, grounded reasoning system.
In specific applications, the model's reasoning is augmented by external tools and formal methods. For instance, when constructing proofs, the model can be tasked with identifying necessary external theorems, which a researcher then validates using external sources like textbooks or search engines. The model then incorporates these verified statements to generate a self-contained, rigorous proof. Similarly, for conjecture validation, the model can be directed to construct counterexamples by generating specific instances (like graphs or matrices) or to verify small cases by writing and running code to computationally check a conjecture for small values of n. This combination of internal reasoning, external validation, and automated feedback creates a powerful, multi-faceted approach to mathematical discovery and verification.
Experiment
- AI autonomously refuted a mathematical conjecture by constructing a counterexample with minimal dimensions, defining valid submodular functions, and performing exhaustive verification without human intervention.
- AI identified a critical flaw in a cryptographic proof by detecting a mismatch between perfect consistency in definition and statistical consistency in construction, validated by domain experts.
- AI solved a geometric variance problem by applying advanced tools from measure theory and functional analysis, justifying steps with foundational theorems.
- AI improved a Steiner tree conjecture analysis by recognizing and applying the Kirszbraun Extension Theorem, revealing a novel connection in high-dimensional geometry.
- AI enhanced a graph theory bound by linking it to the Bethe permanent and spectral graph theory, synthesizing cross-disciplinary methods from statistical physics and number theory.
- AI derived a tighter coreset size bound by eliminating a logarithmic factor, achieving a known optimal form.
- AI refined an approximation algorithm’s guarantee by identifying state-dependent thresholds, proving monotonicity, and connecting recurrence analysis to algorithmic correctness.
- AI contributed to local search complexity by designing algorithms, proving bounds, and generalizing results across graph structures, despite occasional hallucinations.
- AI delivered a closed-form analytic solution in cosmic string physics, replacing expensive numerical methods with stable, exact expressions matching high-precision benchmarks.
The authors use an AI model to discover a new method for evaluating cosmic string radiation integrals, achieving a stable, closed-form analytic solution with constant-time complexity. This approach eliminates numerical instability and avoids expensive matrix operations, outperforming prior techniques in both efficiency and robustness. The result resolves a longstanding computational bottleneck in the field.

The authors use a minimal counterexample with three items and two agents to refute a conjecture about submodular valuations. Results show that the expected residual welfare exceeds the proposed upper bound, invalidating the conjecture and revealing deeper complexity in how duplicated items interact with greedy allocations. This demonstrates the model’s ability to autonomously construct and verify non-trivial counterexamples without human intervention.