One-sentence Summary

The Meituan LongCat Team introduces LongCat-Flash-Lite, a 68.5B-parameter sparse model with ~3B activated parameters, leveraging embedding scaling over expert scaling to achieve superior efficiency and performance in agentic and coding tasks, enhanced by system optimizations and speculative decoding.

Key Contributions

• We demonstrate that embedding scaling, particularly via N-gram embeddings, can outperform expert scaling in specific regimes, achieving a superior Pareto frontier by efficiently expanding parameter capacity without the routing overheads of MoE architectures.
• We systematically analyze architectural factors governing embedding scaling efficacy—including parameter budgeting, vocabulary sizing, initialization, and interactions with model width and depth—and identify N-gram embeddings as the most robust strategy across configurations.
• By integrating speculative decoding and custom system optimizations like N-gram caching and synchronized kernels, we convert embedding sparsity into measurable inference speedups, validated by LongCat-Flash-Lite, a 68.5B-parameter model with ~3B activated parameters that outperforms MoE baselines and excels in agentic and coding tasks.

Introduction

The authors leverage embedding scaling as an alternative to Mixture-of-Experts (MoE) for expanding sparse parameters in large language models, addressing the diminishing returns and system bottlenecks of expert scaling. Prior work has underexplored how embedding scaling compares to expert scaling in efficiency, how architectural choices like width, depth, and vocabulary size affect its performance, and how to optimize inference when embeddings are scaled. Their main contribution is a systematic framework that identifies regimes where embedding scaling outperforms expert scaling, characterizes key architectural tradeoffs, and introduces system-level optimizations—including speculative decoding and custom kernels—to convert sparse embedding gains into real-world speedups. They validate this with LongCat-Flash-Lite, a 68.5B-parameter model with 30B+ parameters in embeddings, which outperforms MoE baselines and competes with larger models, especially in agentic and coding tasks.

Method

The authors leverage a novel N-gram Embedding architecture to scale model parameters efficiently while maintaining computational and memory efficiency. This framework integrates a base embedding table with an expanded n-gram embedding branch, enabling vocabulary-free representation of token sequences. The base embedding branch uses a standard embedding table $E_0$E0​ to map individual tokens to embedding vectors. In parallel, the N-gram Embedding Branch processes sequences of tokens up to a maximum order $N$N, using hash functions to map n-grams to sub-tables. For each token $t_i$ti​, the augmented embedding $e_i$ei​ is computed as a weighted average of the base embedding and contributions from n-gram embeddings of orders 2 through $N$N. Each n-gram embedding is further decomposed into $K$K sub-tables, with each sub-table $E_{n,k}$En,k​ having a reduced dimensionality, and the outputs are projected back to the full embedding space using linear projection matrices $W_{n,k}$Wn,k​. This design ensures that the total parameter count remains invariant with respect to $N$N and $K$K, while enhancing the model's expressive capacity and reducing hash collisions.

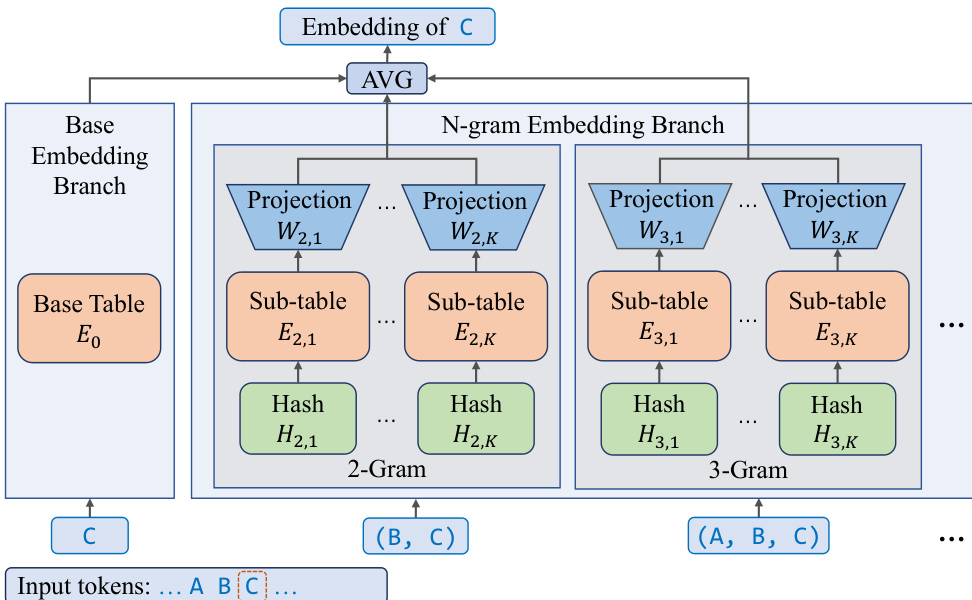
The N-gram Embedding mechanism redistributes parameters from the MoE layers to the embedding space, reducing the number of activated parameters during inference. This architectural shift is particularly beneficial in memory I/O-bound decoding scenarios, as it allows for larger effective batch sizes without increasing the computational load on the MoE layers. The increased embedding layer size does not penalize latency, as embedding lookups scale with the number of input tokens rather than the total number of parameters. To maximize hardware utilization, the model employs speculative decoding, which effectively expands the effective batch size and converts the theoretical advantage of parameter sparsity into tangible inference speedups.

To address the additional overhead introduced by N-gram Embedding, the authors introduce the $N$N-gram Cache, a specialized caching mechanism inspired by the KV cache. This cache manages N-gram IDs directly on the device using custom CUDA kernels, enabling low-overhead synchronization with inference optimization techniques. In speculative decoding scenarios, where the draft model operates with fewer layers and lower latency, the authors propose two complementary optimizations: using a conventional embedding layer for the draft model to bypass expensive n-gram lookups, and caching n-gram embeddings during the drafting phase to eliminate redundant computations in the verification step. These optimizations collectively reduce latency and improve throughput in speculative inference settings.

Beyond hardware efficiency, the authors explore synergies between N-gram Embedding and speculative decoding. The N-gram Embedding structure inherently encodes rich local context and token co-occurrence information, which can be leveraged to further accelerate inference. Two promising directions are identified: N-gram Embedding based drafting, where the N-gram embedding is repurposed as an ultra-fast draft model, and early rejection, where the N-gram Embedding representation serves as a semantic consistency check to prune low-probability draft tokens before verification. These strategies offer pathways to further optimize end-to-end latency.

Building upon the Per-Layer Embedding (PLE) approach, the authors propose Per-Layer N-gram Embedding (PLNE), which replaces the base embedding outputs with N-gram Embedding outputs at each layer. This extension enables more flexible and targeted parameter scaling within the MoE framework. The FFN output with PLNE is formalized as $\mathrm{FFN}^{(l)}(x_i) = W_d^{(l)} \big( \mathrm{SiLU}(W_\alpha^{(l)} x_i^{(l)}) \odot e_i^{(l)} \big)$FFN(l)(xi​)=Wd(l)​(SiLU(Wα(l)​xi(l)​)⊙ei(l)​), where $e_i^{(l)}$ei(l)​ is computed according to the N-gram Embedding formula with layer-specific embedding tables and projection matrices. This design allows for more granular control over parameter allocation and enhances the model's ability to capture local context.

Experiment

• Scaling N-gram Embedding outperforms expert scaling only when introduced beyond the “sweet spot” of expert count, with optimal gains at high sparsity levels (e.g., 1.3B activated parameters), achieving lower loss than MoE baselines at ratios up to 50.
• Allocating >50% of total parameters to N-gram Embedding degrades performance; optimal allocation caps at ~50%, aligning with a U-shaped loss curve observed in concurrent work.
• Vocabulary size for N-gram Embedding should avoid integer multiples of base vocabulary size to minimize hash collisions, especially critical for 2-gram hashing.
• N-gram order N=3–5 and sub-tables K≥2 yield near-optimal performance; minimal settings (N=2, K=1) underperform significantly.
• Embedding Amplification (via scaling factor √D or LayerNorm) reduces training loss by 0.02 across splits by preventing signal suppression from residual branches.
• Wider models (790M–1.3B activated parameters) extend the effective window for N-gram Embedding, preserving advantage even at high parameter ratios; deeper models (>20 layers) diminish its relative gain.
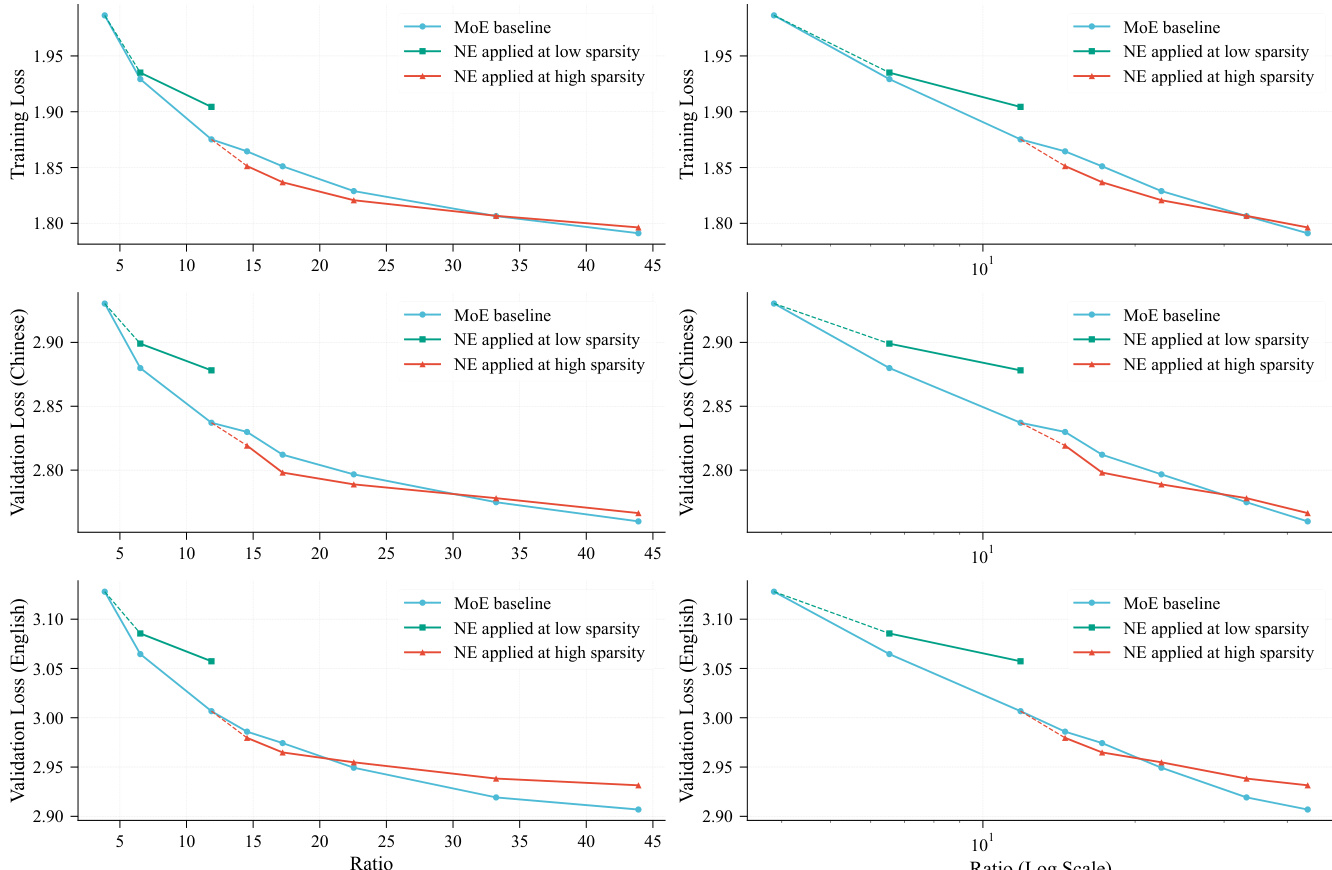
• LongCat-Flash-Lite (N-gram Embedding-enhanced) outperforms vanilla MoE baseline across MMLU, C-Eval, GSM8K, HumanEval+, and other benchmarks, validating embedding scaling efficacy.
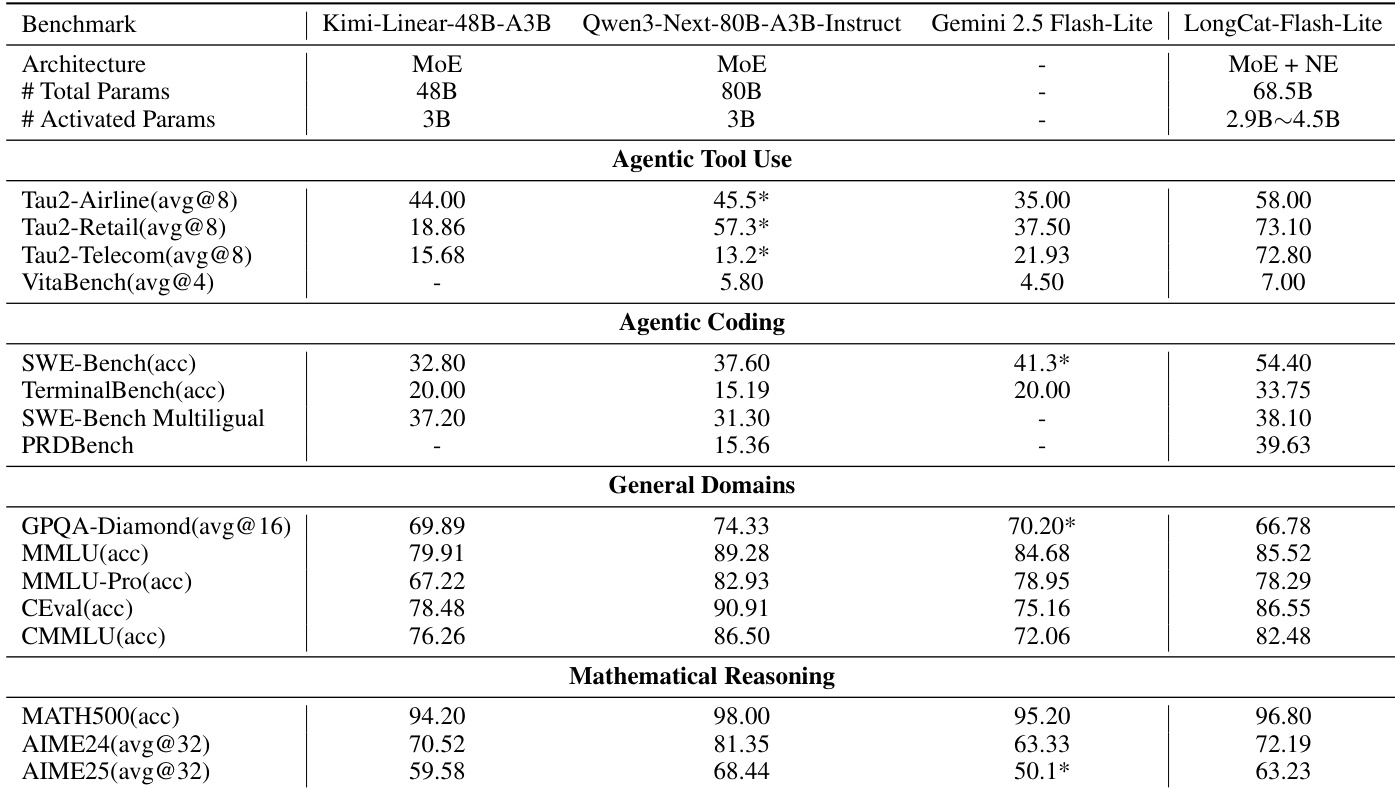
• LongCat-Flash-Lite excels in agentic tool use (τ²-Bench: 72.8–73.1; VitaBench: 7.00) and coding (SWE-Bench: 54.4; TerminalBench: 33.75), surpassing Qwen3-Next-80B, Gemini 2.5 Flash-Lite, and Kimi-Linear-48B-A3B.
• Achieves strong math reasoning (MATH500: 96.80; AIME24: 72.19) and general knowledge (MMLU: 85.52; CEval: 86.55), demonstrating broad capability with parameter efficiency.

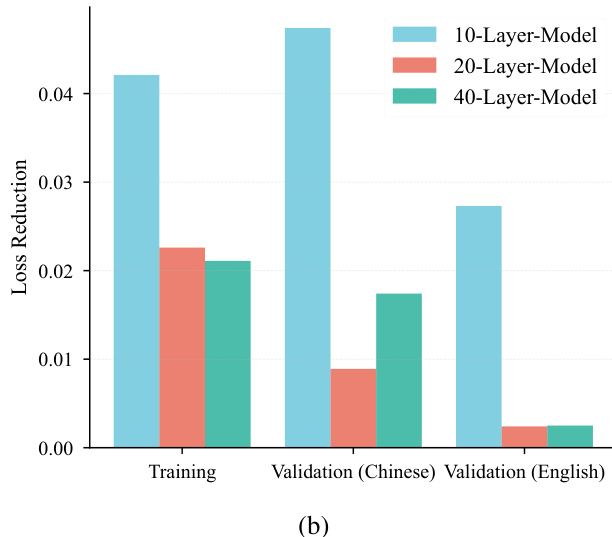
The authors use a bar chart to compare the loss reduction of models with different numbers of layers (10, 20, and 40) on training and validation tasks. Results show that the 10-layer model achieves the highest loss reduction on training and Chinese validation, while the 40-layer model performs best on English validation, indicating that deeper models may be more effective for certain validation tasks.

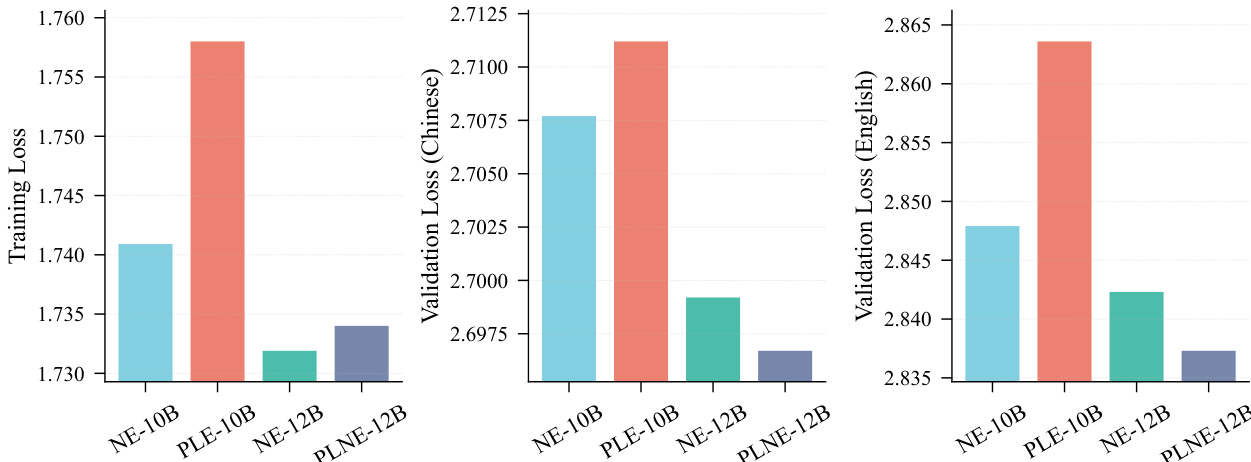
The authors compare the performance of different model variants on training and validation loss, showing that NE-10B achieves the lowest training loss and NE-12B achieves the lowest validation loss in both Chinese and English. The results indicate that increasing the model size from 10B to 12B parameters improves validation performance, with NE-12B outperforming PLE-10B and PLNE-12B across all metrics.

The authors compare LongCat-Flash-Lite-Vanilla and LongCat-Flash-Lite models on a range of benchmarks, showing that LongCat-Flash-Lite achieves higher scores than LongCat-Flash-Lite-Vanilla across most tasks in general, reasoning, and coding domains. This indicates that the proposed scaling approach with N-gram Embedding improves model performance over the baseline.

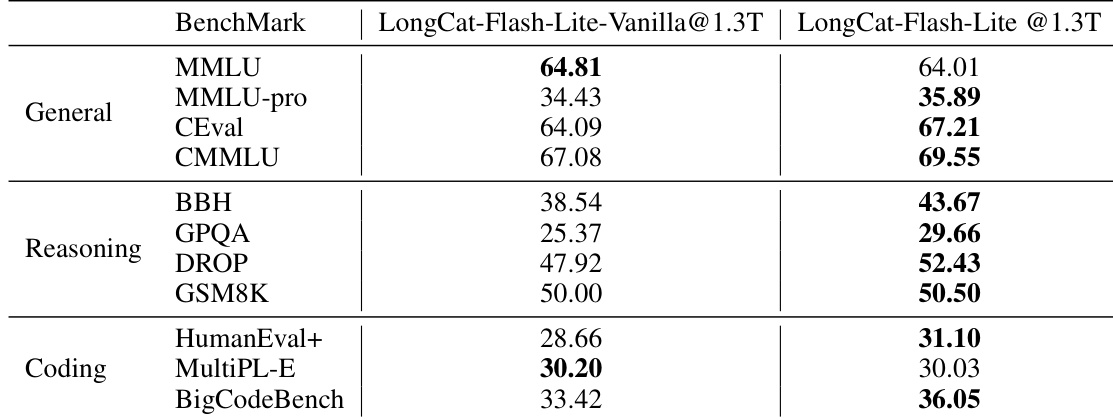
Results show that N-gram Embedding scaling outperforms expert scaling at high sparsity levels, with the performance advantage diminishing as the parameter ratio increases beyond a certain point. The optimal integration of N-gram Embedding occurs when the number of experts exceeds a threshold, and its benefits are more pronounced in wider models, while deeper models reduce its relative advantage.

The authors compare LongCat-Flash-Lite, which uses N-gram Embedding scaling, against several state-of-the-art models across multiple capability domains. Results show that LongCat-Flash-Lite achieves superior performance in agentic tool use and coding tasks, outperforming models like Qwen3-Next-80B-A3B-Instruct and Gemini 2.5 Flash-Lite, while maintaining competitive results in general knowledge and mathematical reasoning benchmarks. This indicates that scaling total parameters through N-gram Embedding effectively enhances model capabilities, particularly in practical, real-world applications.