Command Palette
Search for a command to run...
تأثير التفاحة السامة: التلاعب الاستراتيجي في الأسواق الوسيطة من خلال توسيع تقنية الوكلاء الذكية الذكية الاصطناعية
تأثير التفاحة السامة: التلاعب الاستراتيجي في الأسواق الوسيطة من خلال توسيع تقنية الوكلاء الذكية الذكية الاصطناعية
Eilam Shapira Roi Reichart Moshe Tennenholtz
الملخص
يُعد دمج الوكلاء الذكيين الاصطناعيين في الأسواق الاقتصادية تحوّلاً جوهرياً في نمط التفاعل الاستراتيجي. نستعرض الآثار الاقتصادية الناتجة عن توسيع مجموعة التقنيات المتاحة في ثلاث بيئات كلاسيكية من النماذج النظرية للألعاب: التفاوض (تقسيم الموارد)، والتفاوض (تداول المعلومات غير المتماثلة)، والإقناع (نقل المعلومات الاستراتيجية). نجد أن مجرد زيادة خيارات الوكلاء الذكية لا يكفي لتعديل توازن المكاسب والنتائج التنظيمية بشكل جذري، بل غالبًا ما يُولّد حوافز للجهات التنظيمية لتطوير ونشر تقنيات جديدة بشكل استباقي. وعلى النقيض من ذلك، نُحدّد ظاهرة استراتيجية تُسمّى تأثير "التفاحة المسمومة": حيث قد يُطلق وكيل تقنية جديدة لا يستخدمها هو ولا خصمه في النهاية، بل فقط لتمويه اختيار الجهاز التنظيمي لتصميم السوق لصالحه. ويؤدي هذا الإطلاق الاستراتيجي إلى تحسين مستوى رفاهية المُطلق على حساب الخصم، ويُضر بأهداف العدالة التي تسعى إليها الجهة التنظيمية. تُظهر نتائجنا أن الإطارات التنظيمية الثابتة عرضة للتحايل عبر توسيع نطاق التقنيات، مما يستدعي تصميم أسواق ديناميكية قادرة على التكيّف مع التغيرات المستمرة في القدرات الذكية الاصطناعية.
One-sentence Summary
The authors from Technion – Israel Institute of Technology propose that expanding AI agent technologies in economic markets induces strategic manipulation, exemplified by the "Poisoned Apple" effect, where agents release unused technologies to influence regulator decisions, undermining fairness and exposing limitations of static regulations, thus calling for adaptive, dynamic market designs.
Key Contributions
- The paper examines how expanding the set of available AI technologies in regulated markets disrupts equilibrium outcomes in three core economic settings—bargaining, negotiation, and persuasion—revealing that mere technological availability, even without adoption, can shift payoffs and regulatory decisions.
- It introduces the "Poisoned Apple" effect, a strategic phenomenon where an agent releases a technology they never use to manipulate the regulator’s choice of market design, thereby improving their own welfare at the expense of the opponent and fairness goals.
- The findings are grounded in game-theoretic models of sequential interaction, demonstrating that static regulatory frameworks are vulnerable to such manipulation, and thus call for dynamic market designs that adapt to the evolving strategy space of AI agents.
Introduction
The integration of AI agents into economic markets transforms strategic interactions, particularly in settings like bargaining, negotiation, and persuasion where technology choices influence outcomes. Prior work often assumes that expanding technological options is neutral or beneficial, but this research reveals a critical vulnerability: regulators using static market designs are susceptible to manipulation through strategic technology releases. The authors identify the "Poisoned Apple" effect, where an agent introduces a new AI technology not to use it, but to steer the regulator toward a market design that favors their payoff at the expense of their opponent and fairness goals. This phenomenon demonstrates that the mere availability of a technology can alter equilibria, undermining static regulatory frameworks. The authors’ key contribution is a formal meta-game model showing that regulatory designs must evolve dynamically to account for the expanding strategy space of AI agents, ensuring resilience against such manipulative behavior.
Dataset
- The dataset is derived from the GLEE (Games in Language-based Economic Environments) framework, which simulates strategic interactions among 13 state-of-the-art LLMs treated as economic agents across 1,320 distinct market configurations.
- It includes over 80,000 simulated games across three core game families: Bargaining (alternating-offers with surplus splitting), Negotiation (bilateral trade with private information), and Persuasion (sender-receiver with strategic information transmission).
- Each market is defined by three structural parameters: Information Structure (e.g., whether the seller knows the buyer’s valuation), Communication Form (e.g., binary signals vs. full-text persuasion), and Game Horizon (e.g., long-lived vs. myopic buyer behavior).
- The dataset captures strategic decisions from 13 LLMs, including proprietary models (e.g., GPT-4o, Claude 3.5/3.7 Sonnet, Gemini 1.5/2.0 series) and open-weight models (e.g., LLaMA 3.1-405B, LLaMA 3.3-70B, Mistral Large 2411), ensuring diverse reasoning capabilities and architectural designs.
- Payoffs are estimated using linear regression models trained on the full dataset, with one-hot encoded features for agent pairs, market configurations, and situational parameters. The final payoff estimates average over unknown situational variables, focusing on market and model pair effects.
- In the meta-game analysis, the authors use a training split based on the full GLEE dataset to compute equilibrium outcomes under varying technology sets. They begin with a baseline of N technologies (2 ≤ N < 13), identify the optimal market for a regulator’s objective (efficiency or fairness), then incrementally add one new technology at a time to study shifts in equilibrium and market selection.
- The authors apply a controlled expansion strategy: after adding a new technology, they recompute equilibria across all markets and re-optimize the regulator’s choice, isolating the causal impact of technology availability.
- No explicit cropping is applied; instead, the analysis relies on aggregated payoff matrices derived from the full simulation data, with metadata constructed from game family, market parameters, and model identities to support causal inference.
Method
The authors model the selection of AI delegates as a meta-game in which human principals, Alice and Bob, choose an AI agent from a set of available technologies. This framework is structured around a strategic interaction where the outcome depends on the interplay between agent payoffs and designer-defined metrics. For each market configuration, the authors construct four N×N matrices—where N is the number of available technologies—based on regression predictions. These matrices represent the row player payoff (UA), the column player payoff (UB), and two designer metrics: fairness (DF) and efficiency (DE). The game is defined by the interaction between Alice and Bob, with each selecting a technology, and the resulting payoffs determined by the corresponding entries in the payoff matrices.
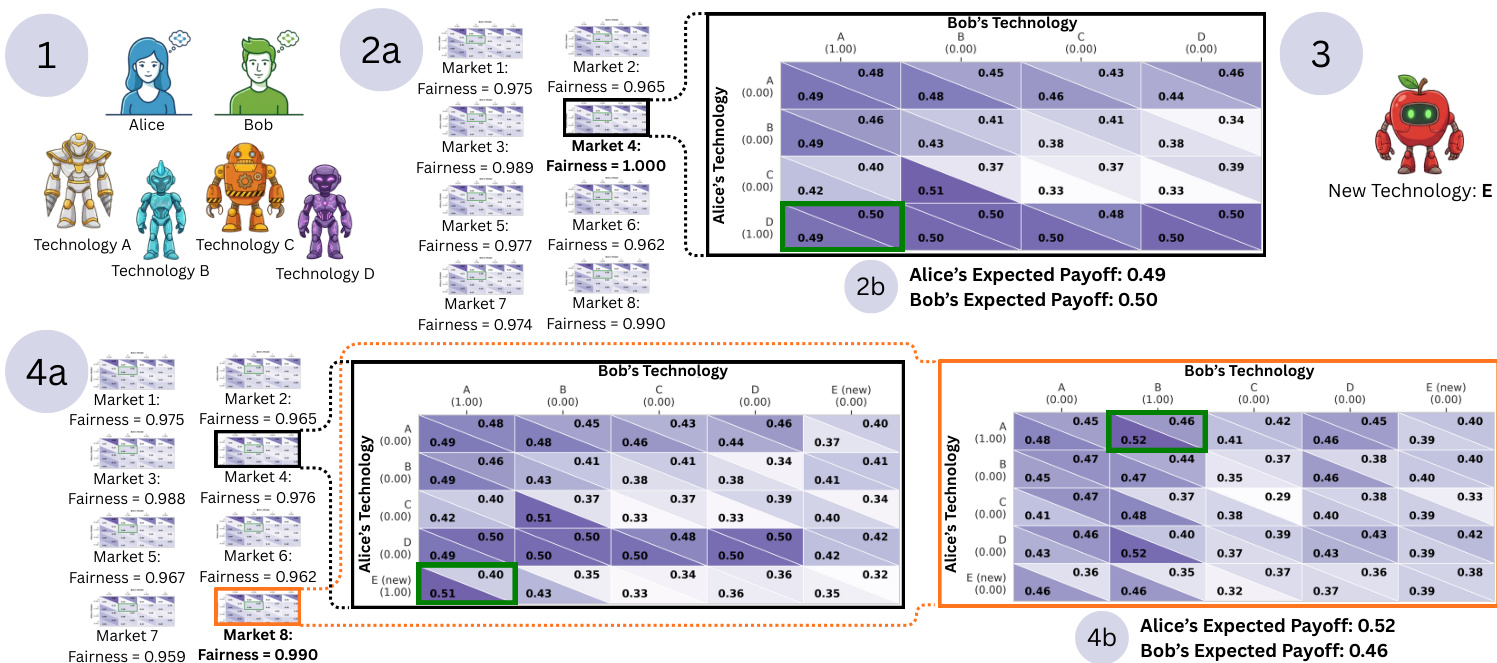
As shown in the figure below, the process begins with the initial setup where Alice and Bob are presented with a set of technologies (A, B, C, D), each associated with a specific market configuration. The framework evaluates the expected payoffs and fairness metrics across different market configurations. The authors compute the Mixed Strategy Nash Equilibrium (MSNE) for the game defined by UA and UB using the Lemke-Howson algorithm, implemented via the nashpy library. This algorithm identifies all equilibria for the game, and when multiple equilibria exist, the expected payoffs for the agents and the regulator are averaged across all such equilibria.
The regulatory optimization step follows, where the designer evaluates the expected value of the objective function VD(m) for each market m. This value is computed as:
VD(m)=(σA∗)T⋅Dm⋅σB∗where Dm is the designer matrix (either fairness or efficiency) for market m, and (σA∗,σB∗) is the computed equilibrium profile. The regulator then selects the market configuration m∗ that maximizes this expected value:
m∗=argm∈MmaxVD(m)This completes the meta-game loop, determining the final regulatory environment and the resulting agent payoffs. The framework enables the designer to optimize market structures based on desired social metrics, balancing agent incentives with broader policy goals.
Experiment
-
Poisoned Apple Effect: In a bargaining meta-game, Alice releases a new technology (Model E) not to use it, but to force the fairness-maximizing regulator to switch from Market 4 to Market 8. Despite Model E being unused in the new equilibrium, the market shift increases Alice’s payoff from 0.49 to 0.52 and decreases Bob’s from 0.50 to 0.46, demonstrating strategic manipulation via latent threat.
-
Systemic Vulnerability: Across 50,000 simulated meta-games, expanding the technology set caused payoff reversals in one-third of cases even when the new technology was not adopted, confirming that open-weight releases can enable regulatory arbitrage without actual deployment.
-
Regulatory Objectives and Stability: Technology expansion improves efficiency when the regulator optimizes for social welfare but often harms fairness. Regulatory metrics deteriorate in 40% of cases when market design is not updated post-release, highlighting the danger of regulatory inertia and the need for dynamic frameworks.
-
Core Results: On bargaining games, the Poisoned Apple effect led to a 0.03 increase in Alice’s payoff and a 0.04 decrease in Bob’s, despite no use of the new model, while fairness dropped from 1.000 to 0.976 in the original market—validating that strategic threat alone can reshape outcomes.
The authors use a bargaining game to demonstrate the "Poisoned Apple" effect, where Alice introduces a new technology (E) not to use it, but to force the regulator to change the market design. Results show that although the new technology is not adopted in the final equilibrium, the regulator's shift to a new market (Market 8) increases Alice's payoff from 0.49 to 0.52 while decreasing Bob's from 0.50 to 0.46, illustrating strategic manipulation through the threat of deployment.
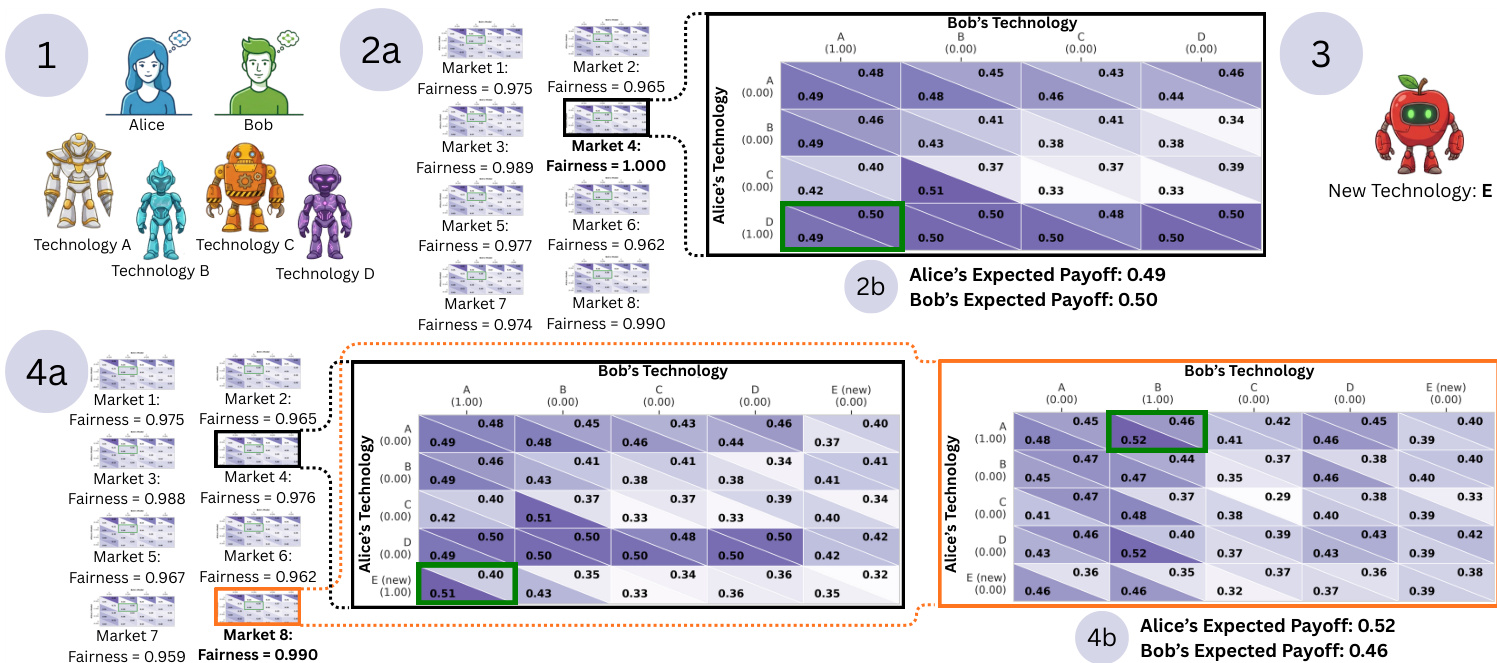
The authors use a bargaining game to demonstrate the "Poisoned Apple" effect, where Alice introduces a new technology (Model E) not to use it, but to force the regulator to change the market design. Results show that the regulator shifts from Market 4 (Fairness: 0.976) to Market 8 (Fairness: 0.990) to maintain fairness, even though the new technology is not adopted in the final equilibrium, leading to a payoff increase for Alice and a decrease for Bob.

The authors use a bargaining game to demonstrate the "Poisoned Apple" effect, where Alice introduces a new technology (Model E) not to use it, but to force the regulator to change the market design. Results show that the regulator shifts from Market 4, which had a fairness score of 1.000, to Market 8, which has a fairness score of 0.990, despite neither player using the new technology in the final equilibrium. This shift increases Alice's payoff from 0.49 to 0.52 while decreasing Bob's from 0.50 to 0.46, illustrating how strategic threats can manipulate regulatory outcomes without actual deployment.
