One-sentence Summary

The authors from the University of Pennsylvania and Microsoft Research propose Multiplex Thinking, a stochastic continuous reasoning framework that samples $K$K discrete tokens at each step, aggregates their embeddings into a single multiplex token, and enables on-policy reinforcement learning by preserving probabilistic semantics. Unlike deterministic continuous methods, it maintains sampling-based stochasticity for effective exploration, outperforming discrete CoT and RL baselines across math reasoning benchmarks with shorter, more efficient trajectories.

Key Contributions

• We propose Multiplex Thinking, a token-efficient reasoning framework that compresses multiple discrete reasoning candidates into a single continuous multiplex token through independent sampling, preserving stochasticity and enabling breadth-first exploration while reducing sequence length.

• The method formalizes a well-defined probability distribution over complete reasoning trajectories by factorizing the likelihood of sampled tokens, allowing direct reinforcement learning optimization over multiplex rollouts without the high cost of full discrete CoT generation.

• Empirical results show consistent improvements over discrete CoT and RL baselines across math reasoning benchmarks (Pass@1 to Pass@1024), achieving higher accuracy with shorter, more compact reasoning traces due to effective compression of high-entropy reasoning steps.

Introduction

Large language models (LLMs) have shown strong reasoning abilities, particularly in math and logic tasks, often through chain-of-thought (CoT) prompting that generates explicit intermediate steps. While reinforcement learning (RL) can further improve reasoning by optimizing over CoT rollouts, both approaches are costly due to the need for long, discrete token sequences—typically decoded in a depth-first manner that limits exploration. Existing continuous reasoning methods reduce token cost by encoding multiple paths in a single continuous token, but they are typically deterministic, collapsing the stochasticity essential for effective on-policy RL and exploration.

To address this, the authors propose Multiplex Thinking, a sampling-based continuous reasoning framework that retains stochasticity while enabling compact, efficient reasoning. At each step, it samples K discrete tokens from the model’s output distribution, maps them to embeddings, and aggregates them into a single multiplex token. This design preserves the probabilistic structure of discrete sampling, allows for rich, multi-path encoding during high-entropy reasoning, and enables direct RL optimization over entire rollouts via a factorized probability model.

The method achieves consistent improvements over discrete CoT and RL baselines across math benchmarks (Pass@1 to Pass@1024), with higher accuracy and shorter response lengths—demonstrating that stochastic continuous reasoning can bridge the gap between efficiency and effective exploration.

Dataset

• The dataset comprises multiple text sources, including web-crawled content, books, academic papers, and curated question-answer pairs, designed to support diverse reasoning and language tasks.
• It is divided into three main subsets:
  • Web Text: 1.2 billion tokens from publicly available web pages, filtered for readability and relevance using automated quality scoring and duplicate removal.
  • Book Corpus: 300 million tokens from digitized books, selected for linguistic diversity and factual accuracy, with content normalized for consistent formatting.
  • QA Pairs: 50 million tokens from expert-annotated question-answer datasets, including SQuAD, Natural Questions, and curated reasoning benchmarks, filtered to exclude low-quality or ambiguous entries.
• The authors use a mixture of these subsets during training, with dynamic sampling ratios adjusted per training phase: 60% web text, 30% book corpus, and 10% QA pairs in early stages, shifting to 50%, 40%, and 10% in later stages to emphasize factual consistency.
• All text is processed through a tokenization pipeline using a shared vocabulary, with sequences truncated or padded to a maximum length of 2048 tokens.
• A cropping strategy is applied to ensure balanced input length across batches, where longer sequences are randomly cropped to 2048 tokens, preserving semantic coherence.
• Metadata such as source type, domain category, and quality score are constructed during preprocessing and used to guide sampling and training dynamics.
• The training split follows a 90-5-5 ratio: 90% for training, 5% for validation, and 5% for testing, with no overlap between subsets.
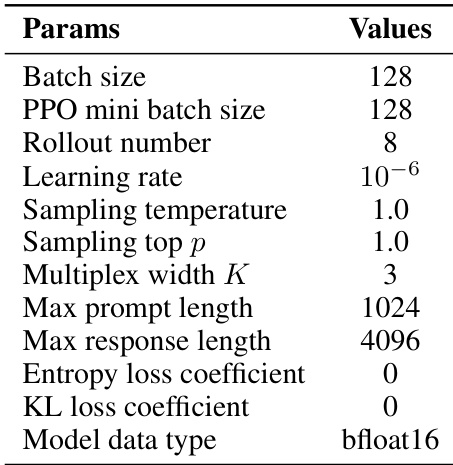
• Hyper-parameters for GRPO training, including learning rate, batch size, and entropy coefficient, are detailed in Table 6 and tuned to optimize convergence and performance across tasks.

Method

The authors leverage a novel reasoning paradigm called Multiplex Thinking, which integrates the information density of continuous representations with the probabilistic structure of discrete sampling. The framework operates in two primary phases: Branch and Merge. At each reasoning step, the model performs independent sampling, where $K$K discrete tokens are drawn from the language model's output distribution conditioned on the prompt and previous reasoning steps. These sampled tokens are then aggregated into a single continuous multiplex token through a weighted average of their embeddings. This aggregation process is designed to preserve the vocabulary embedding prior and maintain the sampling dynamics of standard discrete generation while enabling tractable optimization via reinforcement learning.

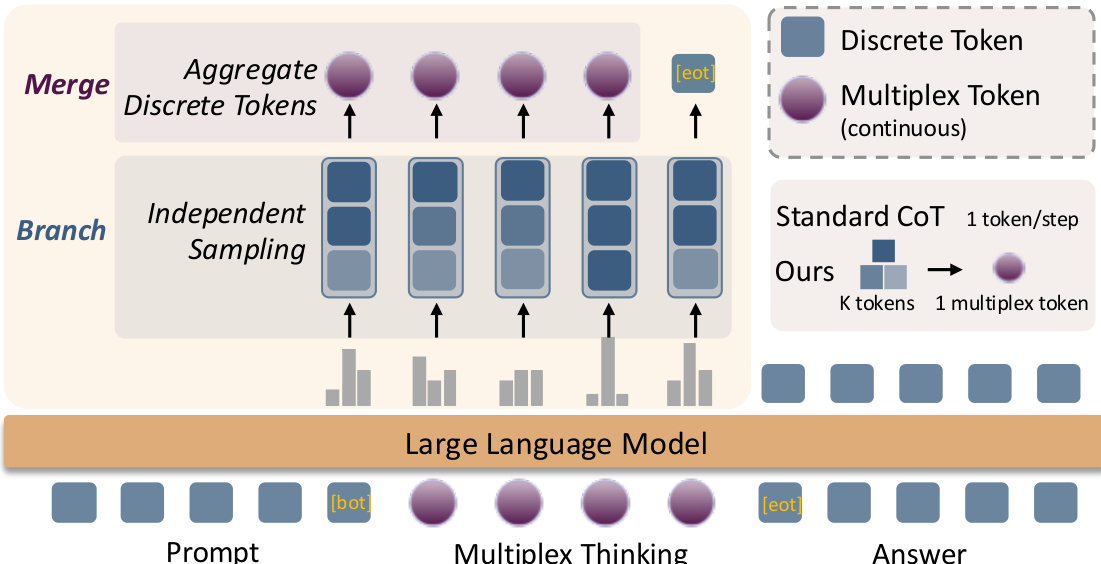
As shown in the figure below, the Branch phase involves sampling $K$K discrete tokens at each step, which are then passed to the Merge phase. In the Merge phase, these discrete tokens are aggregated into a continuous multiplex token using a weighting scheme that can be either uniform averaging or reweighting based on the model's language model head probabilities. The resulting multiplex token is then fed into the large language model as input for the next reasoning step. This process continues until the model generates a stop token, at which point the final answer is produced. The framework is designed to be self-adaptive: when the model is confident, the multiplex token behaves like a standard discrete token, and when uncertain, it compactly represents multiple plausible next steps without increasing sequence length. This design allows for efficient optimization of reasoning trajectories using on-policy reinforcement learning, as the probability of generating a multiplex token can be factorized into the sum of the log-probabilities of the constituent discrete samples.

Experiment

• Multiplex Thinking validates enhanced exploration capability through higher entropy in multiplex tokens, which scales linearly with multiplex width K, enabling exponential expansion of the effective search space from |V| to |V|^K, thereby maintaining probabilistic diversity in reasoning traces.
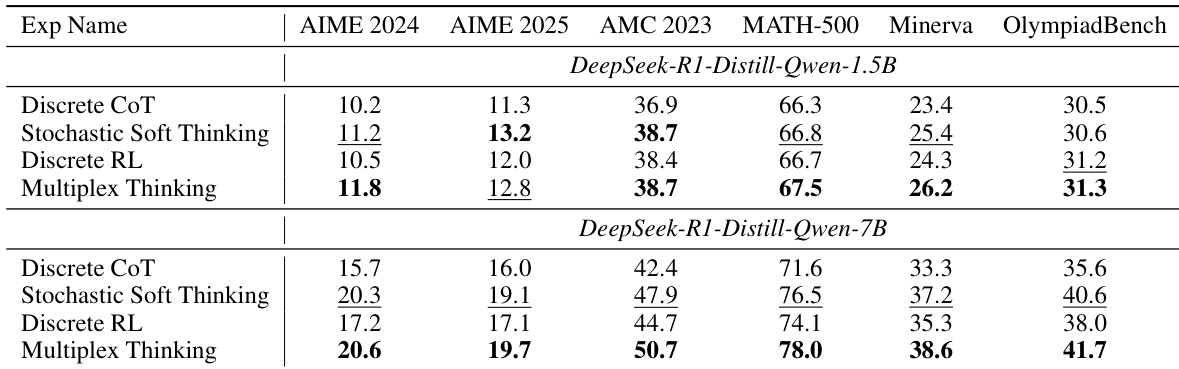
• On six mathematical reasoning benchmarks (AIME 2024, AIME 2025, AMC 2023, MATH-500, Minerva Math, OlympiadBench), Multiplex Thinking achieves the best Pass@1 accuracy in 11 out of 12 settings, surpassing Discrete CoT, Discrete RL, and Stochastic Soft Thinking baselines, with the 7B model showing dominant performance across all tasks.
• Multiplex Thinking exhibits superior test-time scaling, with Pass@1024 performance significantly outperforming discrete baselines—e.g., reaching ~55% on AIME 2025 (7B) compared to 40% for Discrete RL—demonstrating stronger exploration potential on hard, sparse-solution tasks.
• The method achieves higher accuracy with shorter response lengths: Multiplex Thinking-I with 4k tokens matches or exceeds Discrete CoT with 5k tokens, indicating higher information density and improved sample efficiency.
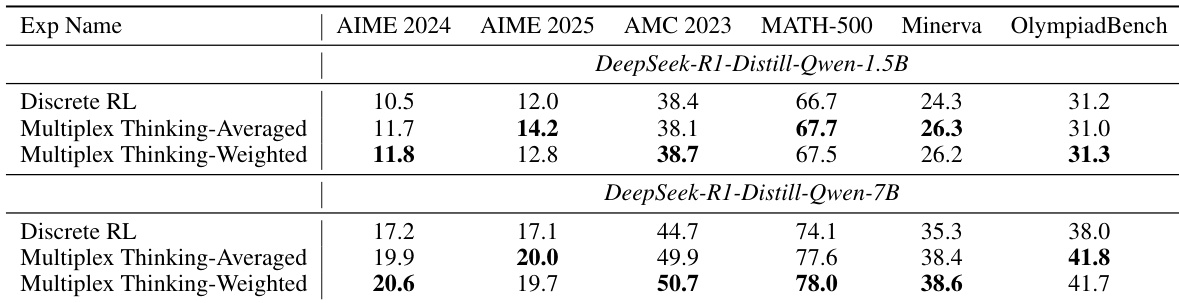
• Ablation studies confirm that multiplex representation provides intrinsic benefits: Multiplex Thinking-I (inference-only) outperforms Discrete CoT and is competitive with Stochastic Soft Thinking, while varying aggregation strategies (weighted vs. unweighted) yield similar performance, highlighting robustness to design choices.
• Entropy analysis shows lower policy entropy reduction during training for multiplex models, indicating sustained exploration and reduced premature commitment, which correlates with higher Pass@k upper bounds.
• Qualitative analysis reveals that Multiplex Thinking dynamically modulates exploration, preserving uncertainty at high-entropy decision points by compacting divergent candidates into multiplex tokens, enabling branching behavior at critical reasoning steps.

The authors analyze the entropy reduction during training for different multiplex widths, showing that multiplex training with $K=2$K=2 achieves the lowest entropy reduction of 5.82%, indicating more sustained exploration compared to the discrete RL baseline ($K=1$K=1) at 9.44%. As the multiplex width increases to $K=3$K=3 and $K=6$K=6, the entropy reduction rises to 6.03% and 7.09%, respectively, suggesting that larger widths lead to greater entropy collapse, though still less than the discrete baseline.

The authors compare the performance of Discrete CoT with different sequence lengths and Multiplex Thinking-I at a fixed 4k token budget. Results show that Multiplex Thinking-I-4k achieves a higher averaged accuracy of 40.5% compared to 39.6% for Discrete CoT-5k, demonstrating that multiplex tokens can achieve better performance with shorter sequences. This indicates that the increased information density of multiplex tokens allows for more efficient reasoning without requiring longer rollouts.

The authors compare the Pass@1 accuracy of Multiplex Thinking with Discrete RL across two model sizes and five datasets. Results show that Multiplex Thinking consistently outperforms Discrete RL, achieving the best performance in most settings, with the largest gains observed on the 7B model.

The authors use a multiplex width of $K=3$K=3 in their experiments, which is consistent with the optimal performance observed in their ablation study. This setting achieves a balance between exploration and efficiency, as increasing $K$K beyond 3 yields diminishing returns while maintaining higher information density per token compared to discrete baselines.

The authors use the table to compare the Pass@1 accuracy of Multiplex Thinking against Discrete CoT, Stochastic Soft Thinking, and Discrete RL across six mathematical reasoning benchmarks. Results show that Multiplex Thinking achieves the highest Pass@1 performance in 11 out of 12 experimental settings, consistently outperforming all baselines on both model sizes.