One-sentence Summary

The authors from Beihang University, UC Berkeley, Peking University, and Meituan propose HA-DW, a history-aware adaptive difficulty weighting method that corrects the inherent bias in group-relative advantage estimation within GRPO-based reinforcement learning from verifier rewards, improving exploration-exploitation balance and boosting performance across five mathematical reasoning benchmarks.

Key Contributions

• Group-based reinforcement learning from verifier rewards (RLVR) methods like GRPO rely on group-relative advantage estimation to avoid learned critics, but this approach suffers from an inherent bias that systematically underestimates advantages for hard prompts and overestimates them for easy prompts, leading to imbalanced exploration and exploitation.
• The authors propose History-Aware Adaptive Difficulty Weighting (HA-DW), a novel reweighting scheme that dynamically adjusts advantage estimates using an evolving difficulty anchor informed by long-term reward trends and historical training dynamics to correct this bias.
• Experiments on five mathematical reasoning benchmarks show that integrating HA-DW into GRPO and its variants consistently improves performance across model scales, even outperforming versions using more rollouts, demonstrating the critical impact of unbiased advantage estimation in RLVR.

Introduction

The authors investigate reinforcement learning from verifier rewards (RLVR), a key paradigm for post-training large language models on reasoning tasks, where group-based methods like GRPO dominate due to their simplicity and effectiveness. These methods estimate advantages within small groups of rollouts per prompt without requiring a separate critic, but prior work lacks a rigorous theoretical understanding of their underlying assumptions. The paper reveals a fundamental flaw: group-relative advantage estimation is systematically biased—underestimating true advantages for hard prompts and overestimating them for easy ones—leading to imbalanced exploration and exploitation that harms training stability and generalization. To address this, the authors propose History-Aware Adaptive Difficulty Weighting (HA-DW), a dynamic reweighting scheme that adjusts advantage estimates using an evolving difficulty anchor informed by long-term reward trends and historical training data. Theoretical analysis and experiments across five mathematical reasoning benchmarks show that HA-DW consistently improves performance when integrated into GRPO and its variants, even outperforming versions with more rollouts, demonstrating that correcting this bias is crucial for robust and efficient RLVR training.

Method

The proposed method, History-Aware Adaptive Difficulty Weighting (HA-DW), addresses the inherent bias in group-relative advantage estimation within reinforcement learning for language models. The framework operates in two primary phases: an evolving difficulty anchor that tracks the model's capability over time, and a history-aware reweighting mechanism that adjusts advantage estimates based on this evolving state. The overall architecture is designed to correct systematic underestimation for hard prompts and overestimation for easy prompts, which are common issues in group-relative policy optimization (GRPO) and its variants.

The core of the method is the evolving difficulty anchor, which models the model's solving capability as a latent belief state, denoted as $C_t$Ct​. This belief is updated across training batches using a Kalman-style filter. At each step $t$t, the observation $y_t$yt​, which is the batch-level accuracy (the ratio of correct responses), is used to update the prior belief $C_t^-$Ct−​ to the posterior belief $C_t^+$Ct+​. The update rule is $C_t^+ = (1 - \eta_t) C_t^- + \eta_t y_t$Ct+​=(1−ηt​)Ct−​+ηt​yt​, where $\eta_t$ηt​ is a dynamic forgetting factor. This factor is modulated by the model's stability, calculated as the standard deviation of the belief over the previous $m$m batches. A larger standard deviation, indicating high instability or rapid capability shifts, results in a higher $\eta_t$ηt​, allowing the model to adapt quickly. Conversely, a smaller standard deviation, indicating a stable model, results in a lower $\eta_t$ηt​, which preserves historical information and reduces noise. This evolving belief $C_t$Ct​ serves as a history-aware anchor for the subsequent difficulty-adaptive reweighting strategy.

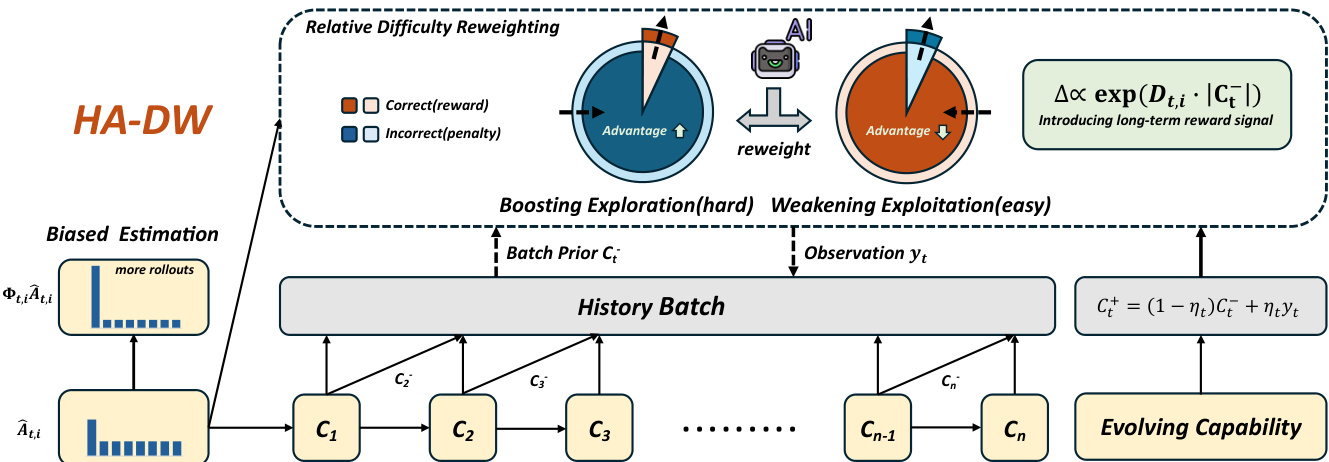
The second phase, history-aware adaptive difficulty weighting, uses the evolving difficulty anchor to correct the biased advantage estimates. The history-based prompt difficulty is defined as $diff_t^{his} = \hat{p}_t - C_t^-$diffthis​=p^​t​−Ct−​, where $\hat{p}_t$p^​t​ is the empirical group baseline. This value captures the deviation of the current prompt's difficulty from the model's current capability. The direction of the adjustment is determined by the sign of the product of the sign of the estimated advantage and the sign of the history-based difficulty, $D_{t,i} = - \text{sgn}(\hat{A}_{t,i}) \cdot \text{sgn}(diff_t^{his})$Dt,i​=−sgn(A^t,i​)⋅sgn(diffthis​). This ensures that the reweighting amplifies the advantage for difficult prompts (where $\hat{A}_{t,i}$A^t,i​ is likely underestimated) and suppresses it for easy prompts (where $\hat{A}_{t,i}$A^t,i​ is likely overestimated). The magnitude of the adjustment is quantified by the absolute history-based difficulty, $M_t = |diff_t^{his}|$Mt​=∣diffthis​∣. The final history-aware reweighting factor is defined as $\Phi_{t,i} = \lambda_{\text{scale}} \cdot \exp(D_{t,i} \cdot M_t)$Φt,i​=λscale​⋅exp(Dt,i​⋅Mt​), which is a smooth, multiplicative factor applied to the advantage term in the policy objective. This reweighted objective, $L_{\text{HA-DW}}(\theta)$LHA-DW​(θ), is then used for policy updates, effectively mitigating the bias identified in the theoretical analysis.

Experiment

• Evaluated HA-DW on Qwen3-4B-Base, Qwen3-8B-Base, and LLaMA-3.2-3B-Instruct across five RLVR benchmarks using GRPO, GSPO, and DAPO, demonstrating consistent performance gains over original group-relative methods.
• On MATH500, GRPO+HA-DW achieved 3.4% higher accuracy on Hard-level prompts compared to GRPO, validating improved exploration on challenging tasks.
• Training dynamics show HA-DW leads to higher accuracy plateaus and increased training rewards, with longer reasoning chains, indicating enhanced reasoning ability.
• Ablation on dynamic threshold $C_t$Ct​ confirms its superiority over fixed thresholds, with performance degradation when removed, highlighting its role in capturing long-term reward signals.
• Empirical analysis on MATH and DAPO-Math-17k reveals underestimation of correct responses at low rollouts (8), confirming biased advantage estimation on hard prompts.
• Theoretical analysis proves systematic bias in group-relative advantage estimation: overestimation for easy prompts ($p_t > 0.75$pt​>0.75) and underestimation for hard prompts ($p_t < 0.25$pt​<0.25), with bias probability exceeding 78% under $G \in [2,8]$G∈[2,8].
• Extension to non-binary rewards (Beta and truncated Gaussian) confirms similar bias patterns, with magnitude increasing as prompt difficulty deviates from 0.5.
• Ablation on group size $G$G shows HA-DW outperforms larger rollouts in low-sample settings, offering a computationally efficient alternative to scaling rollouts.
• Ablation on $\lambda_{\text{scale}}$λscale​ identifies optimal values (1.3–1.5) that balance adjustment across difficulty levels, maximizing performance.

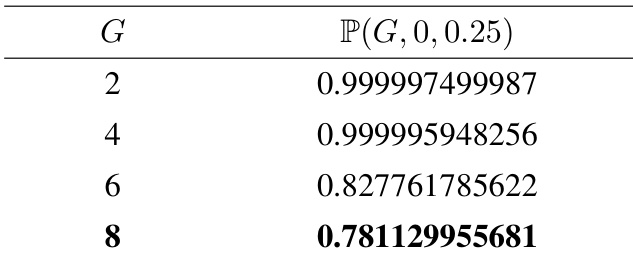
The authors use the table to quantify the probability of biased advantage estimation in group-relative reinforcement learning for hard prompts, showing that as the group size $G$G increases, the probability of overestimating the baseline decreases. Results show that for $G=2$G=2, the probability exceeds 0.999, but drops to 0.781 when $G=8$G=8, indicating that larger group sizes reduce the likelihood of bias.

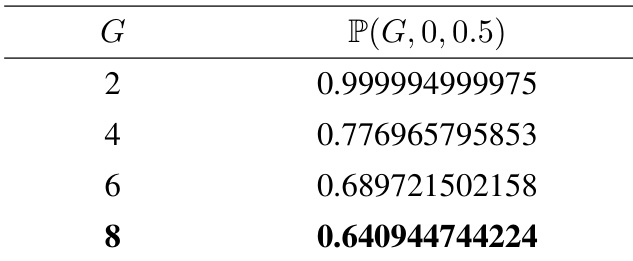
The authors use the table to analyze the probability of biased advantage estimation in group-relative reinforcement learning algorithms as the group size $G$G increases. Results show that the probability $\mathbb{P}(G, 0, 0.5)$P(G,0,0.5) decreases significantly with larger $G$G, indicating that the bias in advantage estimation becomes less likely as the group size grows.

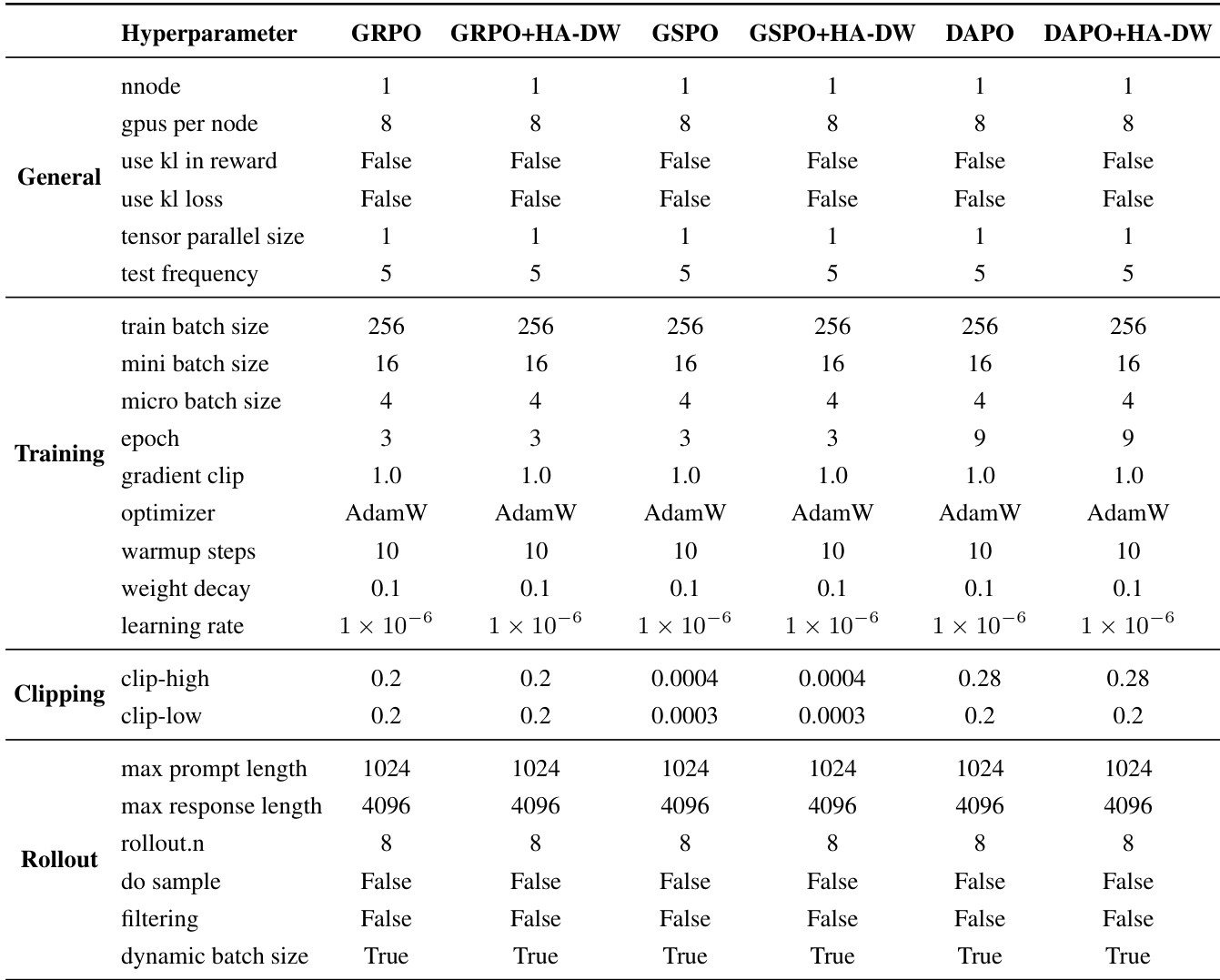
The authors use a consistent set of hyperparameters across all experiments, with the primary difference being the application of HA-DW to GRPO, GSPO, and DAPO. The table shows that the only modifications introduced by HA-DW are in the learning rate and clipping thresholds, while all other settings remain identical, ensuring a fair comparison.

The authors use the table to quantify the probability of biased advantage estimation in group-relative reinforcement learning algorithms, showing that as the group size $G$G increases, the probability of overestimating the advantage for hard prompts and underestimating it for easy prompts also increases. Results show that the bias becomes more pronounced with larger group sizes, with the probability reaching 0.781 for $G=6$G=6, indicating that larger groups exacerbate the estimation bias.

Results show that applying HA-DW to group-relative reinforcement learning algorithms improves performance across five benchmarks, with models trained using HA-DW achieving higher accuracy and rewards compared to the original methods. The training dynamics indicate that HA-DW enhances exploration on hard prompts and encourages longer reasoning chains, leading to better overall performance.