One-sentence Summary

The authors from Zhejiang University, Li Auto, and Shenzhen University propose InfiniDepth, a neural implicit field-based depth representation enabling arbitrary-resolution and fine-grained depth estimation, outperforming prior grid-based methods in both synthetic and real-world settings, with significant improvements in novel view synthesis under large viewpoint shifts.

Key Contributions

• InfiniDepth introduces a novel depth representation based on neural implicit fields, enabling continuous and localized depth queries at arbitrary 2D coordinates, which overcomes the resolution and detail limitations of traditional discrete grid-based depth estimation methods.
• The method achieves state-of-the-art performance on both synthetic and real-world benchmarks for relative and metric depth estimation, with significant improvements in fine-detail regions, as validated on the newly curated Synth4K 4K benchmark with high-frequency depth masks.
• InfiniDepth enhances novel view synthesis under large viewpoint shifts by introducing a depth query strategy that allocates sub-pixel budgets proportionally to surface elements, resulting in spatially uniform 3D point distributions and fewer holes and artifacts.

Introduction

The authors leverage neural implicit fields to represent depth, enabling continuous, arbitrary-resolution depth estimation—addressing a key limitation of prior methods that rely on discrete 2D grids. This grid-based approach restricts output resolution to training image dimensions and degrades fine geometric detail due to smoothing from upsampling or poor local modeling. InfiniDepth overcomes these issues with a lightweight, localized implicit decoder that queries depth at any continuous 2D coordinate using multi-scale features from a vision transformer, allowing precise, high-frequency detail recovery. The method also introduces a depth query strategy that allocates sub-pixel queries proportionally to surface area, producing spatially uniform 3D points and significantly improving novel view synthesis under large viewpoint shifts by reducing holes and artifacts. To rigorously evaluate high-resolution and fine-detail performance, the authors curate Synth4K, a 4K synthetic benchmark with diverse scenes and ground-truth depth, demonstrating state-of-the-art results across both relative and metric depth estimation tasks.

Dataset

• The dataset consists of Synth4K, a high-resolution synthetic benchmark curated from five video games: Cyberpunk 2077 (Synth4K-1), Marvel’s Spider-Man 2 (Synth4K-2), Miles Morales (Synth4K-3), Dead Island (Synth4K-4), and Watch Dogs (Synth4K-5).
• Each subset contains hundreds of 4K-resolution (3840×2160) RGB-D image pairs, capturing diverse indoor and outdoor environments with high-fidelity graphics and realistic lighting.
• Depth maps are extracted using ReShade, which accesses the game’s rendering pipeline to capture high-quality depth buffers during gameplay.
• To enable fine-grained evaluation, the authors construct a high-frequency (HF) mask by computing a multi-scale Laplacian energy map from the depth data.
• For each depth map, multiple smoothed versions are generated using Gaussian blurring at different scales, and the absolute Laplacian response is computed using a 4-neighborhood stencil.
• The final energy map is obtained by taking the per-pixel maximum across scales, normalized by the 98th percentile to reduce outlier influence.
• A temperature-based sharpening step adjusts the contrast of the energy map, with lower temperatures emphasizing sharp geometric details.
• Sampling probabilities for high-frequency pixels are derived from the sharpened energy map, and n candidate locations are selected via multinomial sampling.
• The HF mask is used to target evaluation on geometrically rich regions, enabling precise assessment of fine-grained depth estimation.
• For training, the model uses a mixture of datasets including MatrixCity, MVS-Synth, Blend-mvs, CREStereo, FSD, and DynamicReplica, in addition to those mentioned in the main paper.
• The training mixture is balanced using specific ratios to ensure robust generalization across diverse scenes and geometries.
• No image cropping is applied during training or evaluation; all data is used at native 4K resolution.
• Metadata such as scene type, game source, and depth resolution are preserved and used to guide data selection and analysis.

Method

The authors leverage a neural implicit field framework to represent depth as a continuous function of 2D image coordinates, conditioned on the input RGB image. This approach models depth estimation as $d_I(x, y) = N_\theta(I, (x, y))$dI​(x,y)=Nθ​(I,(x,y)), where $N_\theta$Nθ​ is a neural network that maps any continuous coordinate $(x, y)$(x,y) in the image plane to a depth value. The network is instantiated as a multi-scale local implicit decoder, which reassembles and aggregates features from multiple layers of a Vision Transformer (ViT) encoder to predict depth at arbitrary query points. The overall framework is illustrated in the diagram below.

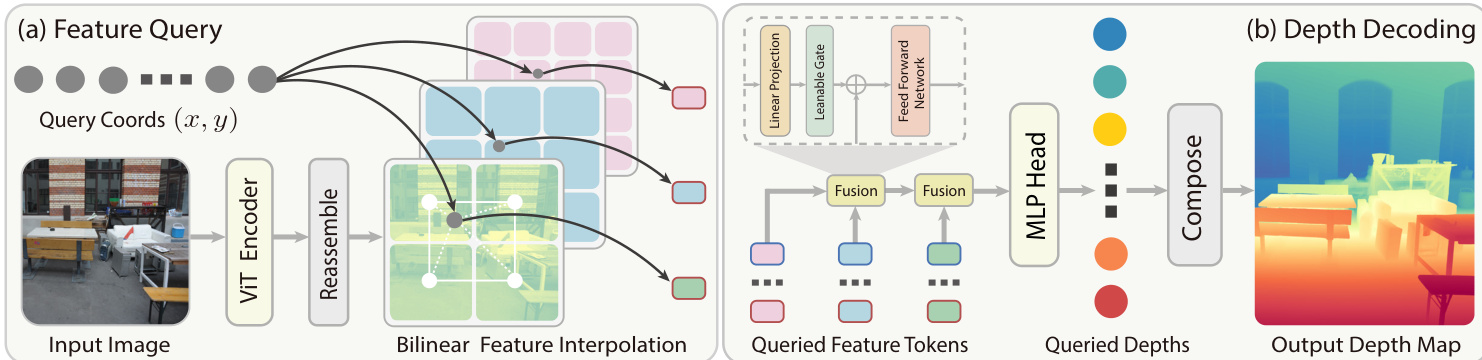
The decoder operates in two primary modules: Feature Query and Depth Decoding. In the Feature Query stage, the input image is encoded by a ViT to obtain a set of feature tokens. A reassemble block extracts tokens from multiple ViT layers and projects them to different hidden dimensions. Shallow-layer features are upsampled to higher spatial resolutions to capture fine local details, while deeper-layer features are retained at their native resolution to preserve global semantics. This process constructs a feature pyramid $\{f^k\}_{k=1}^L${fk}k=1L​, where $f^k \in \mathbb{R}^{h_k \times w_k \times C^k}$fk∈Rhk​×wk​×Ck. For a continuous query coordinate $(x, y)$(x,y), the corresponding location at each scale $k$k is computed as $(x_k, y_k) = (x \cdot w_k / W, y \cdot h_k / H)$(xk​,yk​)=(x⋅wk​/W,y⋅hk​/H). At each scale, a local grid neighborhood $\mathcal{N}_k(x_k, y_k)$Nk​(xk​,yk​) is defined, and features are aggregated using bilinear interpolation to yield a feature token $f_{(x, y)}^k$f(x,y)k​ for the query coordinate.

In the Depth Decoding stage, the multi-scale local descriptors $\{f_{(x,y)}^{k}\}_{k=1}^{L}${f(x,y)k​}k=1L​ are fused hierarchically from shallow to deep scales. The fusion begins with the shallowest feature $\mathbf{h}_1 := f_{(x,y)}^1$h1​:=f(x,y)1​. For each scale $k = 1, \ldots, L-1$k=1,…,L−1, a residual gated fusion block combines $\mathbf{h}_k$hk​ with the next-scale feature $f_{(x,y)}^{k+1}$f(x,y)k+1​, producing the fused feature $\mathbf{h}_{k+1}$hk+1​. This block is defined as $\mathbf{h}_{k+1} = \mathrm{FFN}_k \left( f_{(x,y)}^{k+1} + \mathbf{g}_k \odot \mathrm{Linear}(\mathbf{h}_k) \right)$hk+1​=FFNk​(f(x,y)k+1​+gk​⊙Linear(hk​)), where $\mathrm{Linear}(\cdot)$Linear(⋅) projects the feature dimension, $\mathbf{g}_k$gk​ is a learnable channel-wise gate, and $\odot$⊙ denotes element-wise multiplication. The FFN consists of a two-layer feed-forward network with non-linear activation. This hierarchical fusion process results in a final fused feature $\mathbf{h}_L$hL​ at the deepest scale, which is then passed through an MLP head to predict the depth value $d_I(x, y)$dI​(x,y).

The authors introduce an Infinite Depth Query strategy to address the density imbalance inherent in per-pixel depth prediction, which arises from perspective projection and surface orientation. The key insight is to allocate sub-pixel query budgets proportionally to each pixel's corresponding 3D surface area. The adaptive weight $w(x, y)$w(x,y) is derived as $w(x, y) = d_I(x, y)^2 / |\mathbf{n}(x, y) \cdot \mathbf{v}(x, y)| + \varepsilon$w(x,y)=dI​(x,y)2/∣n(x,y)⋅v(x,y)∣+ε, where $d_I(x, y)$dI​(x,y) is the queried depth, $\mathbf{n}(x, y)$n(x,y) is the surface normal, and $\mathbf{v}(x, y)$v(x,y) is the unit viewing direction. The surface normal is computed from the Jacobian of the back-projected 3D point $\mathbf{X}(x, y)$X(x,y) using the differentiable nature of the implicit depth field. The weight $w(x, y)$w(x,y) approximates the differential surface area $\Delta S(x, y)$ΔS(x,y), enabling the generation of uniformly distributed point clouds. The process of selecting sub-pixel query coordinates based on $w(x, y)$w(x,y) is detailed in the supplementary material.

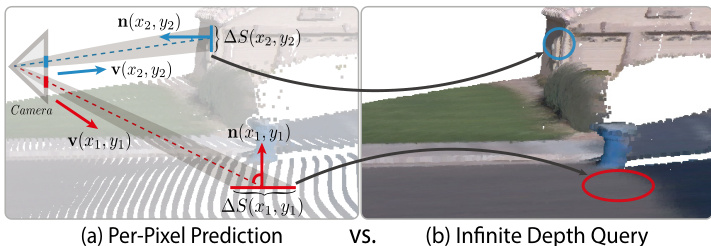
The uniform 3D point clouds generated by the Infinite Depth Query are then processed by a Gaussian Splatting (GS) Head. This head enriches each point with color and Plücker ray features extracted from the input image, combines them with ViT encoder features to form point-wise tokens, and processes each token through an MLP. The output is fed into multiple independent linear heads to predict Gaussian attributes, including position offsets, color offsets, scales, opacities, and rotations, enabling high-quality novel view synthesis. The training process involves depth normalization, where ground-truth depth values are converted to logarithmic space and then affine-invariant normalized. The InfiniDepth model is trained by sampling 100k coordinate-depth pairs per image from the original ground-truth depth map, and the GS head is trained with a learning rate of $1 \times 10^{-4}$1×10−4 using an $l1$l1 reconstruction loss and a perceptual LPIPS loss.

Experiment

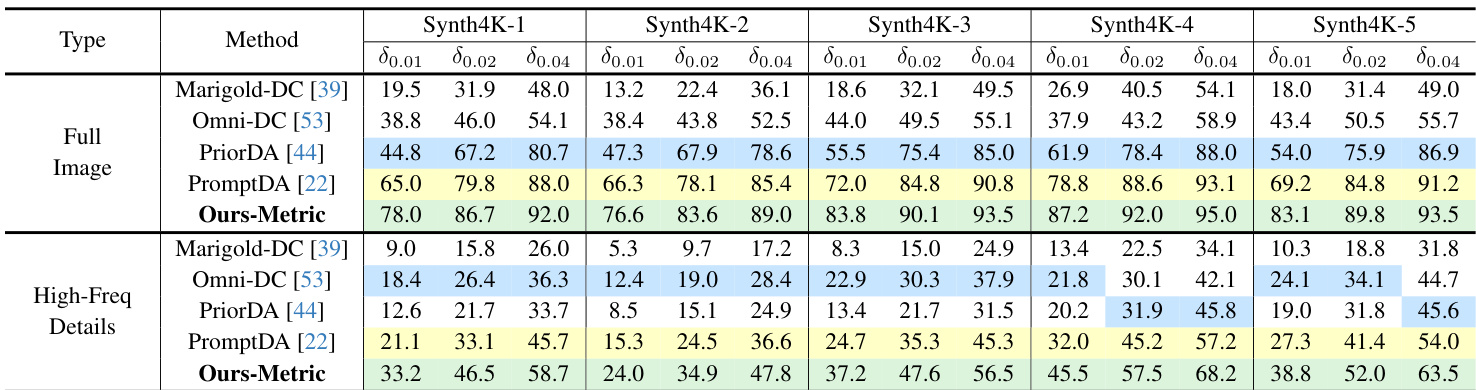
• Conducted zero-shot relative depth estimation on five real-world datasets (KITTI, ETH3D, NYUv2, ScanNet, DIODE) and Synth4K, achieving state-of-the-art performance on Synth4K with higher accuracy in $\delta_{0.5}$δ0.5​, $\delta_{1}$δ1​, and $\delta_{2}$δ2​ metrics, particularly excelling in full 4K-resolution and fine-detail prediction.
• Demonstrated effectiveness in metric depth estimation using sparse depth inputs (Ours-Metric), outperforming existing methods on both Synth4K and real-world datasets, with significant improvements in $\delta_{0.01}$δ0.01​, $\delta_{0.02}$δ0.02​, and $\delta_{0.04}$δ0.04​ accuracy.
• Ablation studies confirm that neural implicit depth representation significantly improves metric depth estimation and fine-grained detail recovery, while multi-scale feature query and bilinear interpolation in the implicit decoder yield optimal performance with minimal overhead.
• Achieved superior single-view novel view synthesis results under large viewpoint shifts by combining InfiniDepth with a lightweight Gaussian Splatting head, producing more complete and artifact-free reconstructions compared to ADGaussian.
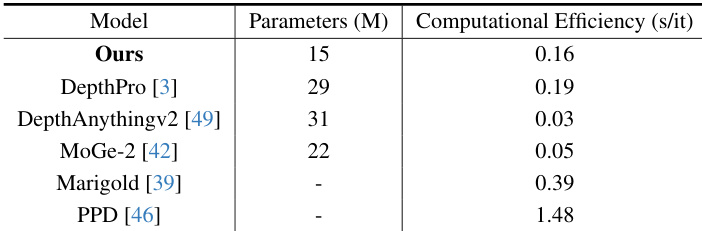
• Maintained computational efficiency with a lightweight decoder, outperforming other fine-grained depth methods in both speed and detail quality, despite slightly slower inference than some lightweight baselines.

The authors compare sub-pixel supervision with pixel-wise supervision for metric depth estimation, showing that sub-pixel supervision consistently improves performance across all datasets. Results indicate that sub-pixel supervision achieves higher accuracy, with the best improvement observed on DIODE (97.6 vs. 97.2) and Synth4K-4 (81.5 vs. 80.6).

The authors use a neural implicit field representation for depth estimation, and the results show that this approach significantly improves performance across all datasets compared to a baseline without implicit fields, particularly in high-resolution and fine-grained depth prediction. The full model achieves higher accuracy in both relative and metric depth estimation, with the most notable gains observed on Synth4K and real-world benchmarks.

The authors use a table to ablate the impact of neural implicit fields and multi-scale feature queries on depth estimation performance. Results show that the full model with neural implicit fields achieves the highest accuracy across all datasets, with the most significant improvements on Synth4K, while removing multi-scale query leads to a notable drop in performance, particularly on high-resolution data.

The authors compare the computational efficiency and parameter count of their method with several state-of-the-art depth estimation models. Results show that their model has the lowest parameter count among all compared methods, while achieving competitive computational efficiency, outperforming other fine-grained depth estimation approaches in both parameter efficiency and detail quality.

Results show that Ours-Metric achieves the highest performance across all metrics on both full-image and high-frequency detail regions of Synth4K, significantly outperforming all baselines in zero-shot relative and metric depth estimation. The method demonstrates superior accuracy and fine-grained detail recovery, particularly in high-frequency areas, highlighting its effectiveness for high-resolution depth prediction.