Command Palette
Search for a command to run...
DTS: تحسين النماذج الكبيرة للاستنتاج من خلال رسم مخططات شجرة التفكيك
DTS: تحسين النماذج الكبيرة للاستنتاج من خلال رسم مخططات شجرة التفكيك
Zicheng Xu Guanchu Wang Yu-Neng Chuang Guangyao Zheng Alexander S. Szalay Zirui Liu Vladimir Braverman
الملخص
تُظهر النماذج الكبيرة للاستدلال (LRMs) أداءً قوياً في المهام المعقدة التي تتطلب تفكيراً منطقياً، لكنها غالبًا ما تعاني من "التفكير المفرط"، ما يؤدي إلى إنتاج مسارات تفكير متسلسلة (CoT) طويلة جدًا، مما يزيد من تكاليف الاستدلال وربما يُضعف الدقة. تُظهر تحليلاتنا ارتباطاً عكسياً واضحاً بين طول عملية الاستدلال ودقتها، حيث تُحقّق المسارات القصيرة للاستدلال، في مختلف التفكيك العشوائي، أعلى مستويات الدقة باستمرار، بينما تُسجّل المسارات الأطول تراكمًا للأخطاء والتكرارات. يمكن العثور على هذه المسارات القصيرة المثلى بشكل مثالي من خلال استنفاد كامل لفضاء التفكير. ولكن فضاء التفكير المُرَتَّب على شكل شجرة ينمو بشكل أسي مع طول التسلسل، ما يجعل الاستكشاف الشامل مستحيلاً. لمعالجة هذه المشكلة، نقترح DTS، وهي إطار تفكيك مستقل عن النموذج، يُصوّر فضاء التفكير من خلال فتح فروع مختارة عند الرموز ذات الانتروبيا العالية، ويُطبّق توقّفًا مبكرًا لاختيار أقصر مسار مكتمل للاستدلال. يُعد هذا النهج تقريباً لحل مثالي يُحسّن من الكفاءة والدقة مع عدم الحاجة إلى تدريب إضافي أو إشراف. أظهرت التجارب على مجموعتي بيانات AIME2024 وAIME2025 باستخدام نموذج DeepSeek-R1-Distill-Qwen-7B و1.5B أن DTS يُحسّن الدقة بنسبة تصل إلى 8%، ويقلل من طول المسار المتوسط للاستدلال بنسبة 23%، ويقلل من تكرار العناصر بنسبة 12%، ما يُثبت قدرة DTS على تحسين استدلال النماذج الكبيرة للتفكير بفعالية وقابلية للتوسع.
Summarization
Researchers from Rice University, University of Minnesota, and Johns Hopkins University propose DTS, a model-agnostic decoding framework that reduces overthinking in Large Reasoning Models by selectively exploring high-entropy decision points and prioritizing shorter reasoning paths. DTS improves accuracy by up to 8% and cuts reasoning length by 23% without retraining, enabling more efficient and accurate AI reasoning on complex tasks.
Key Contributions
- DTS introduces a training-free, model-agnostic decoding framework that reduces overthinking in Large Reasoning Models by selectively exploring high-entropy decision points in the reasoning process.
- It constructs a compact decoding tree using parallel auto-regressive generation and applies early stopping to identify the shortest complete and accurate reasoning path.
- Experiments show DTS improves accuracy by up to 8%, reduces average reasoning length by 23%, and decreases repetition frequency by 12% on AIME2024 and AIME2025 benchmarks.
Introduction
Large Reasoning Models (LRMs) excel at complex tasks by generating step-by-step chain-of-thought (CoT) reasoning, but they often suffer from overthinking—producing long, redundant reasoning paths that increase inference cost and hurt accuracy. Prior work has attempted to address this through training-based methods like supervised fine-tuning or reinforcement learning on compressed or length-penalized data, or via adaptive pruning mechanisms. However, these approaches require additional labeled data and training, limiting scalability, while train-free methods often lack consistent performance gains.
The authors leverage the observation that shorter reasoning paths are empirically more accurate, forming a tree-structured reasoning space during autoregressive generation where optimal paths are short but buried in an exponentially large search space. To efficiently approximate the best path without training, they propose DTS (Decoding Tree Sketching), a model-agnostic decoding framework that dynamically constructs a compact reasoning tree at inference time.
- Uses next-token entropy to selectively branch only at high-uncertainty tokens, reducing search complexity.
- Applies early stopping to return the shortest completed reasoning path, aligning with the observed accuracy-length anti-correlation.
- Operates entirely at decoding time with GPU parallelism, enabling training-free, plug-and-play deployment across models.
Method
The authors leverage a novel decoding strategy called Decoding Tree Sketching (DTS) to efficiently identify the shortest reasoning path in Large Reasoning Models (LRMs), capitalizing on the observed anti-correlation between reasoning length and accuracy. Rather than exhaustively exploring the exponentially growing space of all possible reasoning sequences, DTS constructs a pruned decoding tree that selectively expands branches only at high-uncertainty tokens, thereby approximating the optimal short path while maintaining computational feasibility.
The core mechanism of DTS hinges on an adaptive branch function F(x,ξ) that determines whether to generate a single token or spawn multiple branches at each decoding step. This decision is governed by the entropy H(v) of the next-token distribution P(v)=f(x,ξ), where f denotes the LRM. When H(v)≥τ, indicating high uncertainty, DTS selects the top-K most probable tokens to initiate new branches; otherwise, it samples a single token. Formally:
F(x,ξ)={{v1,…,vK∣pv1,…,pvK≥p~K}{v1}, v1∼P(v)if H(v)≥τ,if H(v)<τ,where p~K is the K-th largest probability in P(v). This entropy-based gating allows DTS to focus computational resources on regions of the reasoning space where the model is uncertain, while proceeding deterministically in confident regions.
As shown in the figure below, the decoding tree grows in a breadth-first manner, with each node representing a token and edges denoting transitions. Branching occurs only at steps t1 and t2, where entropy exceeds the threshold τ, and the top two tokens are selected for expansion. Low-entropy steps proceed linearly, preserving efficiency.
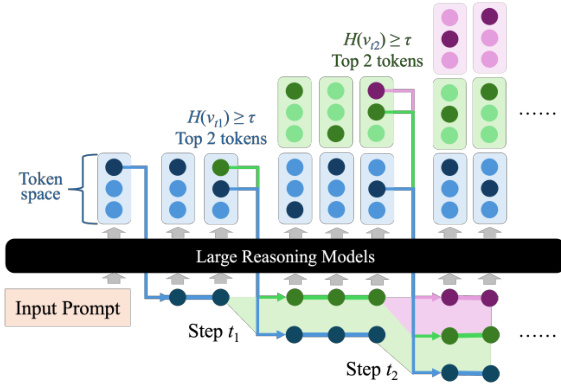
At each time step t, DTS maintains a set of active reasoning sequences Tt, initialized as T0=∅. For each sequence ξ∈Tt, the model applies F(x,ξ) to generate next tokens, which are appended to form new sequences. The set is then updated as:
Tt+1={ξ⊕vi∣vi∈F(x,ξ), ξ∈Tt}.This process continues iteratively, with all branches generated in parallel to exploit GPU acceleration, ensuring scalability.
Early termination is triggered as soon as any branch emits the ending token ⟨e⟩, following the principle that shorter reasoning paths yield higher accuracy. Formally, DTS stops at step t if ⋁ξ∈Tt1[⟨e⟩∈ξ], and returns the first completed sequence as the final output.
An illustrative example is shown in the figure below, where DTS processes the prompt “What’s the area of a rectangle with length 12 and width 9?”. Branching occurs at steps t1 and t2, generating multiple reasoning paths. The purple branch terminates first with the correct answer “area= 12×9=108”, which is returned as the final output.
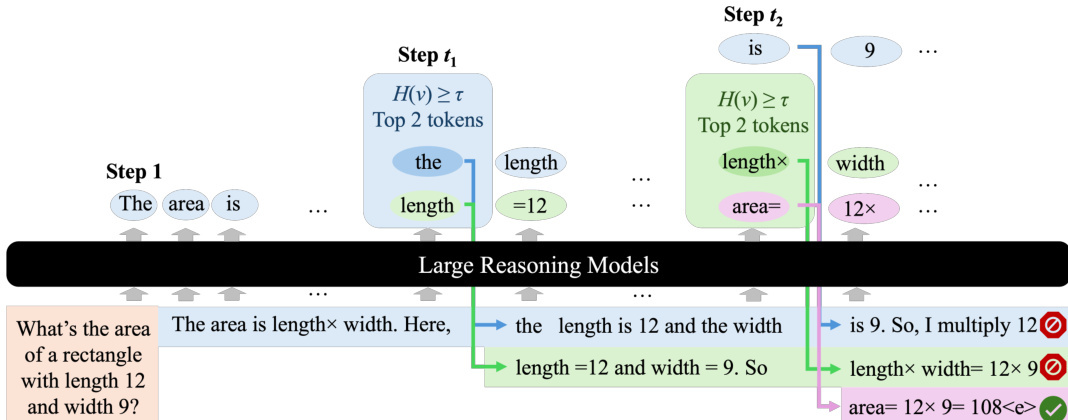
The algorithm follows a breadth-first search over the sketched tree, guaranteeing that the shortest valid reasoning path is identified. All active branches are expanded in parallel, enabling efficient and scalable inference without sacrificing the quality of the reasoning output.
Experiment
Respond strictly in English.
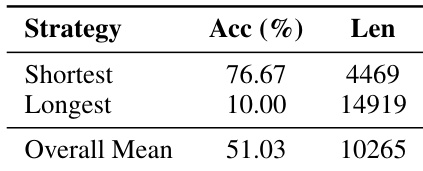
The authors use 100 stochastic decodes per AIME24 problem to evaluate reasoning trajectories, finding that selecting the shortest response yields 76.67% accuracy with significantly fewer tokens than the longest or mean responses. Results show a strong anti-correlation between response length and accuracy, indicating that verbose reasoning degrades performance. This supports the motivation for DTS, which prioritizes shorter, more efficient reasoning paths to improve both accuracy and efficiency.
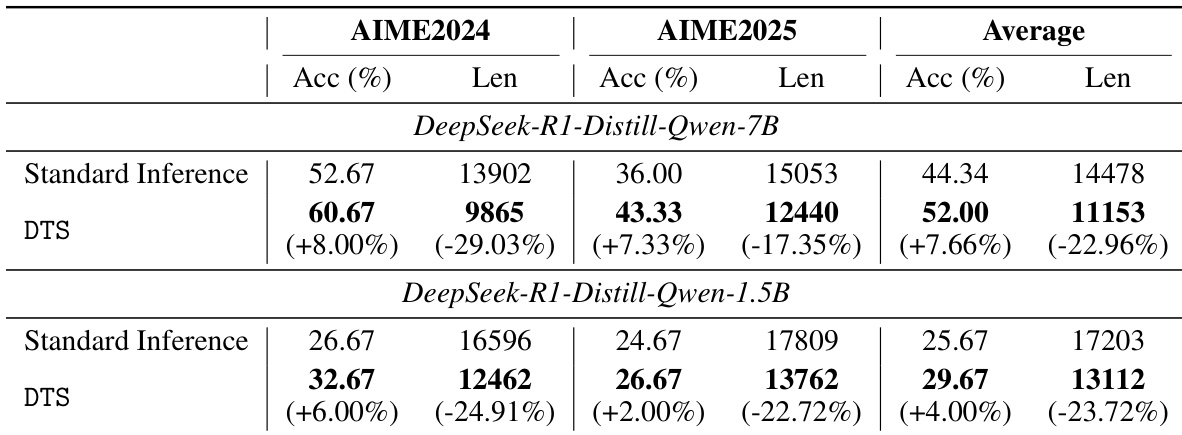
The authors use the DTS framework to improve reasoning performance and efficiency for DeepSeek-R1-Distill-Qwen models on AIME2024 and AIME2025. Results show DTS consistently increases accuracy by 4% to 8% while reducing response length by 17% to 29% compared to standard inference, with the 7B model achieving a 7.66% average accuracy gain and 22.96% length reduction. These improvements hold across both model sizes and datasets, demonstrating DTS’s effectiveness in balancing performance and efficiency without training.
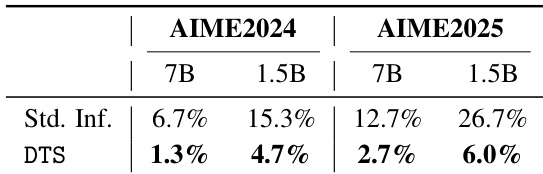
The authors use DTS to reduce endless repetition in reasoning trajectories, showing that it lowers repetition rates across both AIME2024 and AIME2025 benchmarks for 7B and 1.5B models. Results show DTS cuts repetition from 6.7% to 1.3% on AIME2024 for the 7B model and from 26.7% to 6.0% on AIME2025 for the 1.5B model. This confirms DTS effectively prunes repetitive paths by favoring shorter, completed reasoning traces.