Command Palette
Search for a command to run...
流体圧力を考慮したコイナ地震の非線形動的応答解析
チュートリアルの紹介
Abaqus の紹介
Abaqus は、エンジニアリング シミュレーションの分野で広く使用されている強力な有限要素解析 (FEA) ソフトウェアです。有限要素法を通じてさまざまな工学上の問題をシミュレートおよび分析し、単純な線形問題から複雑な非線形問題に至るまでの問題を処理できます。 Abaqus はもともと 1978 年にリリースされ、Hibbitt, Karlsson & Sorensen, Inc. (HKS) によって開発されました。その後、ABAQUS に名前が変更され、2005 年に Dassault Systèmes に買収されました。
チュートリアルの紹介
このチュートリアルは公式の Abaqus チュートリアルです。重力式コンクリートダムの地震解析。この例では、任意の荷重を受けるコンクリート構造物の安定性と損傷を評価するための、コンクリートの損傷塑性材料モデルの一般的な適用方法を示します。
このチュートリアルでは、1967 年 12 月 11 日にマグニチュード 6.5 の地震に見舞われたコイナ ダムを分析します。この問題が選ばれたのは、Chopra と Chakrabarti (1973)、Bhattacharjee と Léger (1993)、Ghrib と Tinawi (1995)、Cervera らを含む多くの研究者によって広範囲に分析されているためです。 (1996年)、LeeとFenves(1998年)を参照。
基本パラメータの紹介
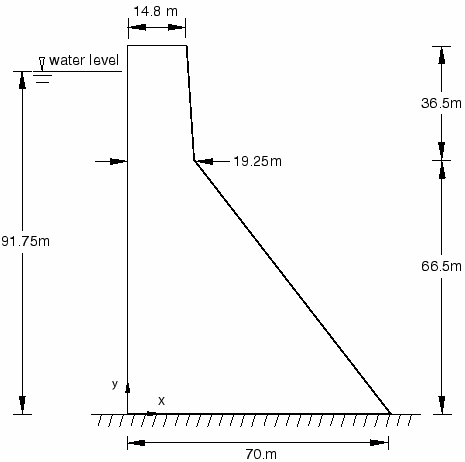
コイナダムの典型的な非越流部の断面形状を図 1 に示します。このダム部は高さ 103 メートル、底部の幅は 71 メートルです。ダム断面の上流面は垂直であると仮定されます。地震発生時の貯水池の水深はhわ=91.75メートル。研究者らによると、平面応力条件下での非越流ダム部分の2次元解析が検討された。
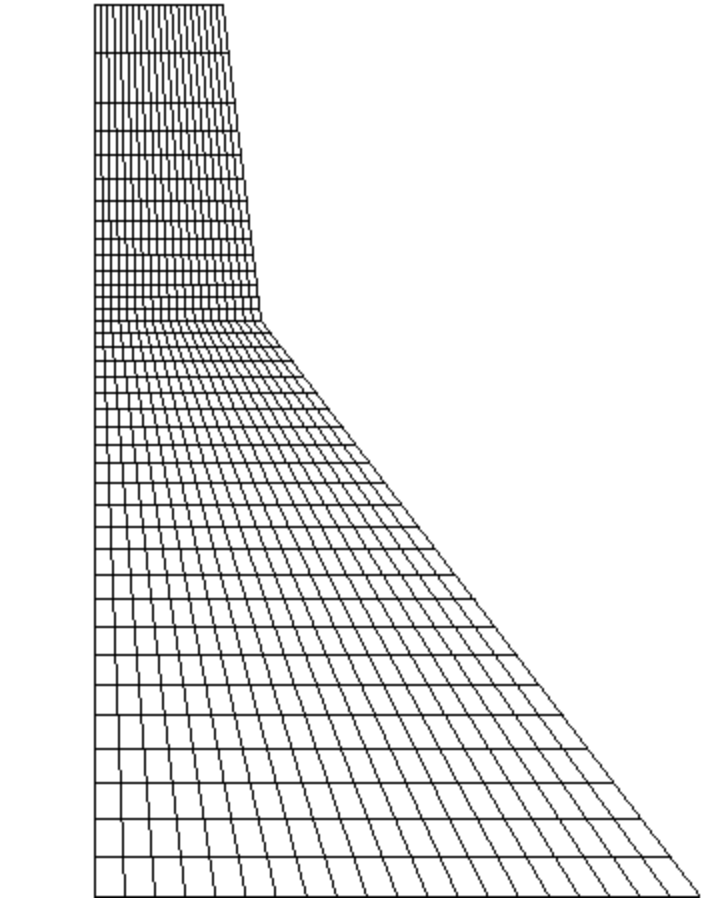
解析に使用した有限要素メッシュを図 2 に示します。メッシュは 760 個の 1 次、低積分、平面応力要素 (CPS4R) で構成されています。ノードは、ダムの左下隅を中心としたグローバル直交座標系で定義され、垂直の y 軸は上向き、水平の x 軸は下流向きになります。

この例では、基礎が剛性であると仮定して、ダムと基礎間の相互作用を無視します。地震動の横方向成分によるダムと貯水池の間の動的相互作用は、ウェスターガード付加質量法によって単純な形でモデル化できます。ウェスターガード (1933) によれば、地震の際にダムに水が及ぼす流体力学的圧力は、一定量の水がダムとともに前後に移動するのと同等であり、貯水池の残りの部分は静止したままである。上流表面の単位面積あたりの追加質量は、近似式で表すことができます。 (ただし、y≤h)わ、ρわ=1000kg/m3 水の密度です。 Abaqus/Standard 解析では、追加質量法は、ユーザー サブルーチン UEL でコード化された単純な 2 ノード ユーザー要素によって実装されます。地面の動きの垂直成分によって生成される流体圧力は小さいと考えられるため、すべてのシミュレーションで無視されます。
(ただし、y≤h)わ、ρわ=1000kg/m3 水の密度です。 Abaqus/Standard 解析では、追加質量法は、ユーザー サブルーチン UEL でコード化された単純な 2 ノード ユーザー要素によって実装されます。地面の動きの垂直成分によって生成される流体圧力は小さいと考えられるため、すべてのシミュレーションで無視されます。
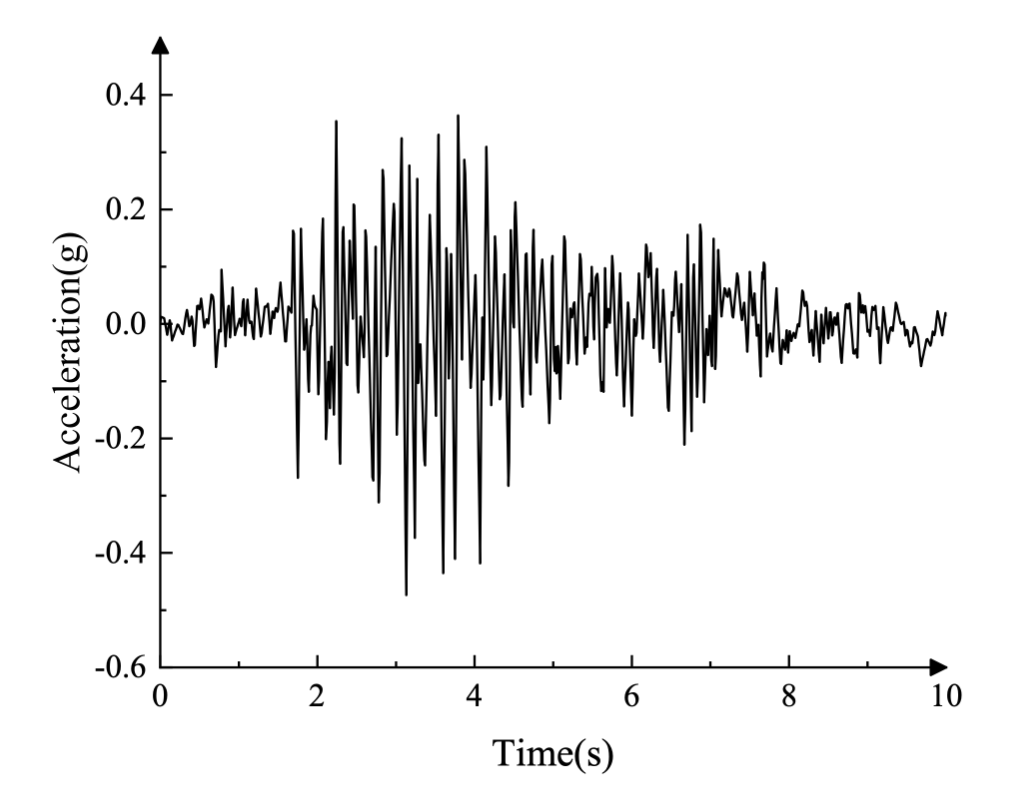
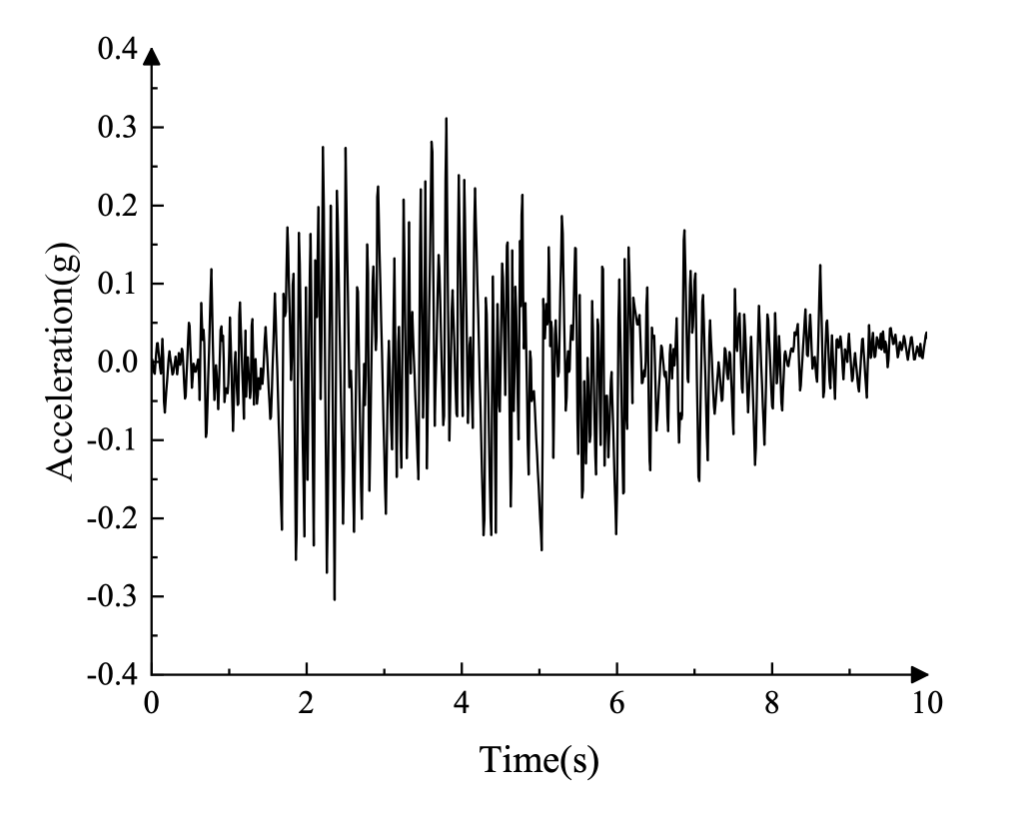
コイナ地震中に記録された地面加速度の横方向および垂直方向の成分を図 3 に示します (g = 9.81 m/s²)。地震励起の前に、ダムは自身の重量によって発生する重力荷重と上流面の貯水池によって発生する静水圧を受けます。
コンクリート材料の機械的挙動は、コンクリート損傷塑性構成モデルによってシミュレートされます。シミュレーションに使用した材料特性を表1と図4に示します。これらの特性は、コイナダムのコンクリート材料の代表的なものと考えられており、以前の研究者によって使用された特性に基づいています。これらの材料特性を取得するにあたり、いくつかの仮定が立てられました。特に注目すべきは、コンクリートの引張挙動の較正です。引張強度は極限圧縮強度σとして推定される。cu = 10% は 24.1 MPa であり、速度効果を考慮するために動的拡大係数 1.2 を乗じたものである。したがって、σt0 = 2.9 MPa。構造の補強不足によりメッシュ感度から不適切な結果が生じるのを避けるために、図 4.1 に示すように、応力-ひずみ曲線ではなく応力/変位曲線を指定して引張破損後の挙動を指定します。これは、亀裂後の応力/変位曲線を通じて実現されます。
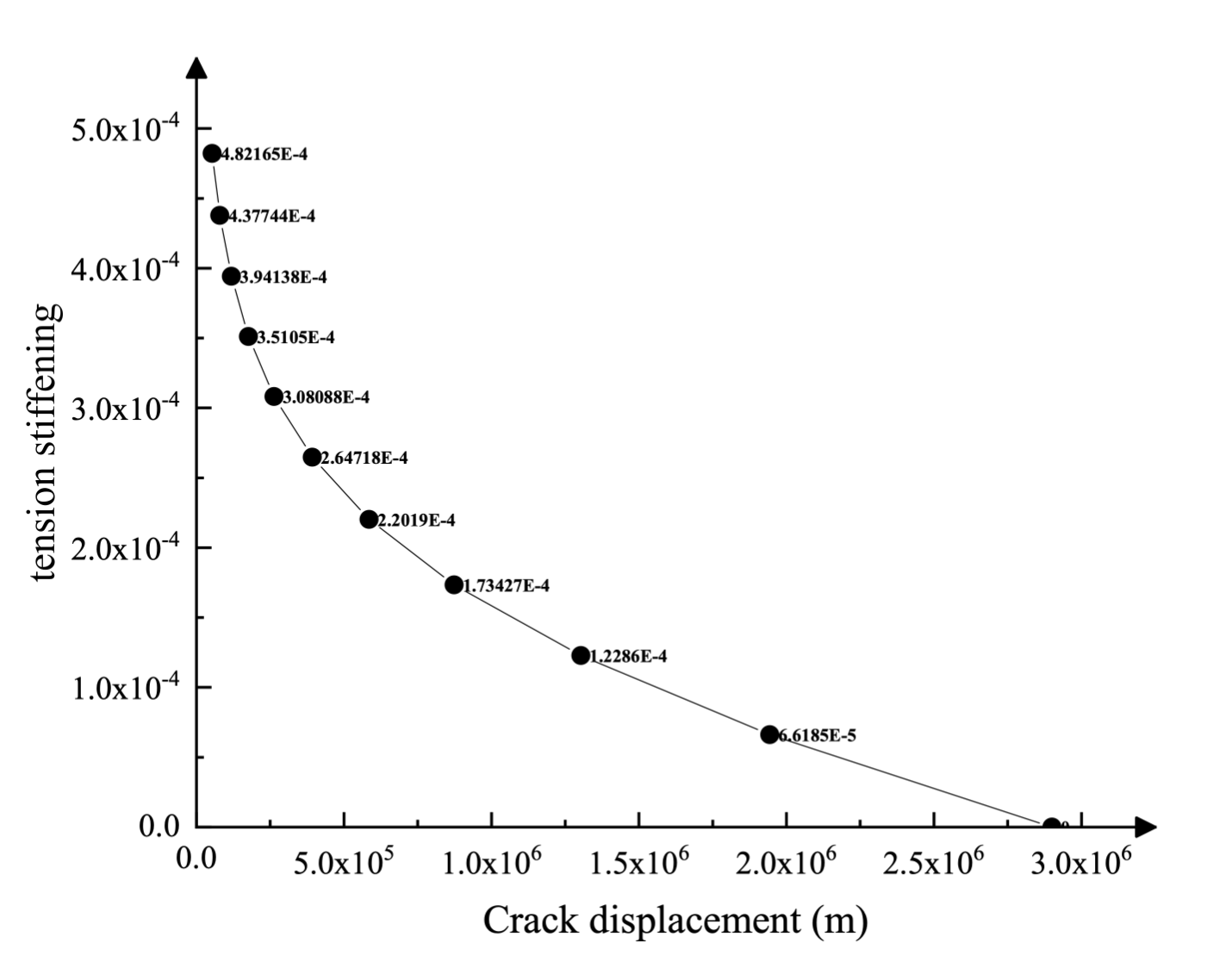
同様に、引張損傷は、亀裂後の損傷変位曲線を使用して、亀裂変位の関数として表形式で指定されます。曲線は図4.2に示されています。コンクリートの圧縮破壊(圧壊)による剛性低下被害はゼロと仮定します。
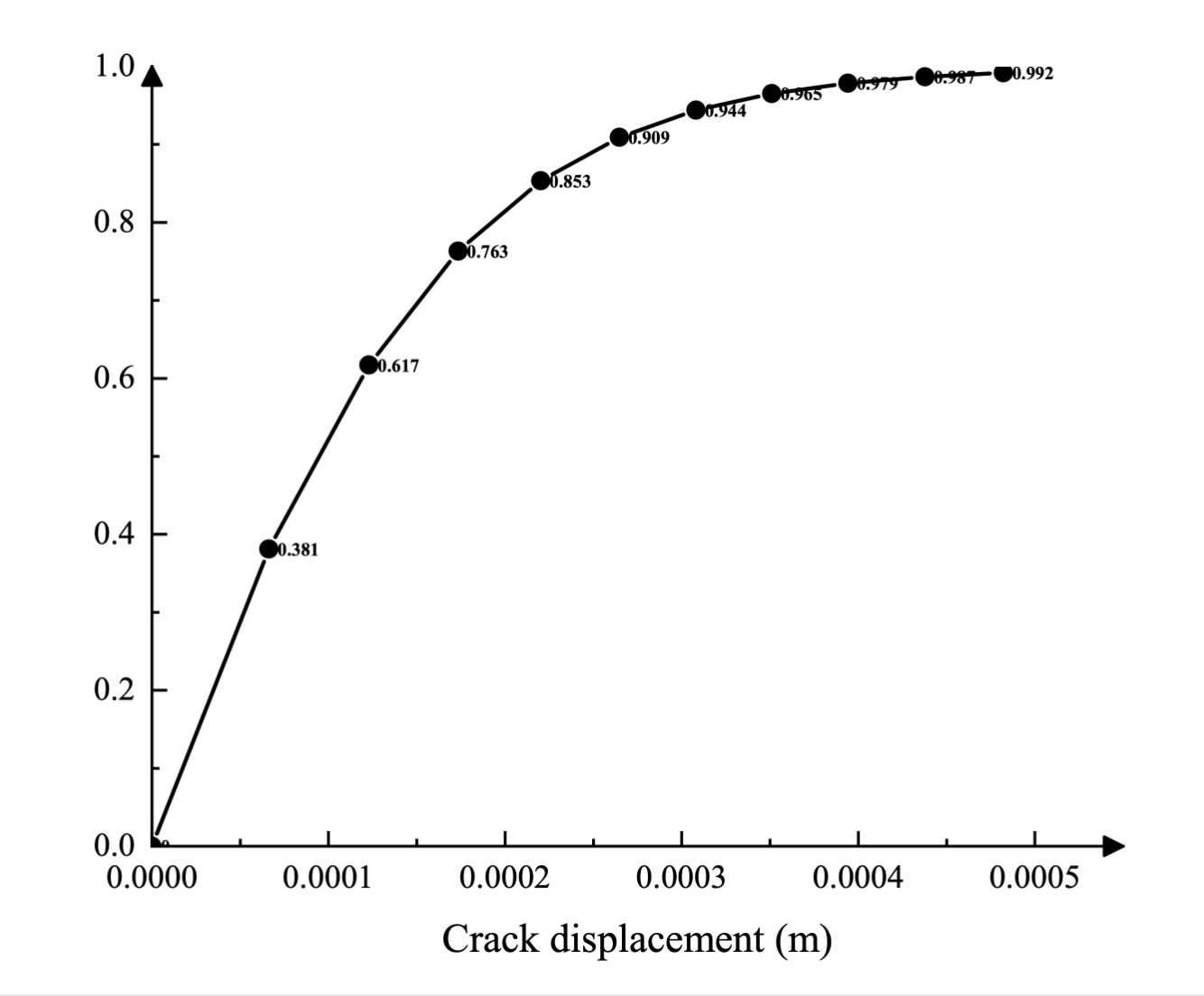
ケース1: 周波数領域解析
コンクリートダムの周波数解析は、主に以下の点で水利プロジェクトにおいて非常に重要です。
1. 耐震性能評価
高いコンクリートダムは通常、地震が発生しやすい地域に設置されるため、耐震性が安全な運用の鍵となります。周波数解析により、地震時のダムの動的応答特性を把握し、耐震性を評価することができます。たとえば、周波数解析は、地震の作用下にあるダムの固有周波数と振動モードを決定するのに役立ち、それによってダムの耐震性能を評価することができます3。
2. 動的特性解析
周波数解析により、固有周波数、振動モード、減衰比などのダムの動的特性を明らかにすることができます。これらの動的特性は、ダムの動的応答と動作を理解する上で非常に重要です。たとえば、周波数解析を使用すると、さまざまな水位や荷重条件下でのダムの固有周波数の変化を把握し、動的安定性を評価することができます。
- 次の図は、コイナの最初の4つの振動モードを示しています。
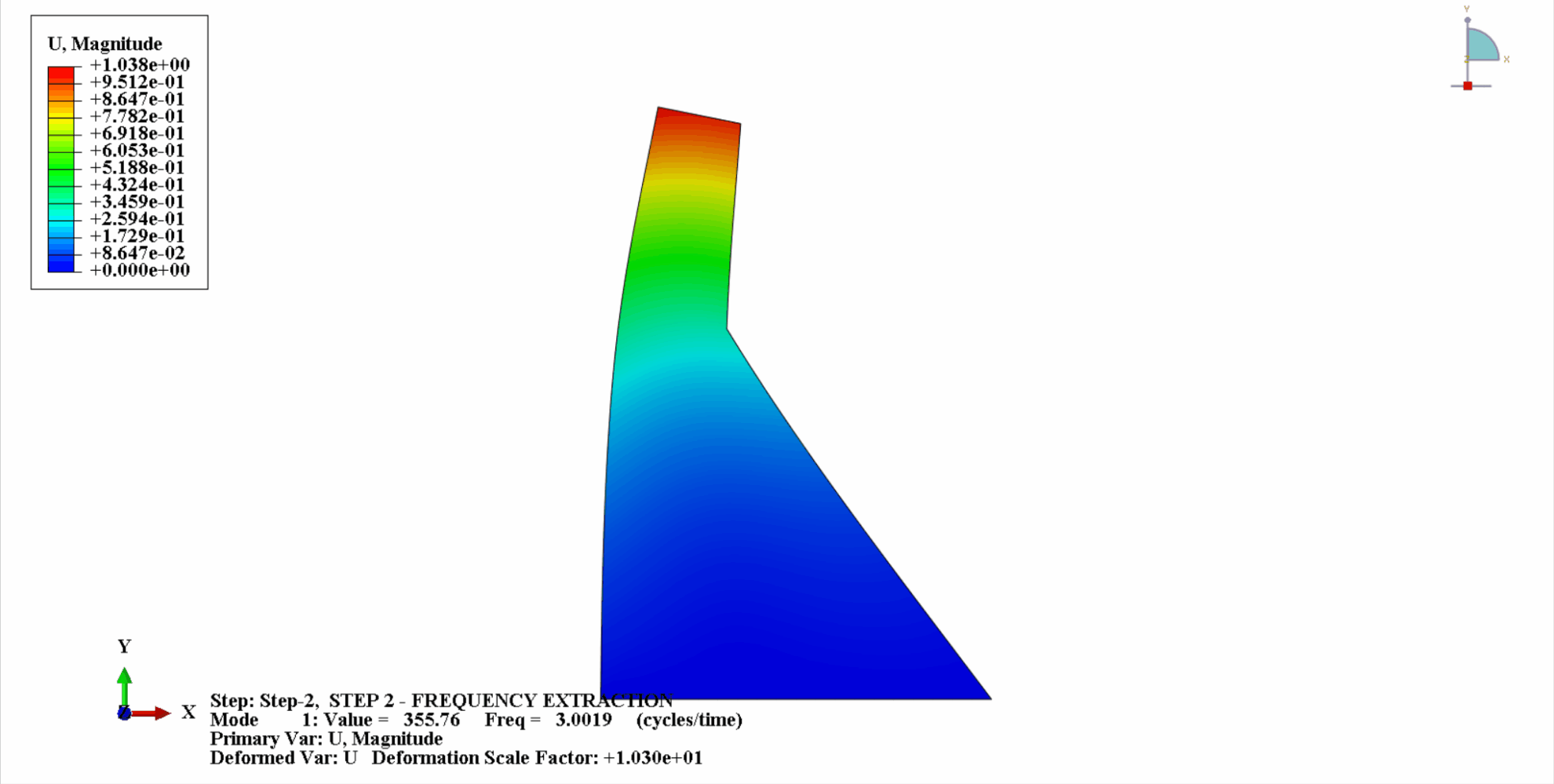
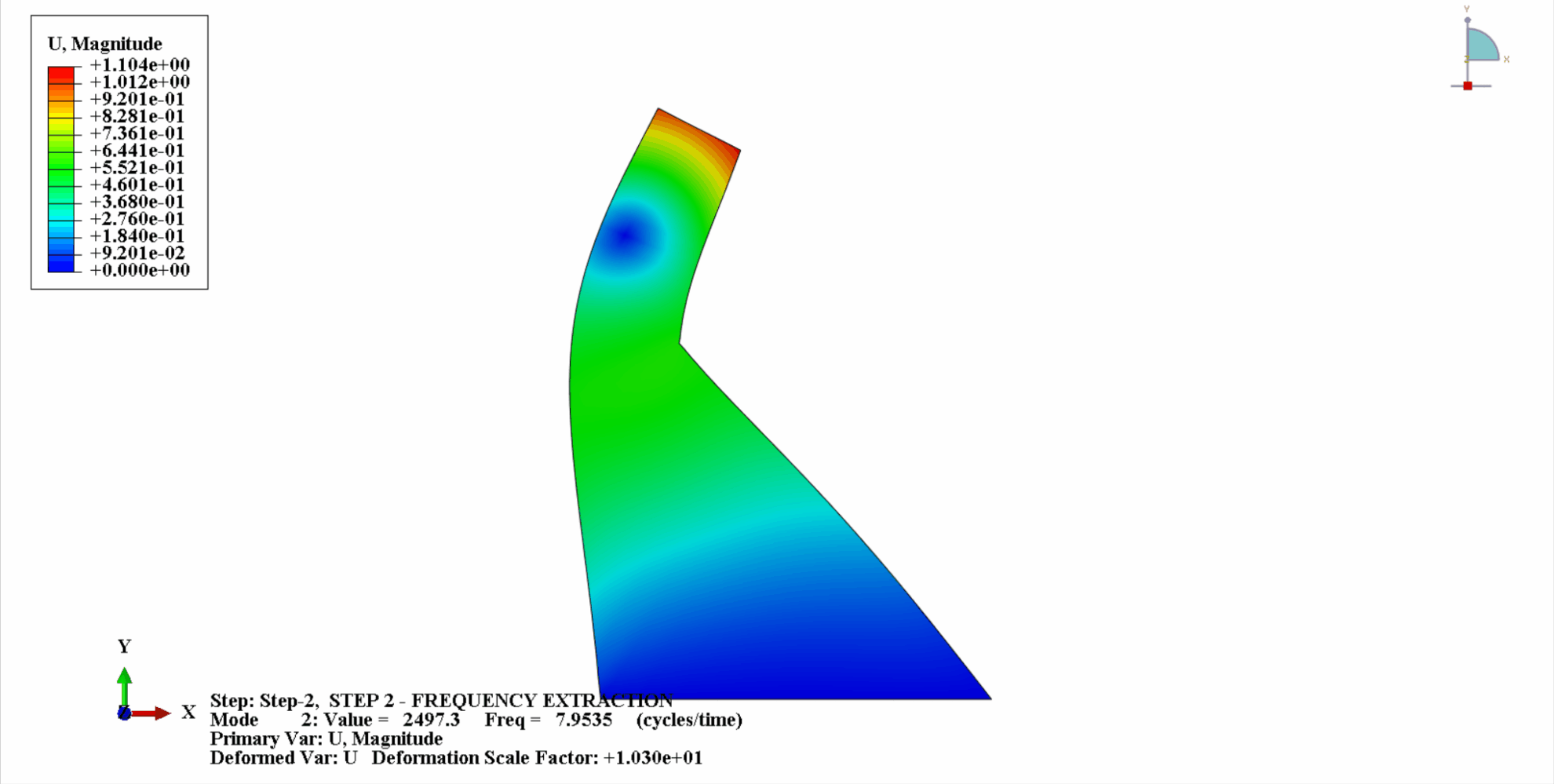
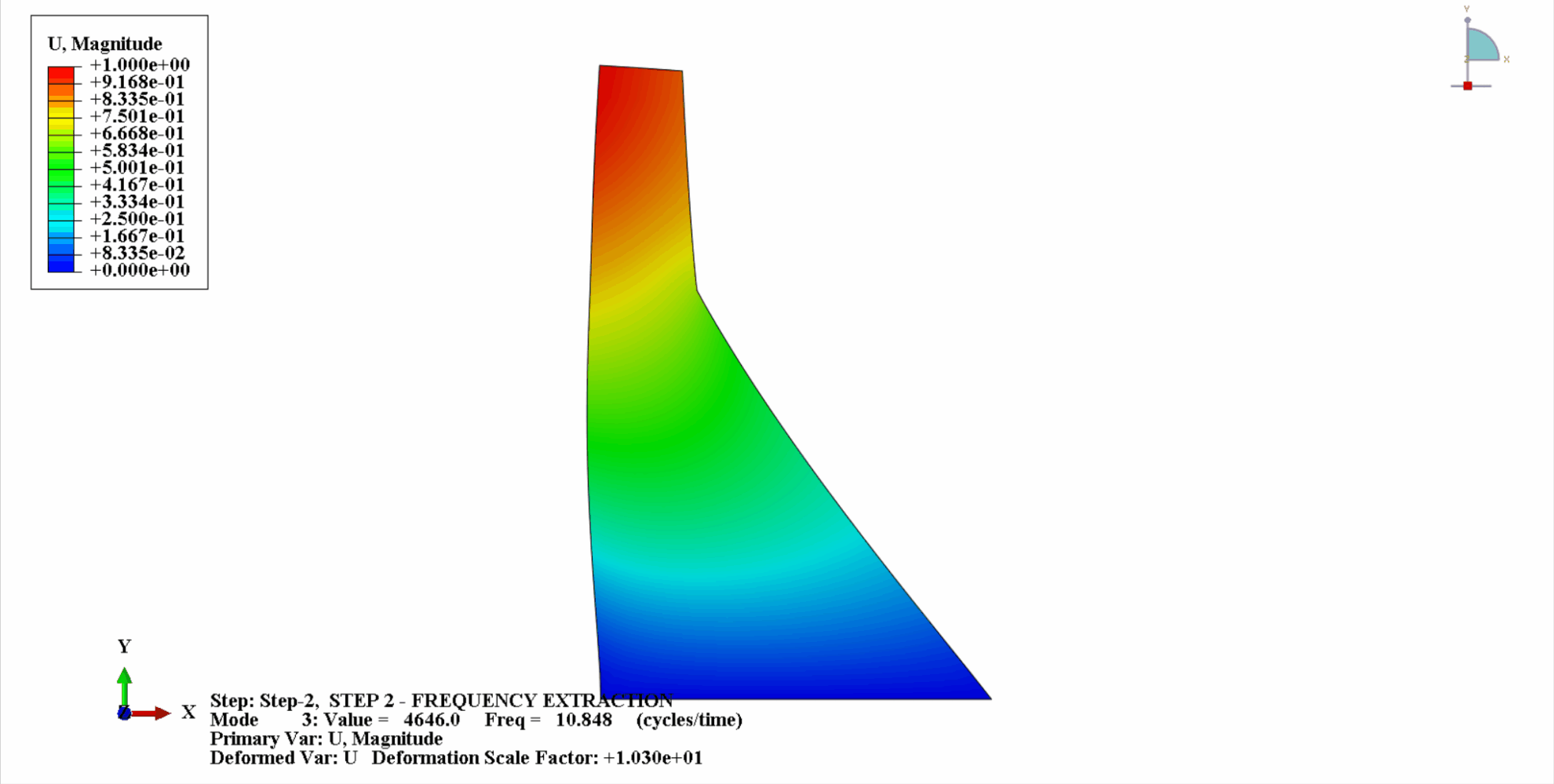
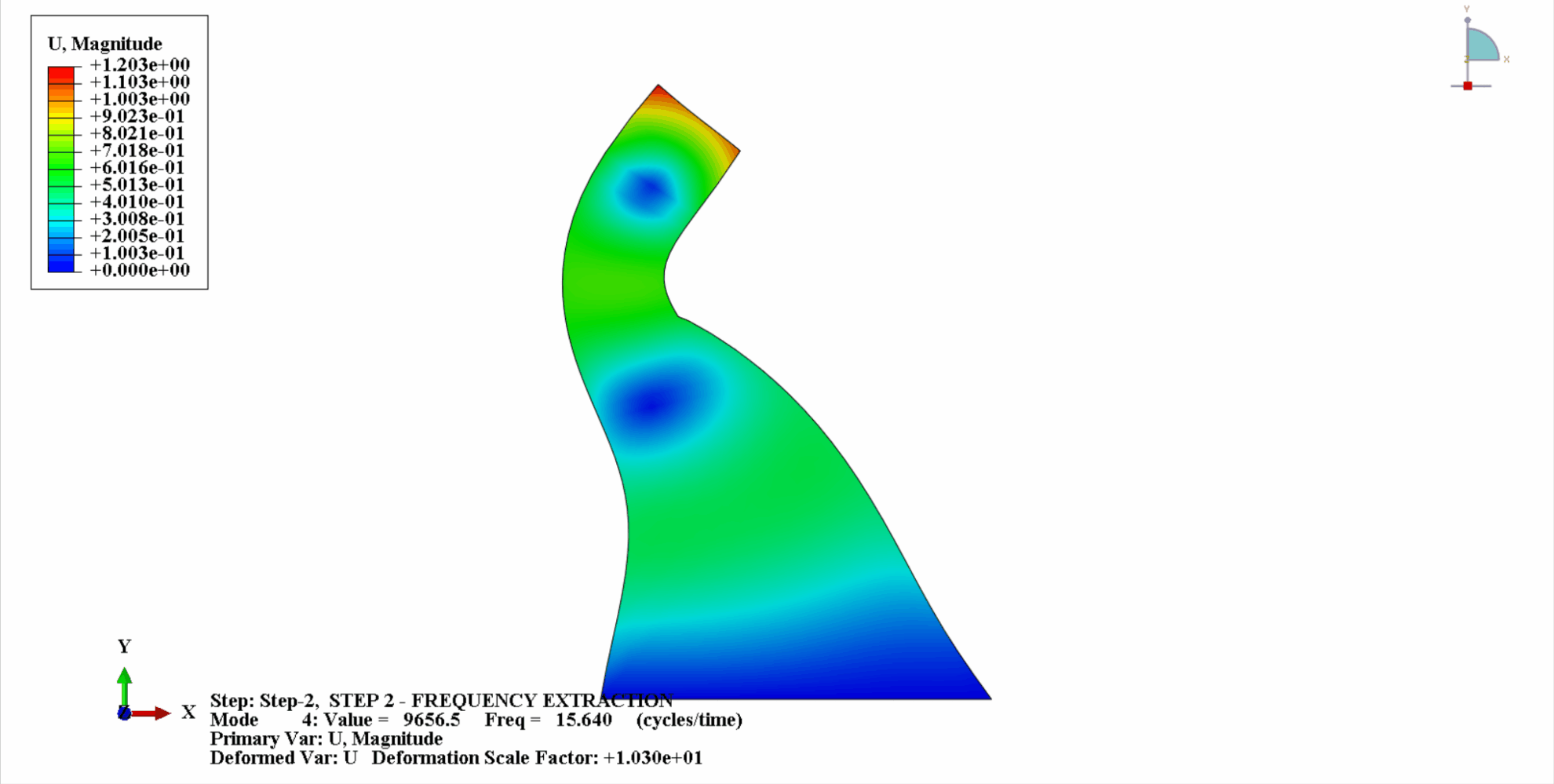
- 次の表は固有振動数の比較を示しています。この例の計算結果は Chopra の計算と一致しており、計算誤差は許容範囲内であることがわかります。
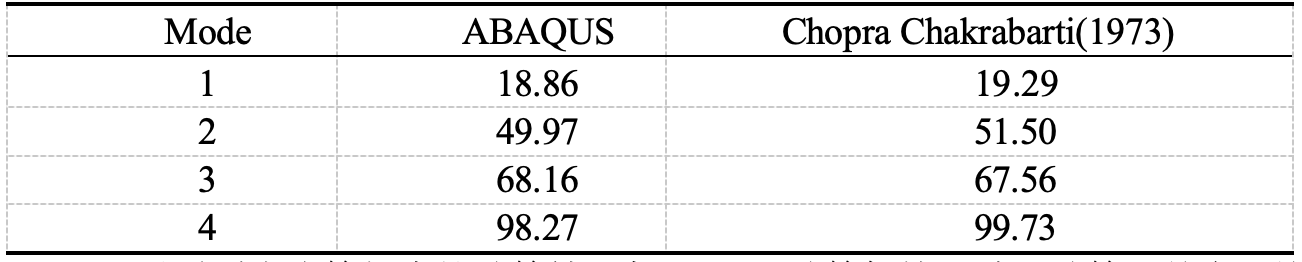
この例の計算結果は Chopra の計算と一致しており、計算誤差は許容範囲内であることがわかります。
事例3:地震応答解析 - 動水圧を考慮した
コンクリートダムの地震応答解析では、相対変位データ、相対速度、相対加速度データなど、ダム頂部とダムベル間の相対データに主な焦点が当てられます。
* 以下は、川に沿ったダムの頂上とダムベルの相対変位の時刻歴曲線です。
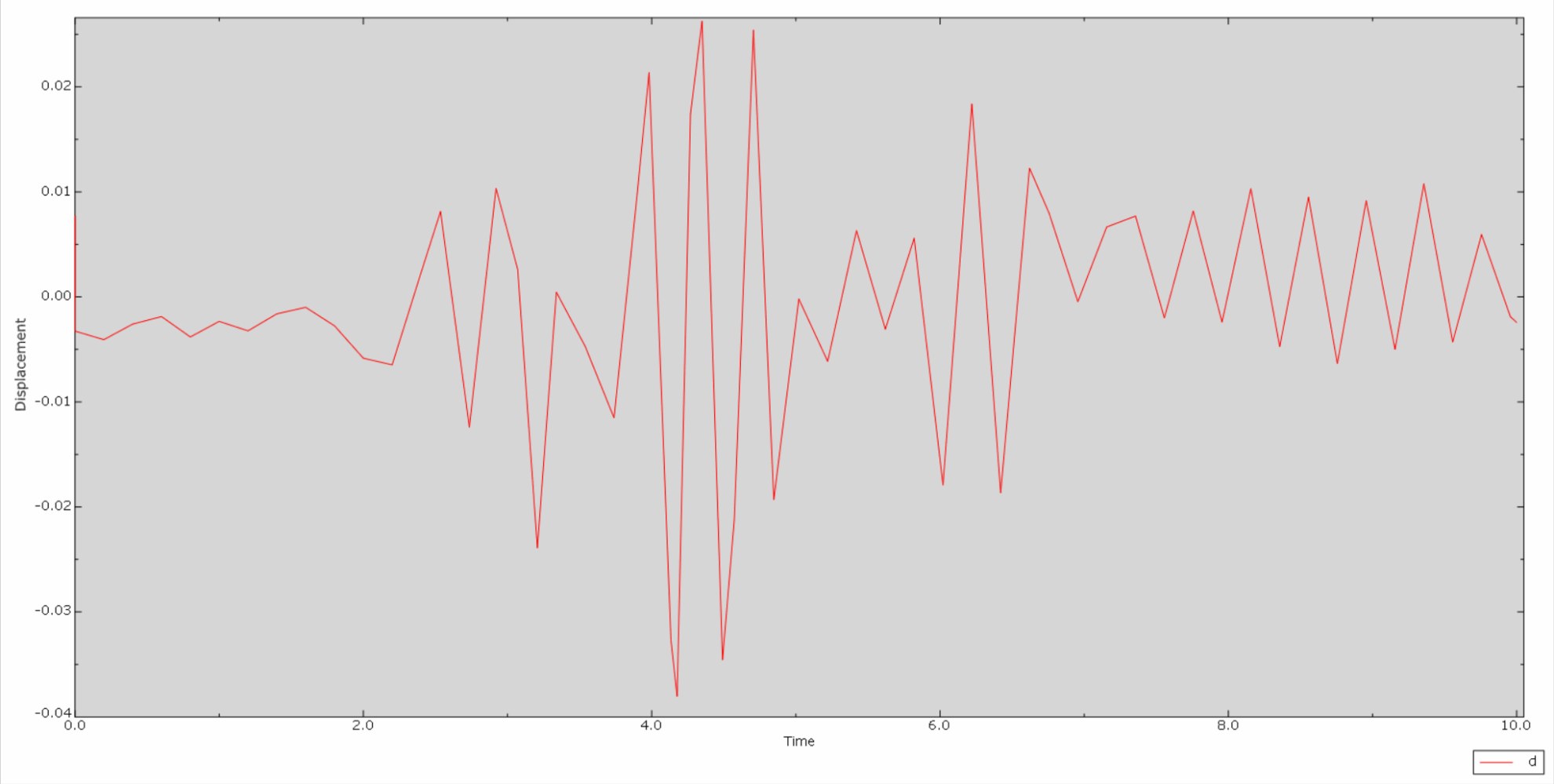
*ダムの頂部とダムベル間の相対速度の時間履歴曲線は次のとおりです。
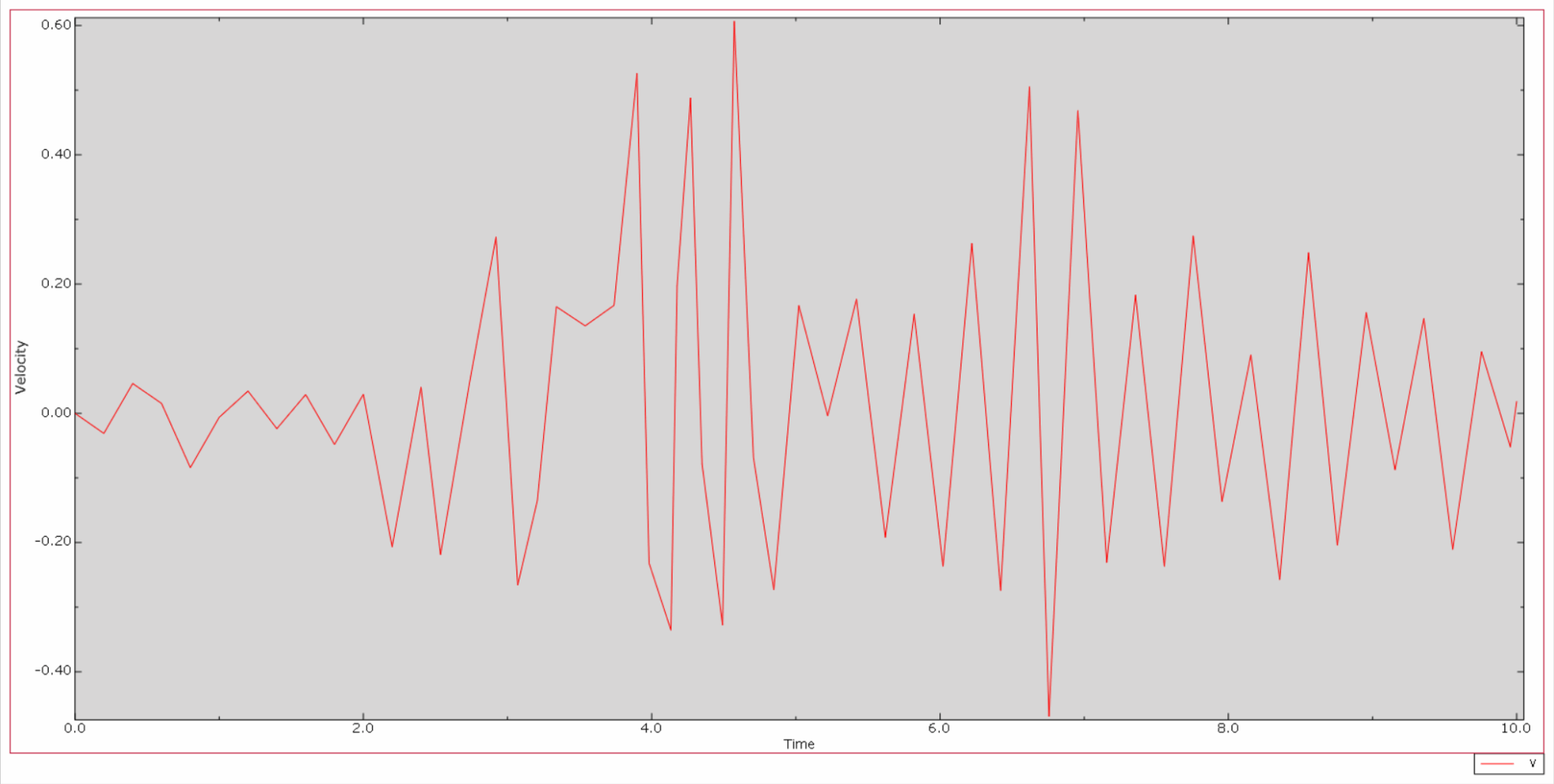
*ダム頂部とダムベルの相対加速度時刻歴曲線は次のようになります。
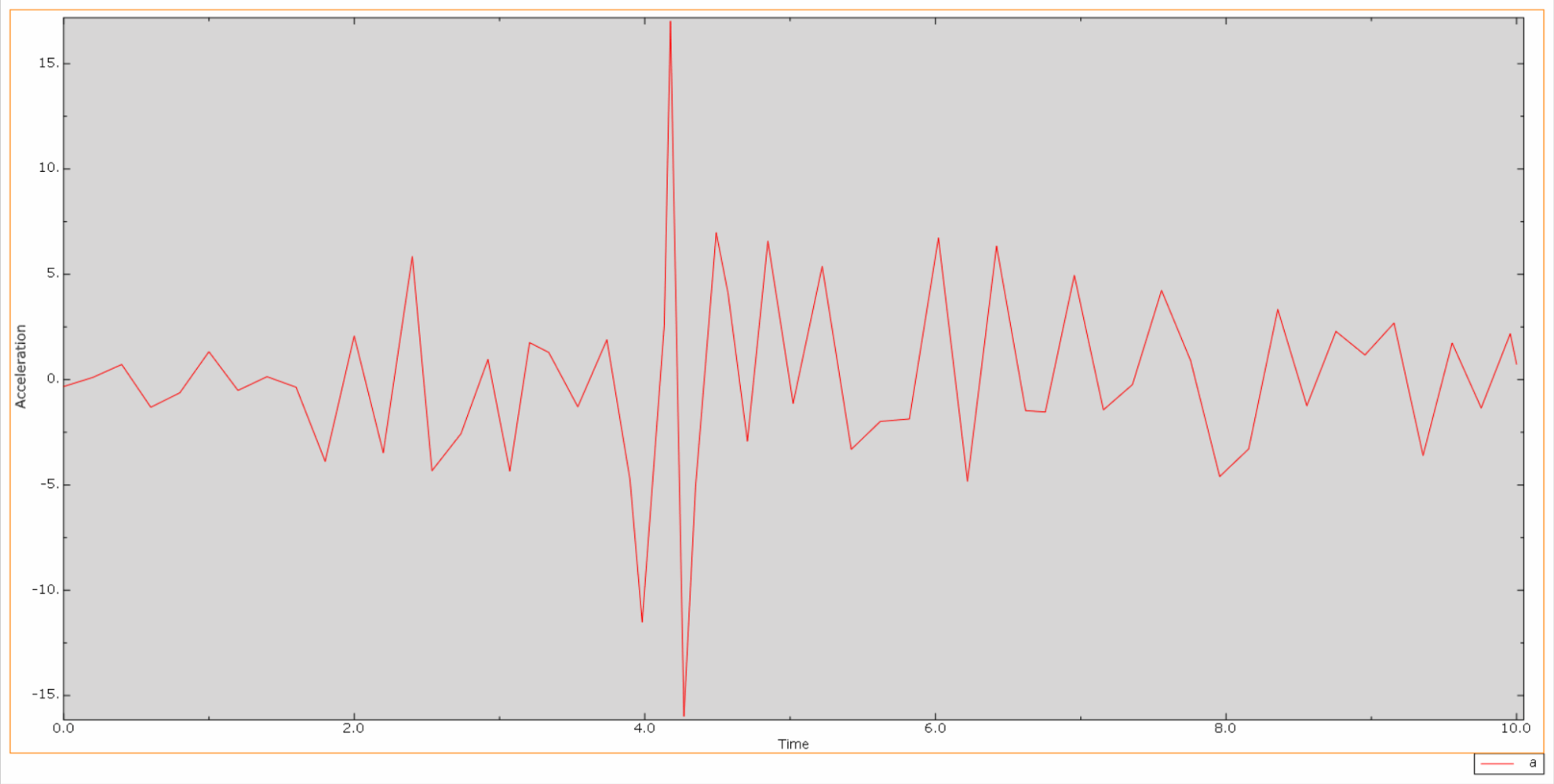
地震の作用により、コンクリートダムの材料は周期的な引張‐圧縮状態となり、コンクリートが損傷します。以下は、ダム本体の引張損傷を時間経過とともにクラウド化した図である。
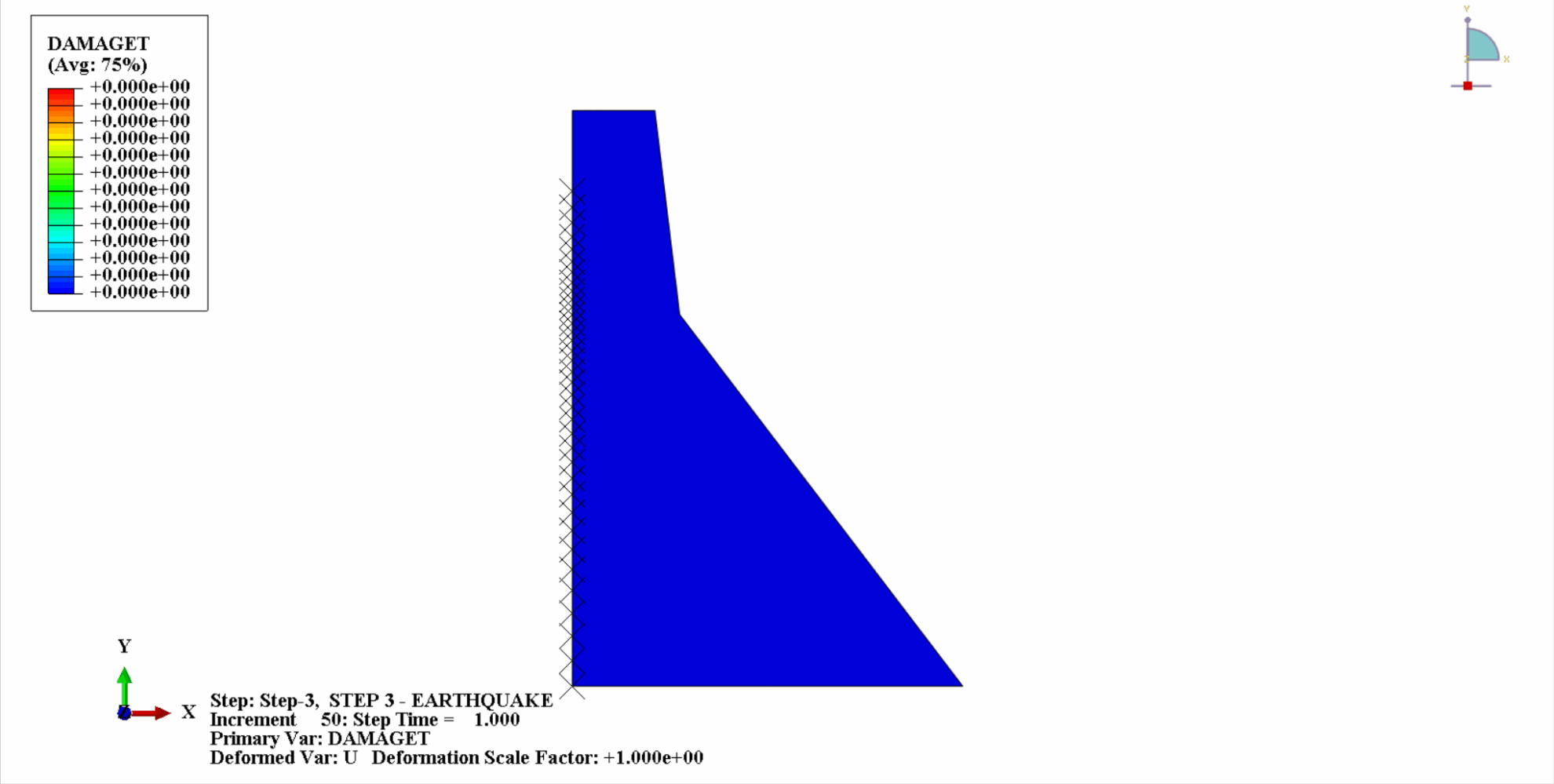
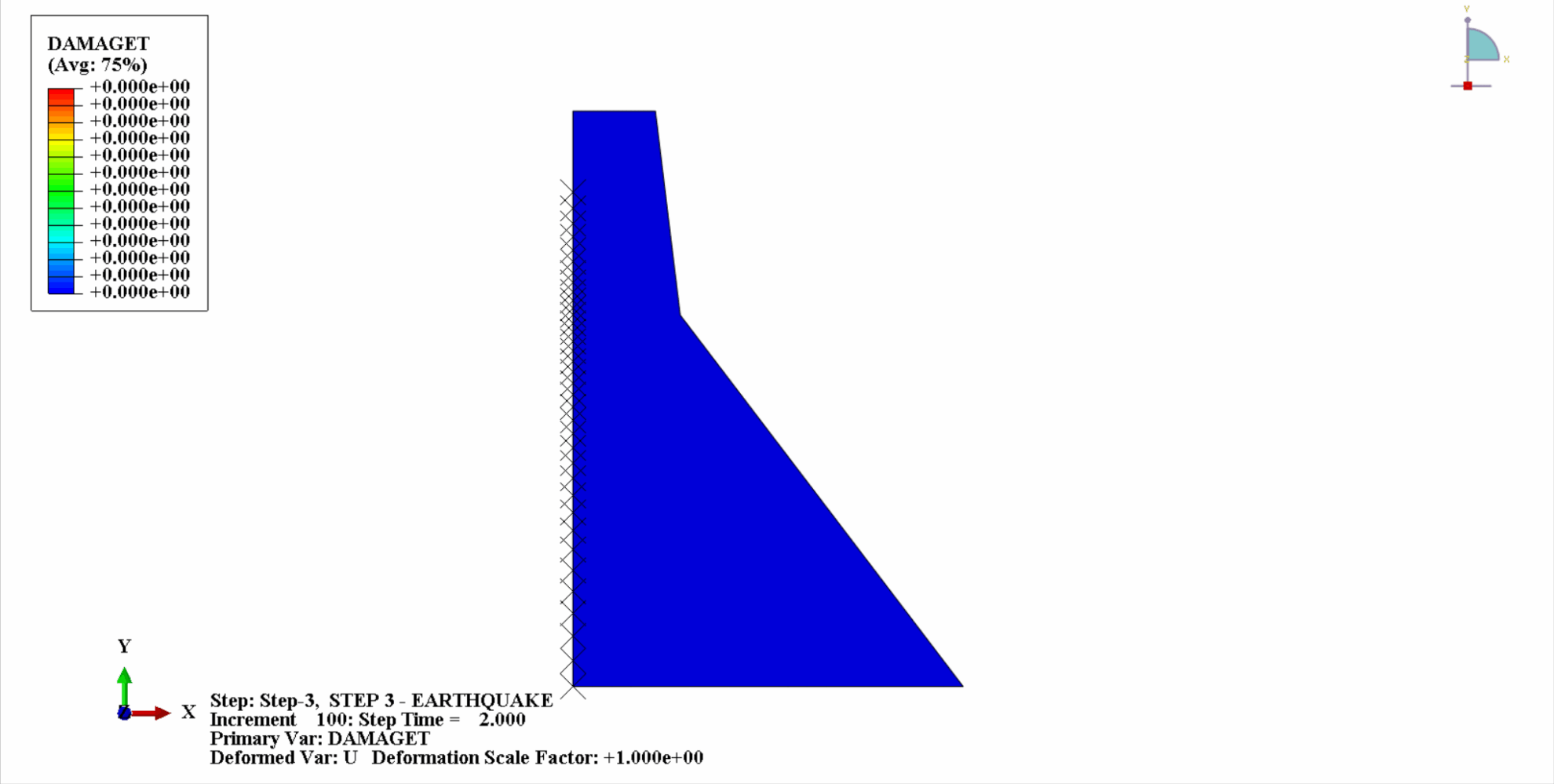
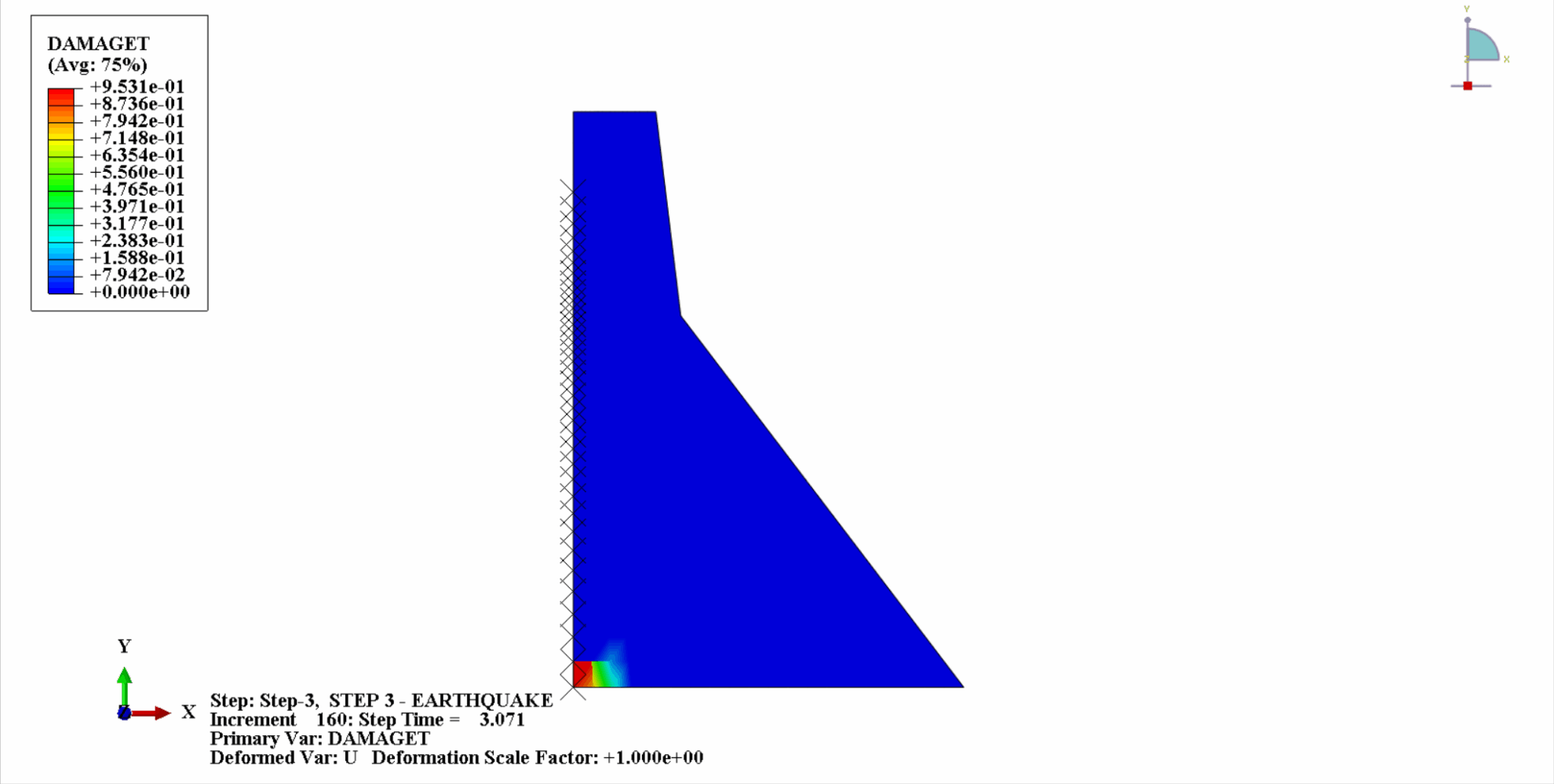
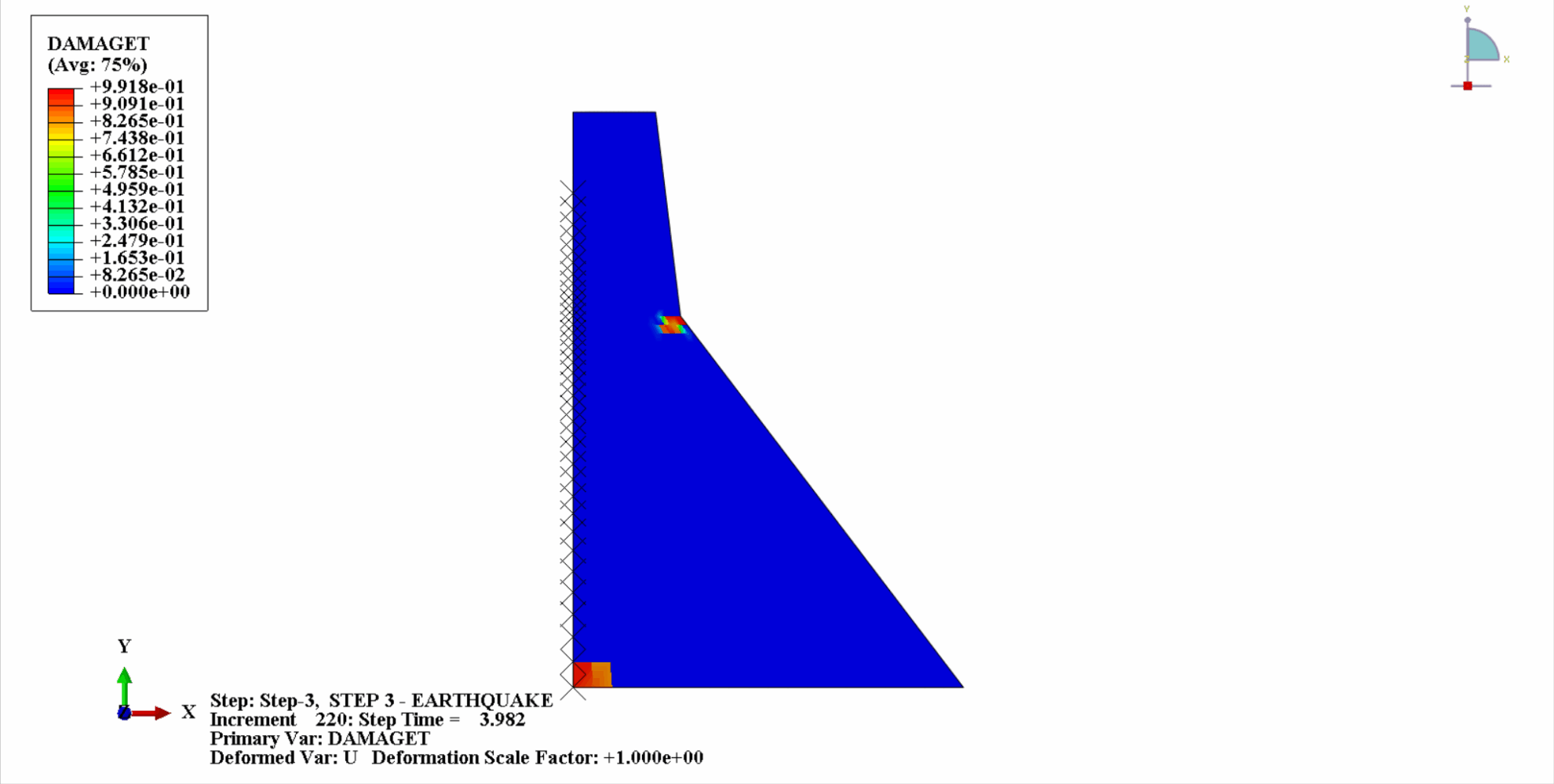
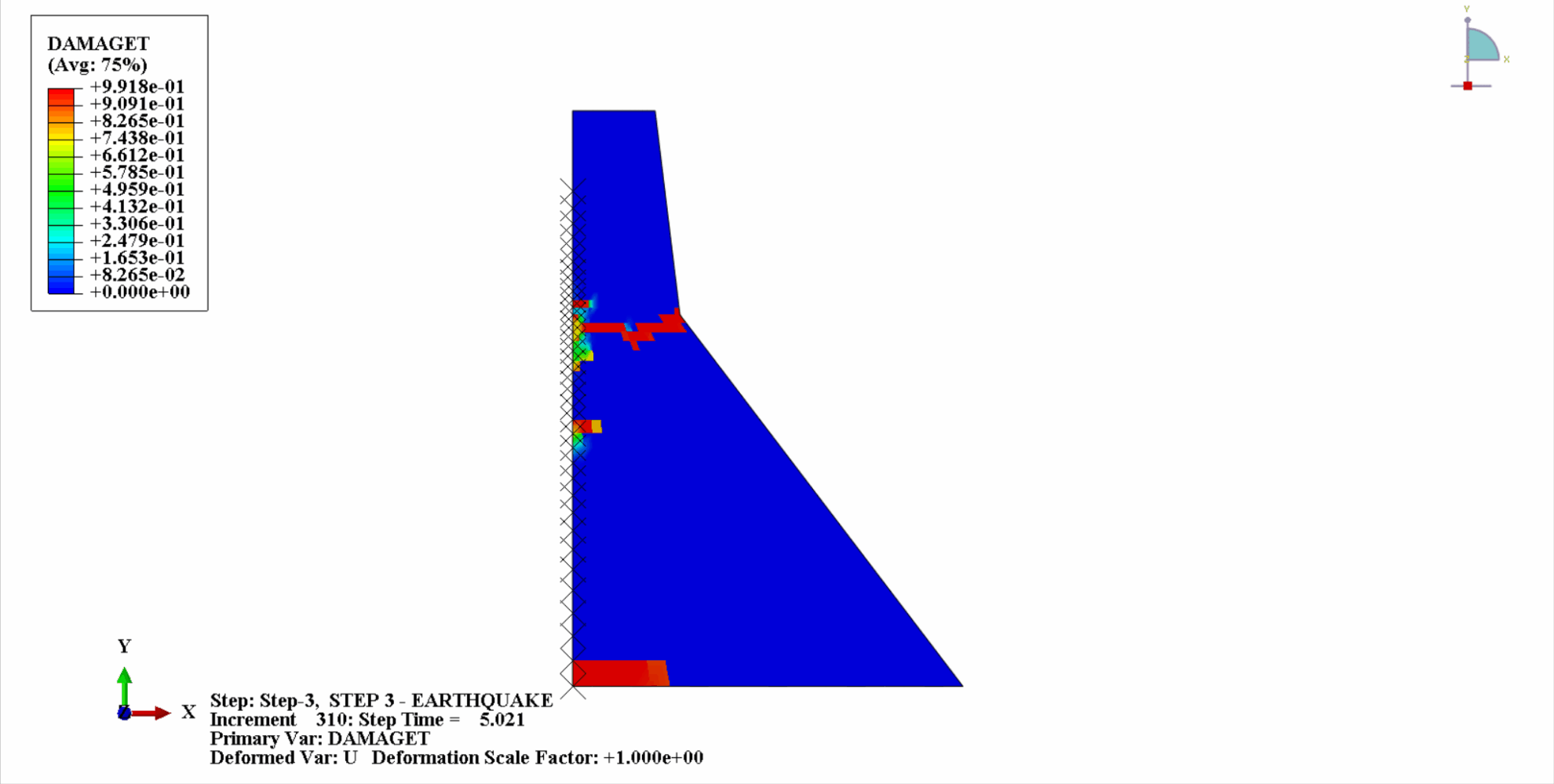

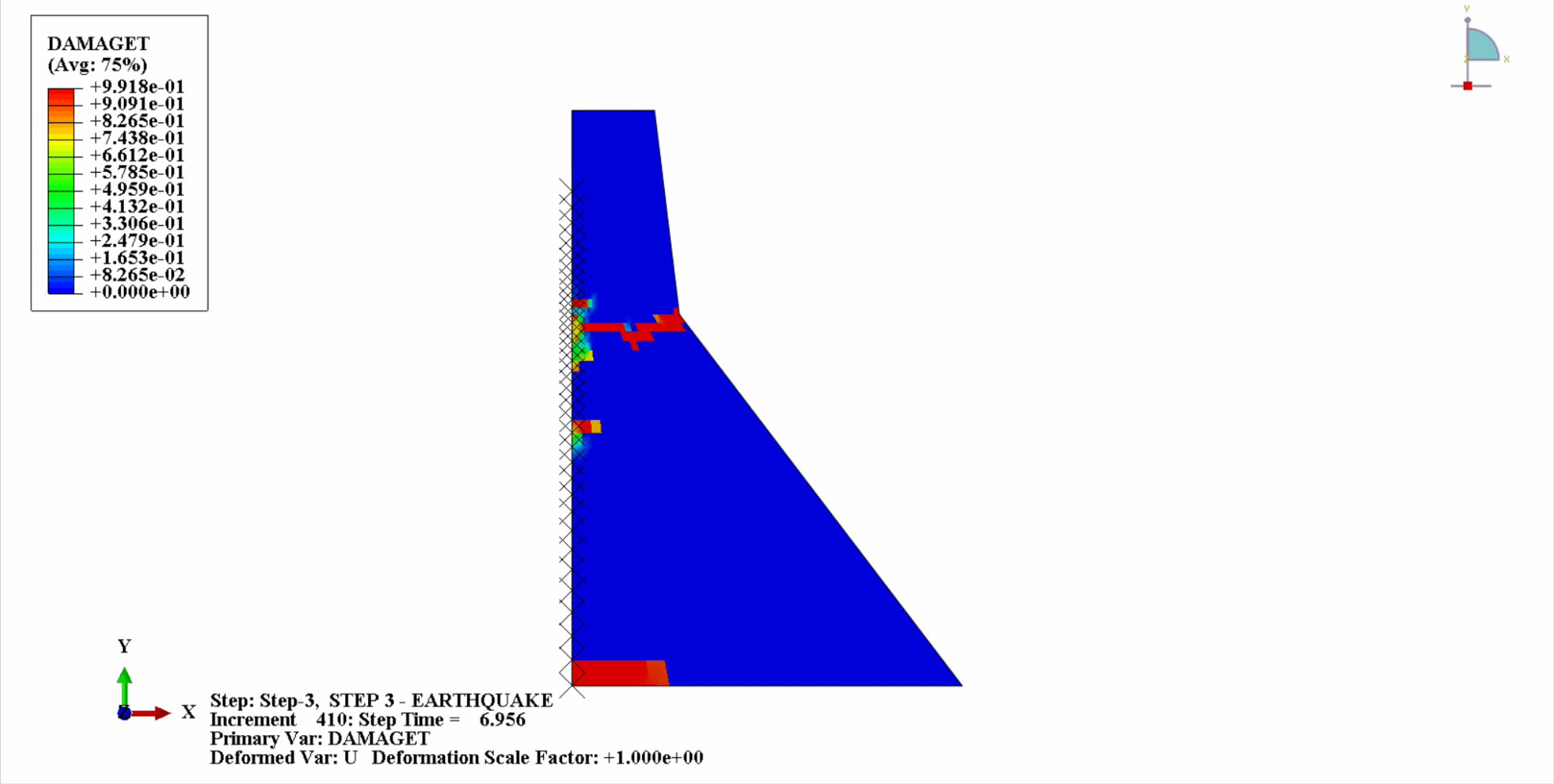
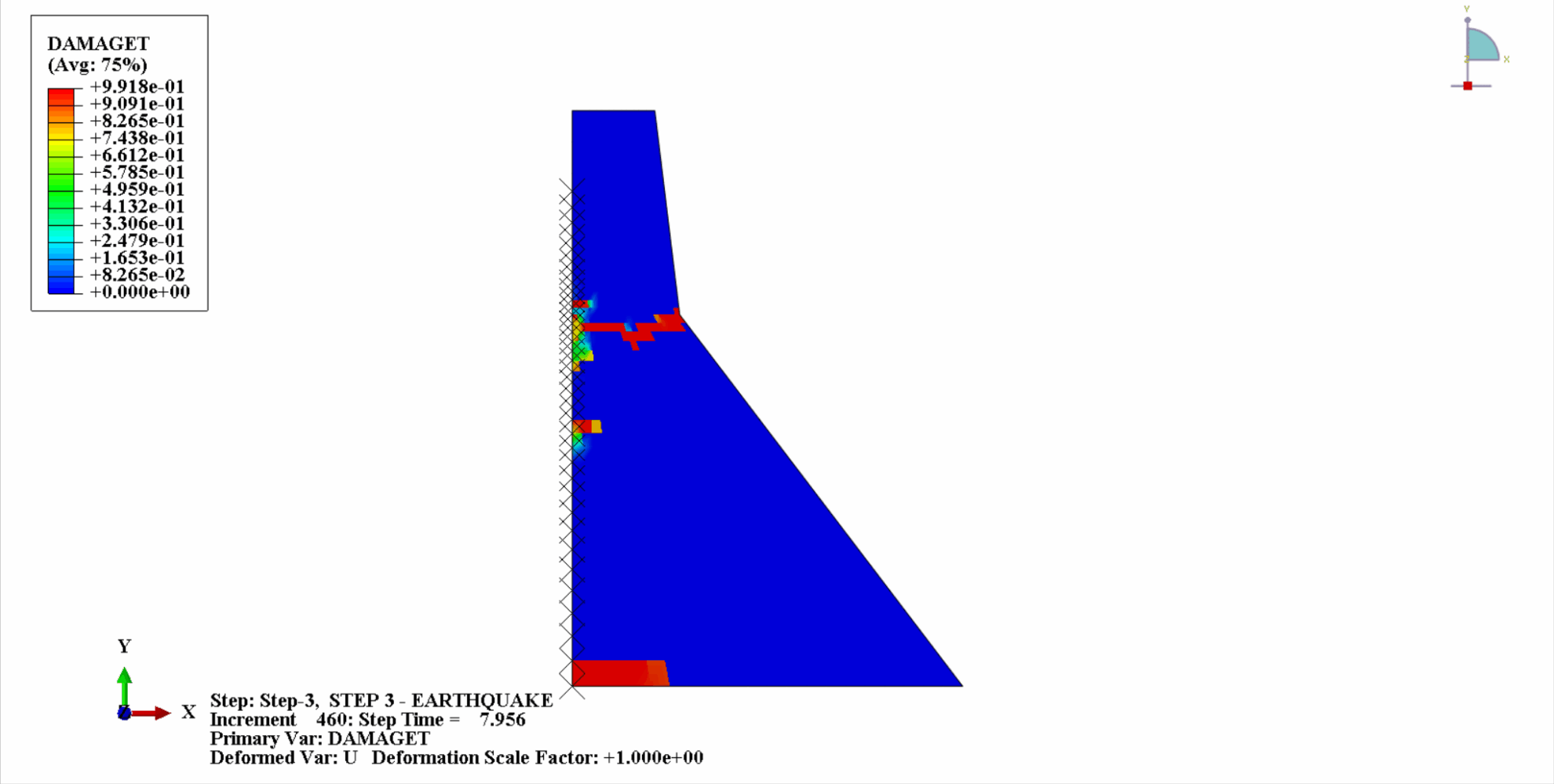
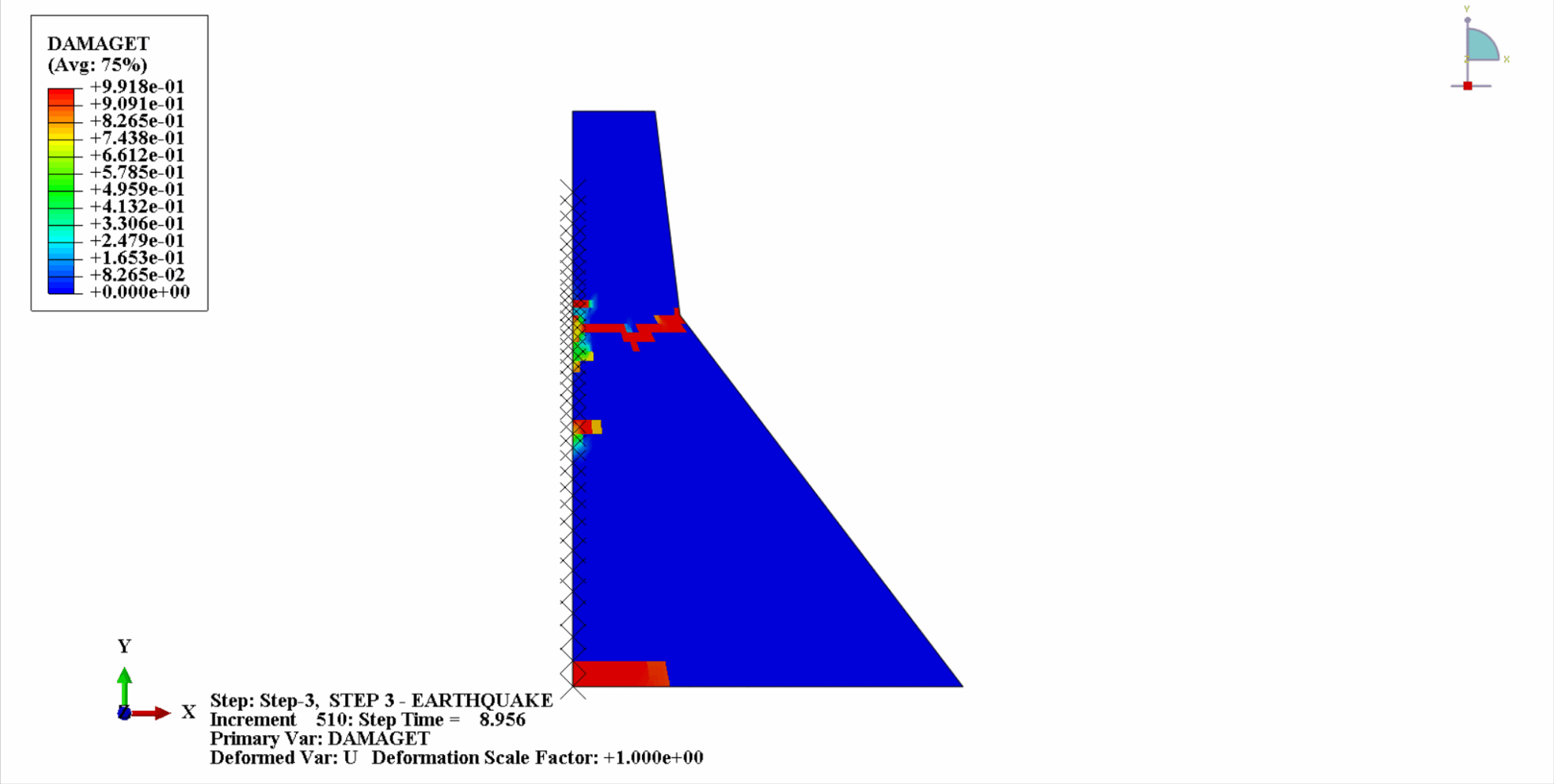
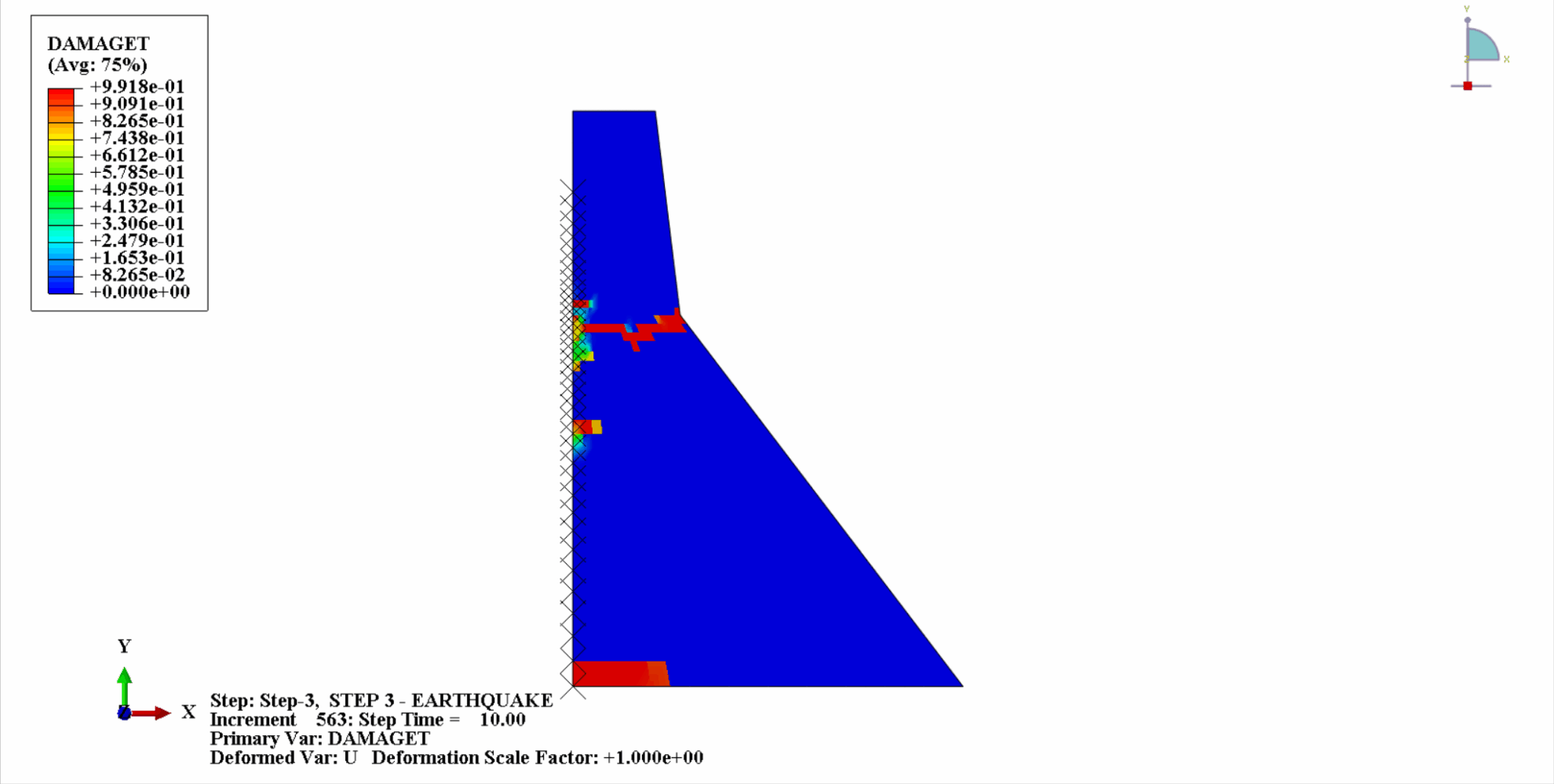
時間の経過とともに、ダムコンクリートの引張損傷が徐々に蓄積していくことがわかります。地震の最後の瞬間に被害は最大に達します。コンクリートダムの引張損傷部位は、主にダム中央部とダム本体の上流・下流褶曲法面に集中しています。