One-sentence Summary

Researchers from Renmin University and Tencent propose G-OPD, a generalized on-policy distillation framework with reward scaling and flexible reference models, enabling students to surpass teachers via reward extrapolation (ExOPD), especially in multi-expert merging and strong-to-weak settings.

Key Contributions

• We theoretically unify on-policy distillation (OPD) with dense KL-constrained reinforcement learning, showing that OPD is a special case where reward and KL terms are equally weighted and the reference model is arbitrary, enabling a generalized framework (G-OPD) with flexible reward scaling and reference model selection.
• We introduce ExOPD, a variant of G-OPD with reward scaling >1, which consistently outperforms standard OPD across teacher-student pairings and enables students to surpass domain-specific teachers when merging multiple RL-finetuned experts, validated on 4 math and 3 code generation benchmarks.
• In strong-to-weak distillation, we show that using the teacher’s pre-RL model as the reference in ExOPD improves reward accuracy and distillation performance, though it requires additional compute and access to the teacher’s base model, further boosting results over standard OPD.

Introduction

The authors leverage on-policy distillation (OPD) — where a student model learns from teacher logits on its own generated trajectories — to improve LLM post-training, especially in merging domain-specific capabilities or distilling large teachers into smaller students. Prior OPD methods treat reward and KL regularization as fixed-equal components, limiting their flexibility and potential to exceed teacher performance. The authors’ main contribution is Generalized OPD (G-OPD), which introduces a reward scaling factor and flexible reference model; they show that scaling rewards above 1 (ExOPD) lets students surpass teachers, particularly in multi-teacher fusion and strong-to-weak distillation, and further improve results by using the teacher’s pre-RL model as reference — though this adds computational cost.

Method

The authors leverage a generalized on-policy distillation (G-OPD) framework that extends traditional knowledge distillation by incorporating dense token-level rewards and flexible regularization control. Unlike off-policy distillation, which trains the student to mimic teacher-generated trajectories without feedback from its own actions, G-OPD operates on-policy: the student generates its own responses, and the training signal is derived from the divergence between its output distribution and that of the teacher, conditioned on the student’s own rollout.

The core of G-OPD lies in its reformulation of the on-policy distillation objective using a reference model $\pi_{\text{ref}}$πref​ and a reward scaling factor $\lambda$λ. Starting from the standard OPD objective, which minimizes the reverse KL divergence between the student $\pi_{\theta}$πθ​ and teacher $\pi^{*}$π∗ over student-generated trajectories, the authors re-express this as a KL-constrained reinforcement learning objective. Specifically, they show that OPD is equivalent to maximizing a reward function $r(x, y) = \log \frac{\pi^{*}(y|x)}{\pi_{\text{ref}}(y|x)}$r(x,y)=logπref​(y∣x)π∗(y∣x)​ while penalizing deviation from $\pi_{\text{ref}}$πref​ via a KL term. This equivalence allows them to introduce $\lambda$λ to modulate the relative weight of the reward versus regularization, yielding the generalized objective:

This formulation enables two key operational regimes. When $0 < \lambda < 1$0<λ<1, the student’s log-probability distribution is encouraged to interpolate between the teacher and reference models — a setting the authors term “reward interpolation.” When $\lambda > 1$λ>1, the student is pushed beyond the teacher’s distribution by extrapolating the reward signal, which they call “reward extrapolation.” This flexibility allows practitioners to tune the student’s behavior along a spectrum from conservative imitation to aggressive optimization.

In the strong-to-weak distillation setting — where a large teacher is distilled into a smaller student — the authors propose a “reward correction” mechanism. Instead of using the student’s base model as the reference, they advocate for using the teacher’s pre-RL base model $\pi_{\text{base}}^{\text{teacher}}$πbaseteacher​, which yields a cleaner implicit reward signal aligned with the teacher’s RL training trajectory. This correction adjusts the reward from $\log \frac{\pi^{*}}{\pi_{\text{base}}^{\text{student}}}$logπbasestudent​π∗​ to $\log \frac{\pi^{*}}{\pi_{\text{base}}^{\text{teacher}}}$logπbaseteacher​π∗​, effectively compensating for architectural and capacity mismatches between teacher and student base models.

The training dynamics are governed by a policy gradient estimator derived from the G-OPD objective. The approximated gradient, computed under a zero discount factor for computational efficiency, takes the form:

where the token-level advantage is defined as:

This advantage function encapsulates both the student-teacher mismatch and the reference-induced reward shift, enabling dense, per-token credit assignment that accelerates convergence and improves generalization.

Experiment

• Single-teacher distillation shows that standard OPD fully recovers teacher behavior, while reward interpolation (0 < λ < 1) enables controlled trade-offs between performance and response length; reward extrapolation (λ = 1.25) consistently surpasses the teacher, though λ = 1.5 risks instability due to reward hacking.
• In multi-teacher distillation, ExOPD with λ = 1.25 outperforms both OPD and SFT, producing a unified student that exceeds all domain teachers—unlike weight extrapolation (ExPO), which lacks consistent gains and controllability.
• In strong-to-weak distillation, ExOPD significantly outperforms standard OPD and SFT, demonstrating that reward extrapolation can overcome knowledge gaps between large and small models.
• Reward correction—using the teacher’s pre-RL variant as reference—further boosts ExOPD performance, though it incurs higher computational cost and requires access to additional model variants.
• Across settings, ExOPD consistently increases response length and entropy, indicating greater output diversity, while maintaining or exceeding teacher-level accuracy.

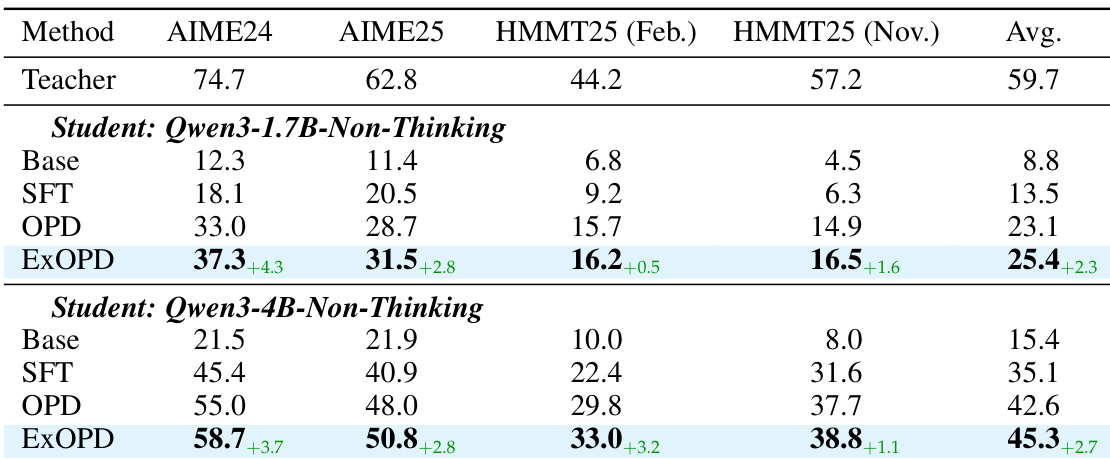
The authors use ExOPD to distill knowledge from stronger teacher models into smaller students in a strong-to-weak setting, achieving consistent improvements over standard OPD and SFT across multiple math reasoning benchmarks. Results show that ExOPD not only outperforms baseline methods but also scales effectively with student model size, delivering larger gains for smaller students. The method demonstrates robustness to model capacity gaps, suggesting reward extrapolation can push beyond standard distillation limits even when teachers and students differ significantly in scale.

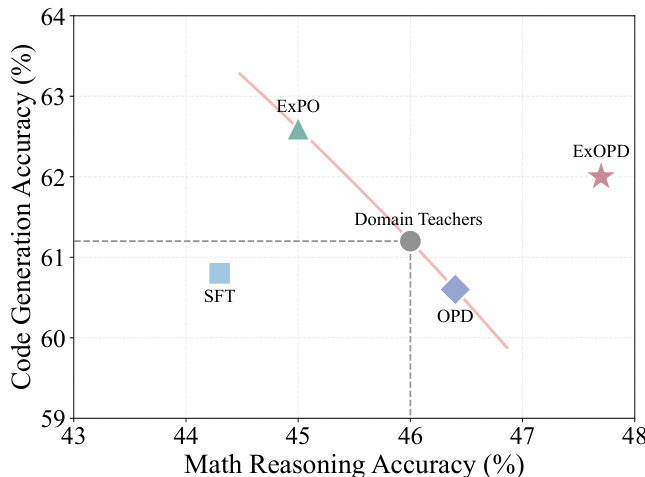
The authors use ExOPD with a reward scaling factor of 1.25 to distill knowledge from domain-specific teachers into a base model, achieving consistent performance gains over standard OPD and the original teachers across both math reasoning and code generation tasks. In multi-teacher settings, ExOPD is the only method that produces a unified student surpassing all individual domain teachers, while SFT and ExPO show limited or inconsistent improvements. Results also confirm that ExOPD’s gains are not due to insufficient teacher training, as continued RL on teachers yields smaller improvements than ExOPD with fewer steps.

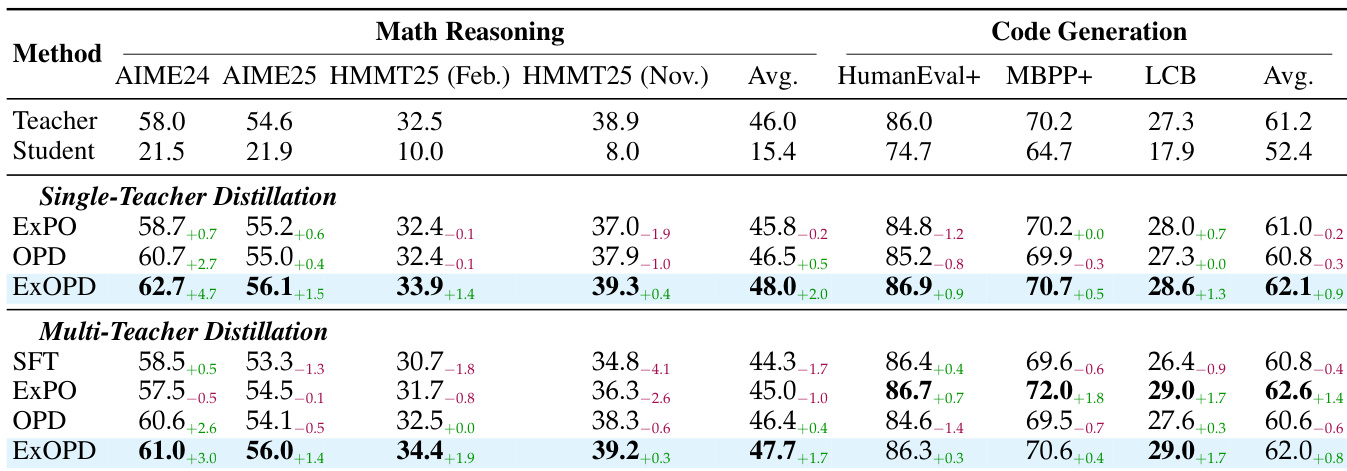
The authors use ExOPD with a reward scaling factor of 1.25 to distill knowledge from domain-specific teachers into a base model, achieving performance that exceeds both the original teacher and standard OPD. Results show that even with fewer training steps, ExOPD consistently outperforms the teacher model across multiple math reasoning benchmarks, indicating its ability to push beyond the teacher’s capabilities. This improvement is not due to extended teacher training, as additional RL steps on the teacher yield smaller gains compared to ExOPD.