One-sentence Summary

Researchers from institutions including $^{*12}$∗12 and $^{*1}$∗1 propose a difficulty-aware advantage scaling coefficient for RLVR, inspired by Focal loss, to mitigate bias toward common trajectories. Integrated into GRPO, DAPO, and CISPO, it boosts Qwen2.5-7B’s pass@256 without added cost, improving robustness across domains.

Key Contributions

• We identify and quantify a critical sampling bias in group-relative RLVR: intermediate group sizes—common due to compute limits—maximize the probability of missing rare-correct trajectories during updates, leading to distribution sharpening despite growing total correct mass.
• We derive a closed-form tail-miss probability showing non-monotonic behavior with group size and reveal that unsampled-correct mass can shrink even as overall correctness improves, explaining conflicting prior findings on optimal rollout counts.
• We propose F-GRPO, a difficulty-aware advantage scaling inspired by Focal loss, which down-weights high-success prompts to preserve diversity; it improves pass@256 across GRPO, DAPO, and CISPO on Qwen2.5-7B without increasing group size or compute cost.

Introduction

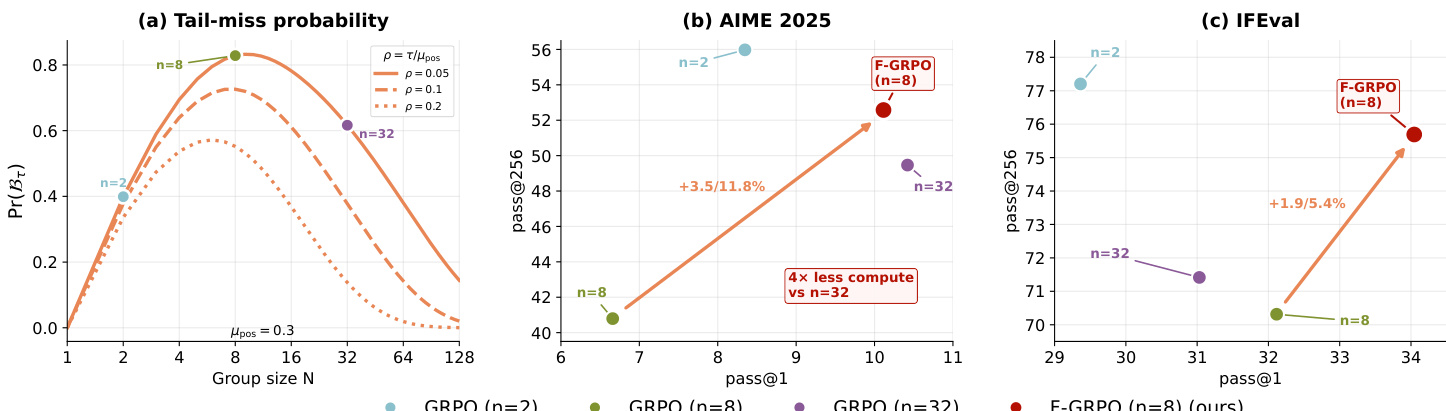
The authors leverage reinforcement learning with verifiable rewards (RLVR) to fine-tune large language models on reasoning tasks, using automatically checkable rewards to avoid costly human feedback. While RLVR improves top-1 accuracy, it often sharpens the output distribution, reducing solution diversity and hurting performance at higher sampling budgets — a trade-off that limits its effectiveness for complex or open-ended problems. Prior work offers conflicting guidance on group size in group-relative policy optimization (GRPO), with no clear consensus on how to balance exploration and efficiency. The authors’ main contribution is F-GRPO, a lightweight, difficulty-aware scaling of advantages that mitigates sharpening without increasing rollout count. It targets intermediate group sizes — where sharpening is worst — and recovers high-k performance (e.g., pass@256) while preserving pass@1, using 4x fewer rollouts than larger groups.

Dataset

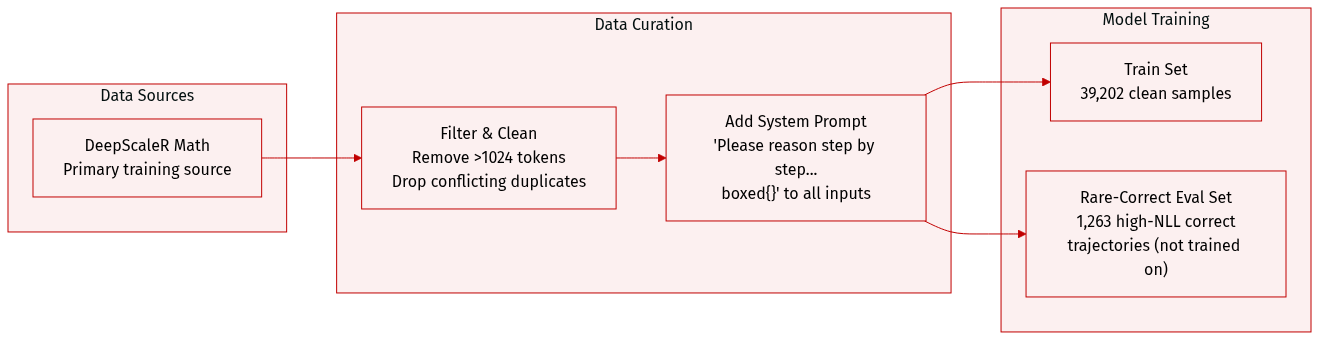
• The authors use the DeepScaleR math dataset (Luo et al., 2025) as the primary training source, filtering out samples longer than 1024 tokens and removing duplicates with conflicting answers, resulting in 39,202 clean training samples.
• They prepend a fixed system prompt — “Please reason step by step, and put your final answer within \boxed{}.” — to every training input to standardize reasoning format.
• For evaluating rare-correct behavior, they sample 256 prompts from the training set and generate 800 rollouts per prompt using the base model, keeping only correct trajectories.
• From these, they compute length-normalized NLL under the base model and select the top 1% highest-NLL correct trajectories as the “rare-correct” subset — totaling 1,263 trajectories — to measure how well trained models assign probability to initially unlikely correct solutions.
• This rare-correct subset is not used for training but for evaluation: higher NLL under trained models indicates the model has become less likely to generate these low-probability correct solutions.

Method

The authors leverage a difficulty-aware advantage scaling mechanism to mitigate the concentration bias inherent in group-relative reinforcement learning with verifiable rewards (RLVR). This bias arises when finite group sampling causes policy updates to disproportionately reinforce already likely correct trajectories while neglecting rare-correct modes — even as total correct mass grows. The proposed method, F-GRPO (and its variants F-DAPO and F-CISPO), introduces a lightweight, per-prompt scaling coefficient inspired by Focal loss that down-weights updates on high-success prompts, thereby preserving diversity in the solution space without increasing computational cost or group size.

At the core of the method is the observation that group-relative advantages — used in algorithms like GRPO, DAPO, and CISPO — induce a drift toward sampled-correct trajectories when the batch reward baseline $S_R > 0$SR​>0. This occurs because unsampled actions, including rare-correct ones, receive zero reward but are still penalized by the baseline subtraction in the advantage computation. The authors formalize this using a categorical policy framework, where the one-step logit update for unsampled actions $i \in U$i∈U is given by:

$$\Delta z_i = -\frac{\eta}{N} S_R p_i$$Δzi​=−Nη​SR​pi​

This update drives unsampled-correct mass downward when $S_R > 0$SR​>0, a condition that correlates strongly with high empirical success rates. To operationalize this insight at the trajectory level, they define the empirical success rate for prompt $x$x as:

$$\widehat{\mu}_{\mathrm{pos}}(x) = \frac{\bar{R}(x) - R_w}{R_c - R_w} = \frac{X}{N}$$μ​pos​(x)=Rc​−Rw​Rˉ(x)−Rw​​=NX​

where $X$X is the number of correct rollouts in the group. This statistic serves as a proxy for the magnitude of the $S_R$SR​-driven drift: higher $\widehat{\mu}_{\mathrm{pos}}(x)$μ​pos​(x) indicates stronger concentration pressure on sampled-correct trajectories.

To counteract this, the authors introduce a difficulty weight:

$$g(x) = \left(1 - \widehat{\mu}_{\mathrm{pos}}(x)\right)^\gamma, \quad \gamma \geq 0$$g(x)=(1−μ​pos​(x))γ,γ≥0

This weight scales the group-relative advantage uniformly across all rollouts from the same prompt. When $\gamma = 0$γ=0, $g(x) = 1$g(x)=1 and the method reduces to standard GRPO. For $\gamma > 0$γ>0, prompts with high empirical success rates receive diminished gradient contributions, effectively shifting optimization pressure toward harder prompts where rare-correct modes are more likely to be underrepresented.

The scaled advantage is then defined as:

$$\widehat{A}_i^{\mathrm{F-GRPO}} := g(x) \cdot \widehat{A}_i^{\mathrm{GRPO}}$$AiF−GRPO​:=g(x)⋅AiGRPO​

This modification is algorithm-agnostic and can be directly integrated into any group-relative RLVR method. It requires no additional networks or parameters beyond the scalar hyperparameter $\gamma$γ, making it computationally lightweight. The authors demonstrate that this simple adjustment improves pass@256 across multiple baselines — GRPO, DAPO, and CISPO — while preserving or improving pass@1, validating that the method enhances solution diversity without sacrificing accuracy on common cases.

As shown in the figure below, the scaled advantage magnitude $g(x) \cdot |\widehat{A}^{\mathrm{GRPO}}|$g(x)⋅∣AGRPO∣ decreases as the success probability $\mu_{\mathrm{pos}}(x)$μpos​(x) increases, particularly for correct rollouts. This visualizes how F-GRPO suppresses updates on high-success prompts, redistributing gradient contribution toward more challenging cases where rare-correct trajectories are more likely to be missed.

Experiment

• Group size N in RL training exhibits three regimes: small N preserves diversity via infrequent updates, intermediate N causes distribution sharpening with peak tail-miss probability, and large N restores diversity through better coverage of rare correct modes.
• Focal weighting mitigates concentration in intermediate N regimes by suppressing updates on high-success prompts, improving pass@256 without sacrificing pass@1, and enhancing out-of-domain generalization.
• Empirical LLM results confirm the theoretical three-regime pattern: N=2 favors diversity, N=8 sharpens distribution, N=32 recovers diversity; Focal weighting at N=8 matches or exceeds N=32 performance with fewer rollouts.
• Focal weighting consistently improves pass@256 across multiple methods (GRPO, DAPO, CISPO) and model scales, often boosting out-of-domain pass@1, suggesting diversity preservation aids generalization.
• Focal weighting outperforms entropy and KL regularization in pass@1 and out-of-domain transfer, offering a simpler, more effective alternative for maintaining solution diversity.

The authors use focal weighting to modify group-relative policy optimization methods, finding that it consistently improves solution diversity (pass@256) across multiple models and benchmarks while maintaining or slightly improving single-attempt accuracy (pass@1). Results show that focal weighting mitigates the concentration of probability mass on common solutions, particularly at moderate group sizes where standard methods tend to sharpen the output distribution. This approach outperforms entropy and KL regularization in balancing accuracy and diversity, especially on out-of-domain tasks.

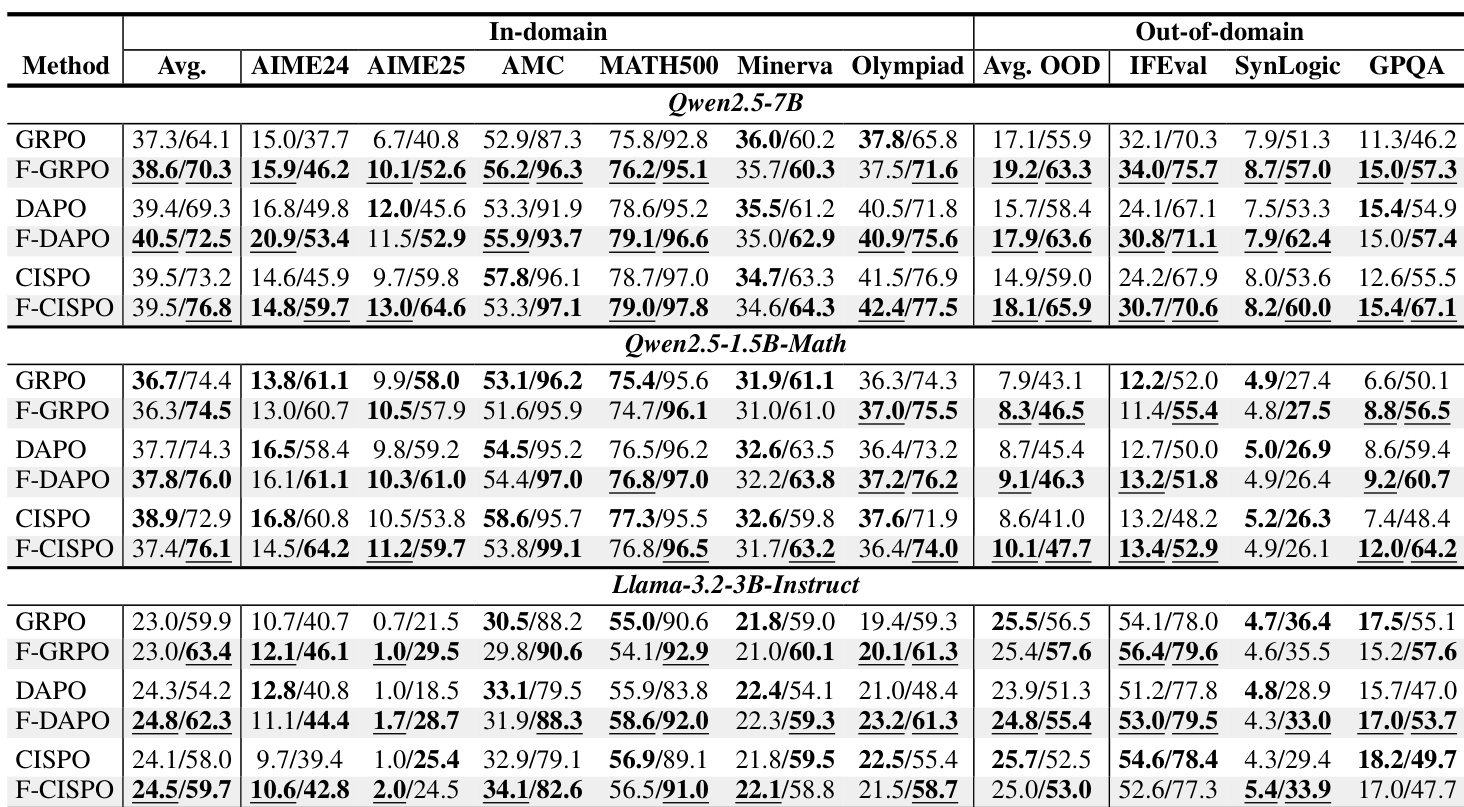
The authors use focal weighting to adjust gradient contributions during training, selecting γ values between 0.5 and 1.0 based on performance across models and methods. Results show that focal weighting consistently improves solution diversity (pass@256) while maintaining or slightly improving single-attempt accuracy (pass@1), particularly at commonly used group sizes like N=8. This approach mitigates the concentration of probability mass on a subset of solutions, preserving rare-correct modes without requiring additional rollout budget or complex regularization.

Results show that F-GRPO consistently improves out-of-domain pass@256 while maintaining or enhancing pass@1, outperforming both standard GRPO and KL-regularized variants. The method achieves this without increasing rollout cost, indicating that focal weighting effectively mitigates policy concentration on common solutions. This pattern holds across multiple benchmarks, suggesting broader generalization benefits from preserving solution diversity.

Results show that group size in GRPO training significantly affects solution diversity and accuracy, with intermediate sizes like N=8 causing the sharpest trade-off between pass@1 and pass@256 due to concentration on common solutions. Focal weighting at N=8 mitigates this by preserving rare-correct trajectories, achieving diversity comparable to larger groups while maintaining or improving single-attempt accuracy. The method also reduces deviation from base-model rare solutions, as reflected in lower ΔNLLrare values.

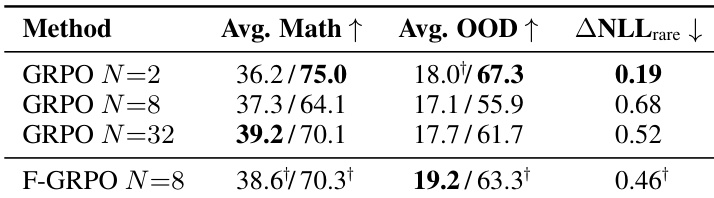
Results show that group size in GRPO training creates a trade-off between single-attempt accuracy and solution diversity, with intermediate sizes like N=8 often sharpening the policy at the cost of diversity, while smaller or larger sizes preserve broader solution coverage. Focal weighting at N=8 mitigates this sharpening, improving diversity metrics without sacrificing accuracy and matching or exceeding the performance of larger group sizes with fewer rollouts. This effect holds across in-domain and out-of-domain benchmarks, indicating that focal weighting helps retain rare correct solutions while maintaining or improving overall performance.