Command Palette
Search for a command to run...
MSign:安定ランク回復による大規模言語モデルの学習不安定を防止する最適化手法
MSign:安定ランク回復による大規模言語モデルの学習不安定を防止する最適化手法
Lianhai Ren Yucheng Ding Xiao Liu Qianxiao Li Peng Cheng Yeyun Gong
概要
大規模言語モデル(LLM)の事前学習における訓練不安定性は、依然として重要な課題であり、しばしば急激な勾配爆発として現れ、膨大な計算リソースを浪費する。本研究では、μPを用いてスケーリングされた500万パラメータのNanoGPTモデルにおける訓練失敗を分析し、崩壊に先立って生じる2つの重要な現象を特定した。すなわち、(1) 重み行列の安定ランク(フロベニウスノルムの二乗とスペクトルノルムの二乗の比)の急激な低下、および(2) 隣接層のヤコビアン間の整合性の増加である。理論的に、これらの2つの条件がネットワークの深さとともに勾配ノルムの指数関数的増大を引き起こすことを証明した。この不安定性メカニズムを打破するために、安定ランクを周期的に回復するための行列符号(matrix sign)操作を適用する新たな最適化手法MSignを提案する。500万~30億パラメータのモデルを対象とした実験により、MSignが訓練失敗を効果的に防止でき、計算オーバーヘッドは7.0%未満であることが示された。
One-sentence Summary
Researchers from Tsinghua University and Microsoft propose MSign, an optimizer using matrix sign operations to stabilize LLM training by restoring weight matrix stable rank, preventing gradient explosions in models from 5M to 3B parameters with under 7% overhead.
Key Contributions
- We identify stable rank collapse and growing Jacobian alignment as key precursors to training failure in LLMs, and prove that their combination triggers exponential gradient growth with network depth.
- We introduce MSign, an optimizer that periodically applies matrix sign operations to restore stable rank, thereby breaking the instability mechanism without disrupting training dynamics.
- Experiments across models from 5M to 3B parameters show MSign prevents gradient explosions with under 7.0% computational overhead, validating its effectiveness on both dense and MoE architectures.
Introduction
The authors leverage insights from matrix analysis and Jacobian dynamics to address training instability in large language models, a critical issue that wastes compute through unpredictable gradient explosions. Prior work often treats instability as a symptom—using clipping or scheduling—without targeting the root cause: the collapse of weight matrix stable rank and growing alignment between adjacent layer Jacobians, which together trigger exponential gradient growth. Their main contribution is MSign, an optimizer that periodically applies matrix sign operations to restore stable rank, thereby breaking the instability feedback loop. Validated across models from 5M to 3B parameters, MSign prevents failures with under 7% overhead and requires intervention only on attention projection layers.
Method
The authors leverage a theoretical framework to explain training instability in transformer models, centering on the interplay between stable rank collapse and Jacobian alignment. Their analysis begins with a standard decoder-only transformer architecture comprising L stacked blocks, each containing multi-head self-attention and position-wise MLP sublayers, with residual connections and LayerNorm. Hidden states H(ℓ−1)∈RT×d are transformed through linear projections WQ(ℓ),WK(ℓ),WV(ℓ),WO(ℓ) for attention, and W1(ℓ),W2(ℓ) for the MLP. The layer-wise transformation is denoted as H(ℓ)=F(ℓ)(H(ℓ−1)), and the layer Jacobian is defined as J(ℓ)=∂vec(H(ℓ−1))∂vec(H(ℓ)).
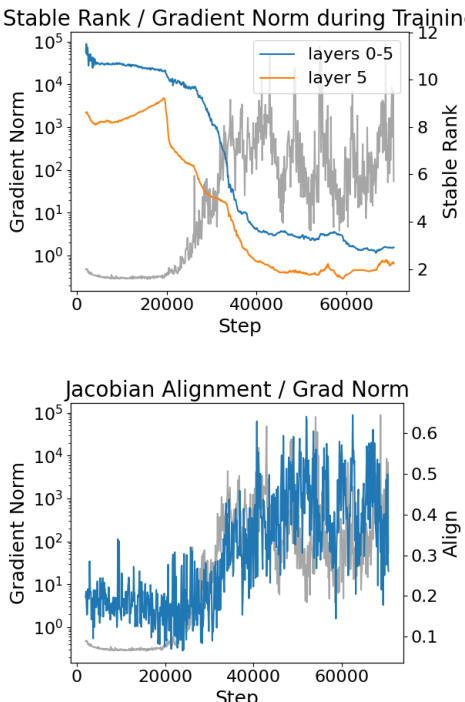
The core failure mechanism is formalized as a causal chain: low stable rank and high Jacobian alignment lead to exponentially growing total Jacobian norms, which in turn induce large weight gradients and training instability. The stable rank of a matrix W, defined as srank(W)=∥W∥22∥W∥F2, quantifies how evenly energy is distributed across singular values. For linear layers, Theorem 4.4 establishes that under fixed Frobenius norm, the operator norm ∥W∥2 scales inversely with the square root of stable rank: ∥W∥2=srank(W)∥W∥F. This relationship extends to attention and MLP layers: for attention, the Jacobian norm is bounded by terms involving ∥WV∥2∥WO∥2, and for MLPs, by srank(W1)⋅srank(W2)Lϕ∥W1∥F∥W2∥F, where Lϕ is the Lipschitz constant of the activation. Thus, across all layer types, low stable rank amplifies layer Jacobian norms.
Jacobian alignment, defined as the cosine similarity between the top right singular vector of J(ℓ) and the top left singular vector of J(ℓ+1), suppresses cancellation in matrix products. Theorem 4.2 provides a lower bound on the total Jacobian norm: if each ∥J(ℓ)∥2≥M and alignment ≥a>0, then ∥Jtotal∥2≥a(aM)L. When aM>1, this bound grows exponentially with depth L, explaining the observed gradient explosion. This condition is empirically met during failure regimes, where stable rank collapse elevates M and alignment a increases.
The final link in the chain connects total Jacobian norm to weight gradient magnitude. Theorem 4.8 shows that under gradient alignment assumptions — including alignment between local gradients and Jacobian singular directions — the gradient norm for weights at layer i is bounded below by aγ(aM)L−i⋅∂h(L)∂L2, where γ is a uniform lower bound on local gradient norms. Summing over all layers, Theorem 4.9 yields a total gradient norm lower bound that grows as (aM)2−1(aM)2L−1, again exponential in depth when aM>1.
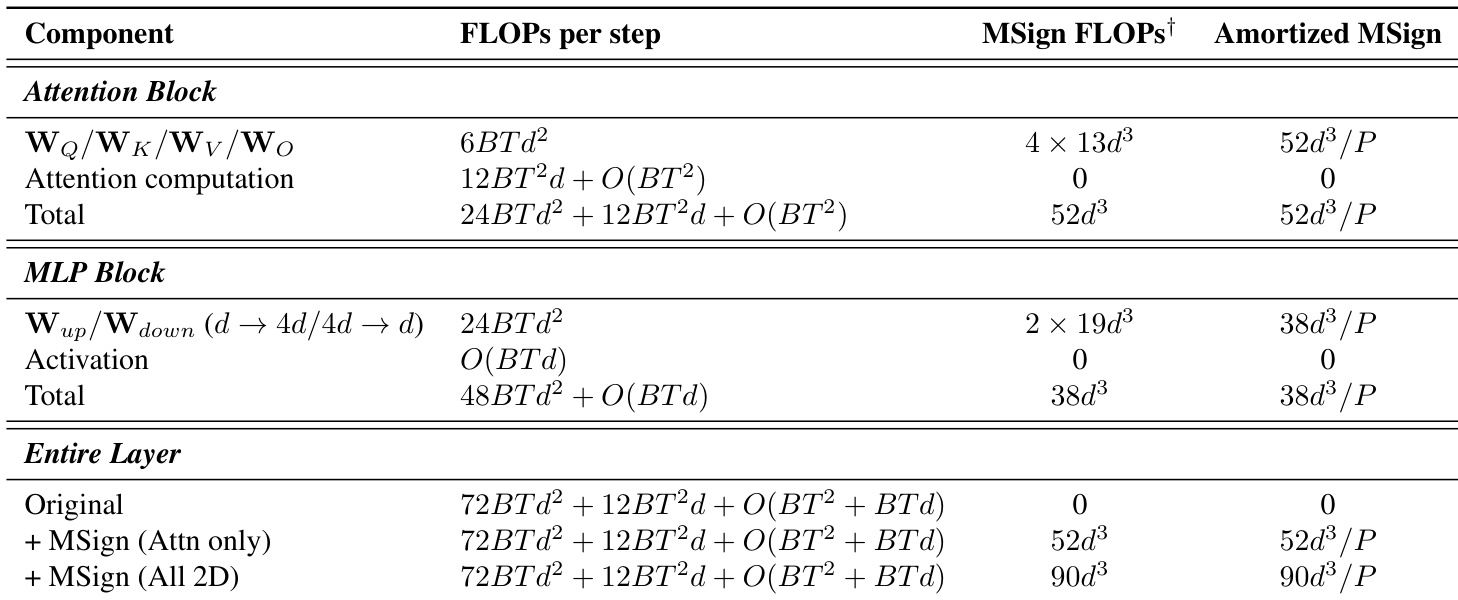
To break this feedback loop, the authors propose the MSign optimizer. It periodically applies the matrix sign operation — defined via SVD as sign(W)=UVT — to restore stable rank by setting all non-zero singular values to 1. To preserve scale, the result is rescaled to match the original Frobenius norm: Wnew=∥sign(W)∥F∥W∥Fsign(W). In practice, MSign is applied every P steps (e.g., P=100) and can be targeted to specific layers such as attention projections or all 2D parameters, reducing computational cost while maintaining efficacy. This intervention prevents stable rank collapse and stabilizes training across model scales, as validated empirically.
Experiment
- Training failures in transformers under moderate learning rates are preceded by two consistent phenomena: sharp decline in weight stable rank and increasing Jacobian alignment between adjacent layers, both correlating with gradient explosion.
- MSign effectively prevents training collapse across diverse model scales and architectures, including MoE, by maintaining bounded gradient norms and stable loss trajectories.
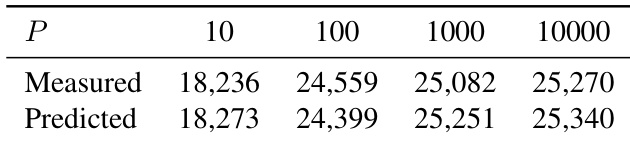
- MSign’s computational overhead is theoretically minimal (<0.1%) but practically higher (4–7%) due to distributed SVD communication and kernel fusion disruption, though still modest compared to failure-related waste.
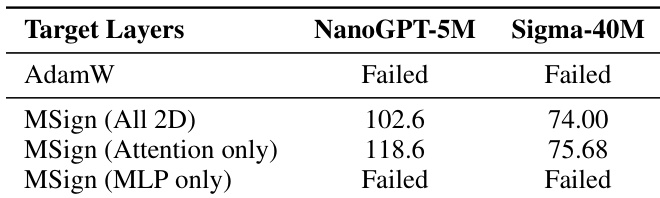
- Ablation studies confirm MSign must target attention layers to prevent collapse; applying it to all 2D parameters further improves final model quality.
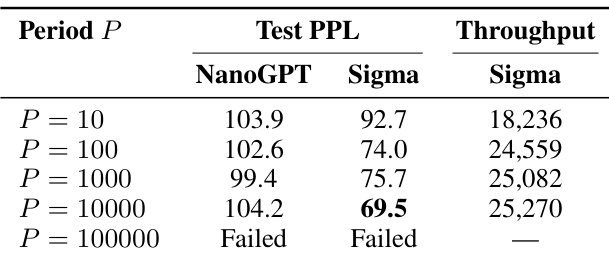
- MSign remains effective across application periods from 10 to 10,000 steps, but periods ≥1000 introduce instability; P=100 is recommended for optimal stability and acceptable overhead.
The authors use MSign to stabilize transformer training across multiple model scales, preventing gradient explosion and loss divergence while maintaining throughput. Although theoretical overhead is negligible, measured overhead ranges from 4.6% to 6.7% due to implementation bottlenecks like distributed SVD synchronization and kernel fusion disruption. Results show MSign consistently prevents training collapse regardless of model size or architecture, with attention layers being critical for its effectiveness.

The authors use MSign to stabilize transformer training by periodically constraining weight matrices, which prevents gradient explosion and training collapse without requiring architectural changes. Results show that applying MSign to attention layers alone is sufficient to maintain stability, while including MLP layers further improves final model quality, and the computational overhead remains modest even when applied to all 2D parameters.
The authors use MSign to stabilize transformer training by periodically controlling weight matrix properties, finding that application periods from 10 to 10,000 steps all prevent collapse but longer intervals introduce transient instability. Results show that while throughput predictions based on FLOPs are optimistic, real-world overhead stems from communication and kernel fusion disruptions, yet remains modest compared to failure costs. The recommended P=100 balances stability and efficiency, maintaining low gradient norms and smooth loss trajectories across model scales.
The authors use MSign to stabilize transformer training by targeting specific layers, finding that applying it only to attention layers prevents collapse while MLP-only application fails. Results show that applying MSign to all 2D parameters yields the best final model quality, confirming attention layers as the primary source of instability.
The authors evaluate MSign’s effectiveness across different application periods and find that while training remains stable for periods up to 10,000 steps, longer intervals lead to failure, indicating a critical threshold for intervention frequency. Results show that shorter periods like P=100 yield the best balance between model quality and throughput, with P=10000 already showing signs of instability despite eventual convergence. Throughput remains relatively stable across tested periods, but the risk of collapse increases sharply beyond P=10,000, underscoring the need for timely intervention to maintain training stability.