Command Palette
Search for a command to run...
難易度認識型GRPOと多面的質問再構成を活用した数学的推論の向上
難易度認識型GRPOと多面的質問再構成を活用した数学的推論の向上
Yanqi Dai Yuxiang Ji Xiao Zhang Yong Wang Xiangxiang Chu Zhiwu Lu
概要
検証可能な報酬を用いた強化学習(Reinforcement Learning with Verifiable Rewards: RLVR)は、大規模モデルにおける数学的推論能力を強化するための堅牢な手法を提供する。しかしながら、既存の手法は、未発達な能力の洗練に不可欠であるにもかかわらず、アルゴリズム的およびデータ的視点の両面から、より困難な問題に対する配慮が系統的に欠如していることを指摘する。アルゴリズム的に見て、広く用いられているグループ相対的方策最適化(Group Relative Policy Optimization: GRPO)は、難易度の高い問題に対して方策更新の大きさが低くなるという内包的な不均衡を抱えている。データ的視点では、拡張手法が主に問題文の言い換えによって多様性を高めるにとどまり、本質的な難易度を体系的に向上させるものではない。こうした課題に対処するため、本研究では、アルゴリズム的およびデータ的両面から困難な問題に焦点を当てることで数学的推論能力を向上させる「二重双対型」のMathForgeフレームワークを提案する。このフレームワークは、難易度に配慮したグループ方策最適化(Difficulty-Aware Group Policy Optimization: DGPO)アルゴリズムと、複数の側面から問題を再構成する多面的問題再表現(Multi-Aspect Question Reformulation: MQR)戦略から構成される。具体的には、DGPOは難易度に応じたグループアドバンテージ推定によりGRPOの内包的な不均衡を修正し、さらに難易度に応じた問題レベルの重み付けにより困難な問題を優先的に処理する。一方、MQRは問題の難易度を向上させつつも、元の正解(gold answer)を保持するように複数の側面から問題を再表現する。全体として、MathForgeは相乗的なサイクルを形成する:MQRがデータの境界を拡張し、DGPOが拡張されたデータから効果的に学習する。広範な実験により、MathForgeがさまざまな数学的推論タスクにおいて既存手法を顕著に上回ることを示した。コードおよび拡張データはすべて、https://github.com/AMAP-ML/MathForge で公開されている。
One-sentence Summary
Researchers from Renmin University, Alibaba, Xiamen, and Dalian Universities propose MathForge—a dual framework combining DGPO and MQR—to enhance mathematical reasoning in LLMs by prioritizing harder questions via difficulty-aware policy updates and multi-aspect reformulation, outperforming prior methods across benchmarks.
Key Contributions
- We identify and correct a critical imbalance in Group Relative Policy Optimization (GRPO) through Difficulty-Aware Group Policy Optimization (DGPO), which normalizes advantage estimation by mean absolute deviation and weights harder questions more heavily to focus training on solvable weaknesses.
- We introduce Multi-Aspect Question Reformulation (MQR), a data augmentation strategy that systematically increases question difficulty by reformulating problems across multiple dimensions—such as adding story context or nesting sub-problems—while preserving the original gold answer to maintain verifiability.
- MathForge, combining DGPO and MQR, achieves state-of-the-art performance across multiple mathematical reasoning benchmarks, demonstrating significant gains over existing RLVR methods and validating its effectiveness through extensive experiments on diverse models.
Introduction
The authors leverage reinforcement learning with verifiable rewards (RLVR) to improve mathematical reasoning in large language models, a method that avoids costly neural reward models by using rule-based scoring. However, existing approaches like Group Relative Policy Optimization (GRPO) unintentionally suppress updates on harder questions due to an imbalance in advantage estimation, while data augmentation methods focus on diversity without systematically increasing difficulty. To fix this, they introduce MathForge—a dual framework combining Difficulty-Aware Group Policy Optimization (DGPO), which rebalances update magnitudes and weights harder questions more heavily, and Multi-Aspect Question Reformulation (MQR), which augments data by reformulating questions to increase difficulty across story, terminology, and sub-problem dimensions—all while preserving the original correct answer. Their approach creates a synergistic loop where harder, reformulated data trains a model that better targets its weaknesses, yielding state-of-the-art results across benchmarks.
Dataset
- The authors use MQR-augmented data derived from the public MATH dataset, reformulating existing problems to enhance mathematical reasoning tasks.
- No personally identifiable or sensitive information is included, ensuring privacy compliance and alignment with the ICLR Code of Ethics.
- The dataset supports training models focused on advancing AI capabilities in math, with potential applications in science, engineering, and education.
- No cropping, metadata construction, or additional processing beyond problem reformulation is described in this section.
Method
The authors leverage a modified policy optimization framework to enhance mathematical reasoning in language models, building upon Group Relative Policy Optimization (GRPO) and introducing two core components: Difficulty-Aware Group Policy Optimization (DGPO) and Multi-Aspect Question Reformulation (MQR). The overall training process operates within a batched setting where queries are sampled from a dataset D, and multiple responses {osi} are generated using an old policy πθold. Each response is assigned a scalar reward rsi, typically based on correctness, forming a reward distribution per query. The policy model πθ is then updated using a token-level objective that incorporates relative advantages estimated within each group of responses to the same query.
[[IMG:|Framework diagram]]
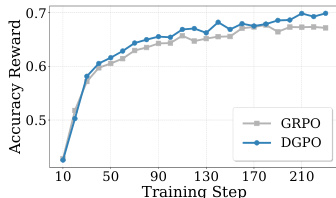
The core of the method, DGPO, addresses a fundamental imbalance in GRPO's optimization objective. GRPO uses group relative advantage estimation (GRAE), where the advantage A^GR,i for a response oi is computed as the normalized difference between its reward ri and the mean reward of the group, scaled by the standard deviation. This normalization leads to a total update magnitude for a single question that depends on the accuracy rate p, peaking at p=0.5 and diminishing for easier or harder questions. This imbalance is problematic because challenging questions, even with non-zero accuracy, are crucial for targeted learning and model improvement. To resolve this, DGPO introduces Difficulty-Balanced Group Advantage Estimation (DGAE), which replaces the standard deviation in the denominator with the mean absolute deviation (MAD) of the rewards. This change ensures that the total update magnitude for any question becomes a constant value G, independent of the accuracy rate, thereby balancing the influence of all questions regardless of their difficulty.
Furthermore, DGPO employs Difficulty-Aware Question-Level Weighting (DQW) to explicitly prioritize more challenging questions. This is achieved by assigning a weight λs to each query qs in the batch, computed as a softmax over the negative mean reward of its responses, scaled by a temperature hyperparameter T. Queries with lower average rewards (i.e., harder questions) receive higher weights, increasing their contribution to the overall loss. The final DGPO objective combines these elements, using the DGAE advantage A^DG,si and the DQW weight λs in a clipped policy gradient loss, while averaging the loss over valid tokens from valid queries to ensure training stability.
Complementing the algorithmic improvements, the MQR strategy provides a data-centric enhancement. It automatically reformulates existing questions using a large reasoning model to generate more complex variants that preserve the original answer. This is achieved through three methods: adding a story background to introduce noise, inventing abstract mathematical terms to test conceptual understanding, and converting key numerical conditions into independent sub-problems to enforce multi-step reasoning. The resulting augmented dataset, combining original and reformulated questions, provides a richer and more challenging training environment for the policy model, creating a synergistic loop where improved data enables better learning, and better learning allows the model to tackle more complex reformulations.
Experiment
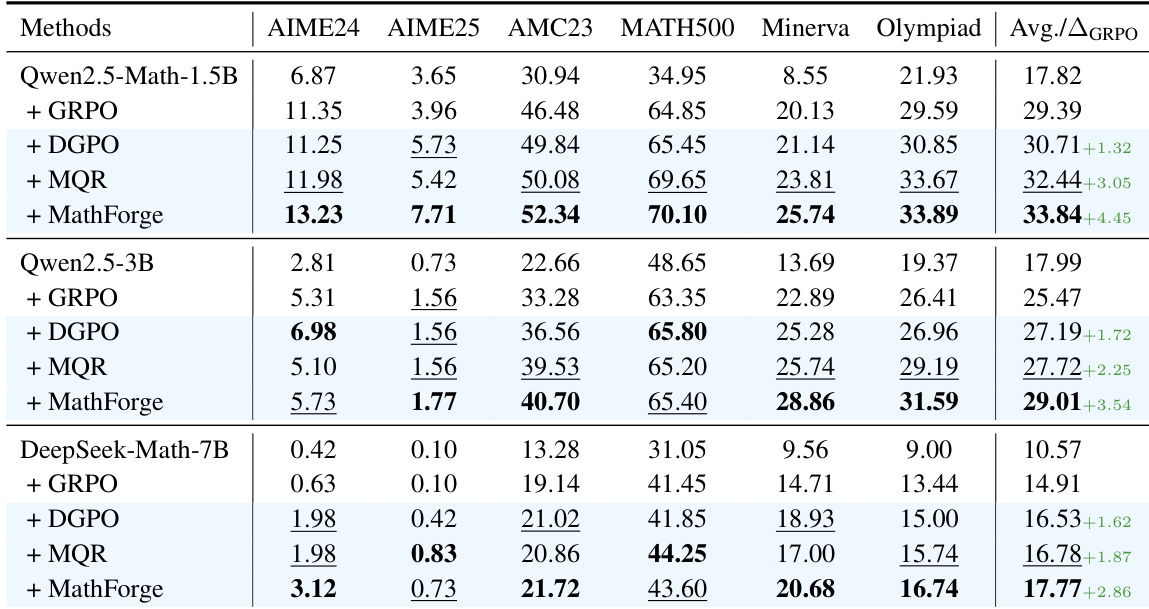
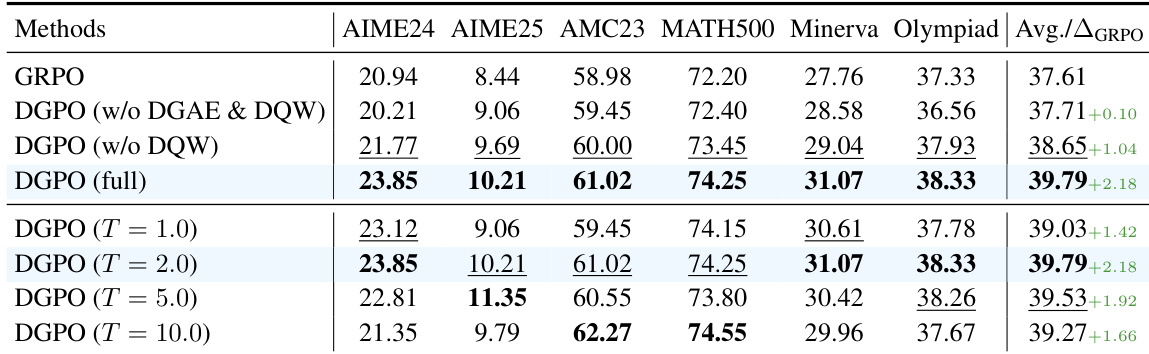
- DGPO alone improves Qwen2.5-Math-7B’s MATH average score to 39.79% (vs. 37.61% for GRPO), validating difficulty-aware policy optimization via DGAE and DQW.
- MQR boosts performance to 41.04% by augmenting data with narrative, abstract, and nested-logic reformulations, proving data diversity enhances reasoning robustness.
- MathForge (DGPO + MQR) achieves 42.17% on MATH, demonstrating synergy: MQR supplies challenging data, DGPO prioritizes learning on weaknesses.
- MathForge generalizes across models (Qwen2.5-Math-1.5B, 3B, DeepSeek-Math-7B), consistently outperforming baselines, confirming model-agnostic effectiveness.
- In multimodal domain, DGPO on Qwen2.5-VL-3B-Instruct achieves 59.95% on GEOQA-8k (vs. 57.43% for GRPO), proving cross-domain applicability.
- Ablations show DGPO components contribute cumulatively: DGAE (+0.94%), DQW (+1.14%); MQR’s three strategies synergize, outperforming individual or MetaMath-Rephrasing baselines.
- MQR’s reformulated questions are harder (72.04% accuracy on Sub-Problem vs. 79.77% on Original), yet training on them yields better generalization (“train harder, test better”).
- Even smaller reformulators (Qwen2.5-7B, Qwen3-30B) deliver gains, showing MQR’s low dependency on reformulator capability.
- DGPO integrates with GPG, DAPO, GSPO, further improving performance (e.g., DAPO+DGPO: 39.91%), confirming its compatibility as a general enhancement module.
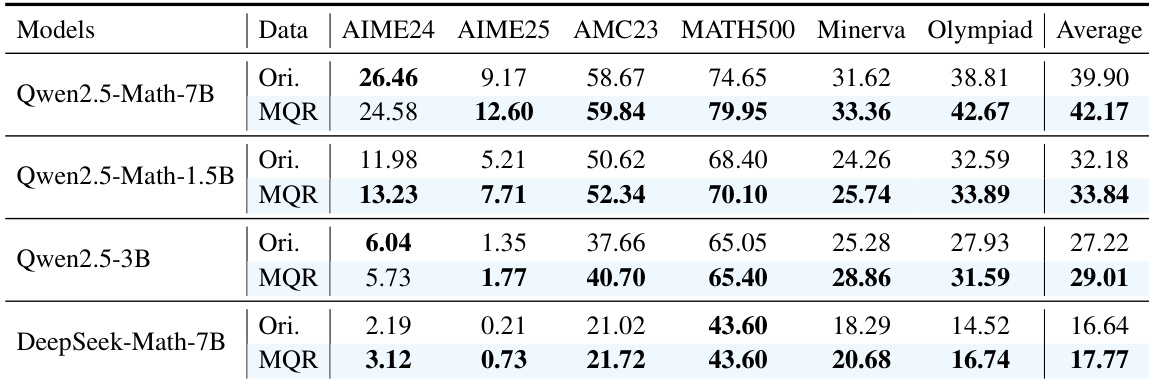
The authors use the Qwen2.5-Math-7B model to evaluate the effectiveness of their MathForge framework, which combines DGPO and MQR. Results show that MathForge achieves the highest average performance across all benchmarks, outperforming both individual components and the GRPO baseline, with a significant improvement of 4.45% over GRPO.
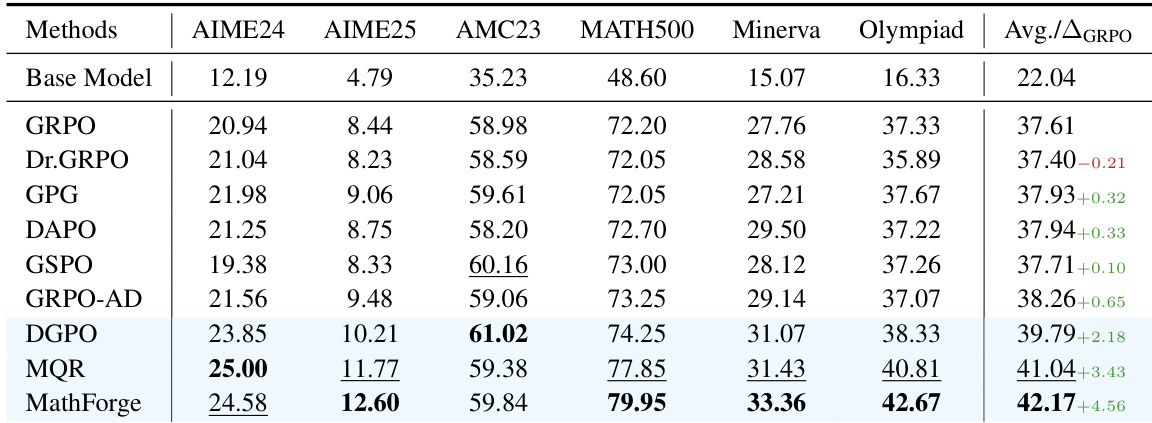
The authors use the Qwen2.5-VL-3B-Instruct model to evaluate the DGPO algorithm in the multimodal domain on the GEOQA-8k dataset. Results show that DGPO achieves the highest performance of 59.95%, significantly outperforming the GRPO baseline at 57.43%.

The authors use the Qwen2.5-Math-7B model to evaluate various reinforcement learning methods on the MATH dataset, with results showing that MathForge achieves the highest average performance across all benchmarks. Results show that MathForge outperforms all individual components and baselines, reaching an average score of 42.17%, which is a significant improvement over the GRPO baseline of 37.61%.
The authors use DGPO with different temperature settings to analyze the impact of question difficulty weighting on model performance. Results show that setting the temperature to 2.0 achieves the highest average score of 39.79%, outperforming both lower and higher temperature settings, indicating that this value optimally balances the prioritization of challenging questions while maintaining learning from the entire batch.
The authors use the Qwen2.5-Math-7B model to evaluate the effectiveness of MathForge on the MATH dataset, comparing performance between original data and MQR-augmented data across multiple benchmarks. Results show that MQR consistently improves average performance over the original data, with the Qwen2.5-Math-7B model achieving an average score of 42.17% on MQR-augmented data, significantly higher than the 39.90% on original data.