One-sentence Summary

Researchers from Renmin University of China propose DARC, a two-stage self-play framework that decouples question generation and solver training to stabilize LLM self-improvement, using difficulty-calibrated prompts and asymmetric distillation, achieving 10.9-point gains across benchmarks without human labels.

Key Contributions

• DARC addresses optimization instability in LLM self-play by decoupling Questioner and Solver training, replacing solver-dependent rewards with explicit difficulty calibration and external corpora to stabilize question generation.
• It introduces an asymmetric self-distillation mechanism where a document-augmented teacher generates high-quality pseudo-labels to supervise a student Solver without document access, reducing bootstrapping errors and self-confirmation bias.
• Evaluated across nine reasoning benchmarks and three backbone models, DARC delivers a 10.9-point average improvement over baselines and matches fully supervised performance without human annotations.

Introduction

The authors leverage self-play to enable large language models to evolve without human supervision, a critical step toward scalable, general AI. Prior self-play methods suffer from unstable optimization due to non-stationary rewards and error amplification from self-generated pseudo-labels, often leading to performance collapse. DARC addresses this by decoupling the process into two stages: first training a Questioner to generate difficulty-calibrated questions using external corpora, then training a Solver via asymmetric self-distillation where a document-augmented teacher provides cleaner pseudo-labels for a student that lacks document access. This design yields model-agnostic gains of 10.9 points on average across nine reasoning benchmarks and rivals fully supervised models—without using any human annotations.

Dataset

• The authors use only publicly available datasets, including DataComp-LM and Nemotron-CC-Math, with no collection of user data.
• These corpora are pre-curated and filtered by their original creators to reduce personally identifying information and offensive content; the authors rely on those procedures without additional filtering.
• The datasets are used in an offline experimental setting for model self-evolution research, not for real-world deployment or autonomous decision-making.
• Raw training text is not released, and no individual-level analysis is performed; results are reported only in aggregated form.
• ChatGPT was used exclusively for language editing and clarity improvements, not for scientific design, analysis, or interpretation.

Method

The DARC framework decomposes the self-evolution of large language models into two distinct, sequentially executed stages: Questioner training and Solver training. This decoupled approach aims to stabilize the optimization process by separating the generation of a reasoning curriculum from the training of the solving capability. The overall architecture is illustrated in the framework diagram, which contrasts the unstable dynamics of previous methods with the structured, two-phase DARC process.

In the first stage, the Questioner is trained to generate questions that are both grounded in a source document and calibrated to a specified difficulty level. The Questioner, parameterized as $\mathcal{Q}_{\theta}$Qθ​, takes as input a document $d$d and a target difficulty scalar $\tau \in [0,1]$τ∈[0,1], and generates a question $q$q conditioned on these inputs. To train this model, the authors employ Group Relative Policy Optimization (GRPO) with a reward function designed to enforce both document grounding and difficulty alignment. The reward for a generated question $q$q is computed in two stages. First, an LLM-as-a-Judge evaluates whether $q$q is grounded in the source document $d$d; ungrounded questions receive a negative reward of $-1$−1. For grounded questions, the empirical difficulty is estimated using a fixed Solver model, $\mathcal{S}(\cdot \mid q)$S(⋅∣q), by sampling $N$N candidate answers and calculating the success rate, $\hat{s} = \frac{1}{N} \sum_{j=1}^{N} \mathbb{I}[\hat{a}_j = a^*]$s^=N1​∑j=1N​I[a^j​=a∗], where $a^*$a∗ is the pseudo-label obtained via majority voting. This success rate serves as the difficulty estimator $D(q)$D(q). The final reward is then defined as $r_Q(q) = 1 - |D(q) - \tau|$rQ​(q)=1−∣D(q)−τ∣ for grounded questions, which encourages the Questioner to produce questions whose estimated difficulty matches the target $\tau$τ. This process is visualized in the upper portion of the detailed architecture diagram, showing the Questioner generating questions, the Solver providing answers for difficulty estimation, and the reward calculation feeding back into the policy update.

The second stage involves training the Solver using the offline curriculum constructed by the trained Questioner. The Questioner's parameters are frozen, and it is used to generate a set of questions $\mathcal{U} = \{(d_i, \tau_i, q_i)\}_{i=1}^M$U={(di​,τi​,qi​)}i=1M​, where $q_i \sim \mathcal{Q}_{\theta}(\cdot \mid d_i, \tau_i)$qi​∼Qθ​(⋅∣di​,τi​). These questions are ordered by their specified difficulty level $\tau_i$τi​ to form a curriculum, which is used to train the Solver progressively from easy to hard. To obtain supervision without external annotations, the framework employs asymmetric self-distillation. For each question $q$q in the curriculum, a privileged teacher Solver, which has access to the source document $d$d, generates multiple candidate answers $\{\hat{a}_1^{(d)}, \ldots, \hat{a}_N^{(d)}\}${a^1(d)​,…,a^N(d)​}. A pseudo-label $a^*$a∗ is derived via majority voting over these answers, and samples with low agreement are discarded. The student Solver, $\mathcal{S}_\phi(\cdot \mid q)$Sϕ​(⋅∣q), which does not have access to $d$d, is then trained to generate answers to the question $q$q alone. The training objective for the student is to maximize the correctness reward, $r_S(a) = \mathbb{I}[a = a^*]$rS​(a)=I[a=a∗], where $a$a is a sample from the student's output distribution. This asymmetry prevents the student from simply copying from the document and forces it to learn to solve problems based solely on the question. The detailed architecture diagram illustrates this process, showing the generation of questions, the role of the privileged teacher, the creation of pseudo-labels, and the training of the student Solver. The framework's design, as shown in the diagram, ensures that the Questioner is trained on a stationary objective, while the Solver is trained on a stable, externally defined curriculum, thereby mitigating the optimization instability inherent in coupled self-play systems.

Experiment

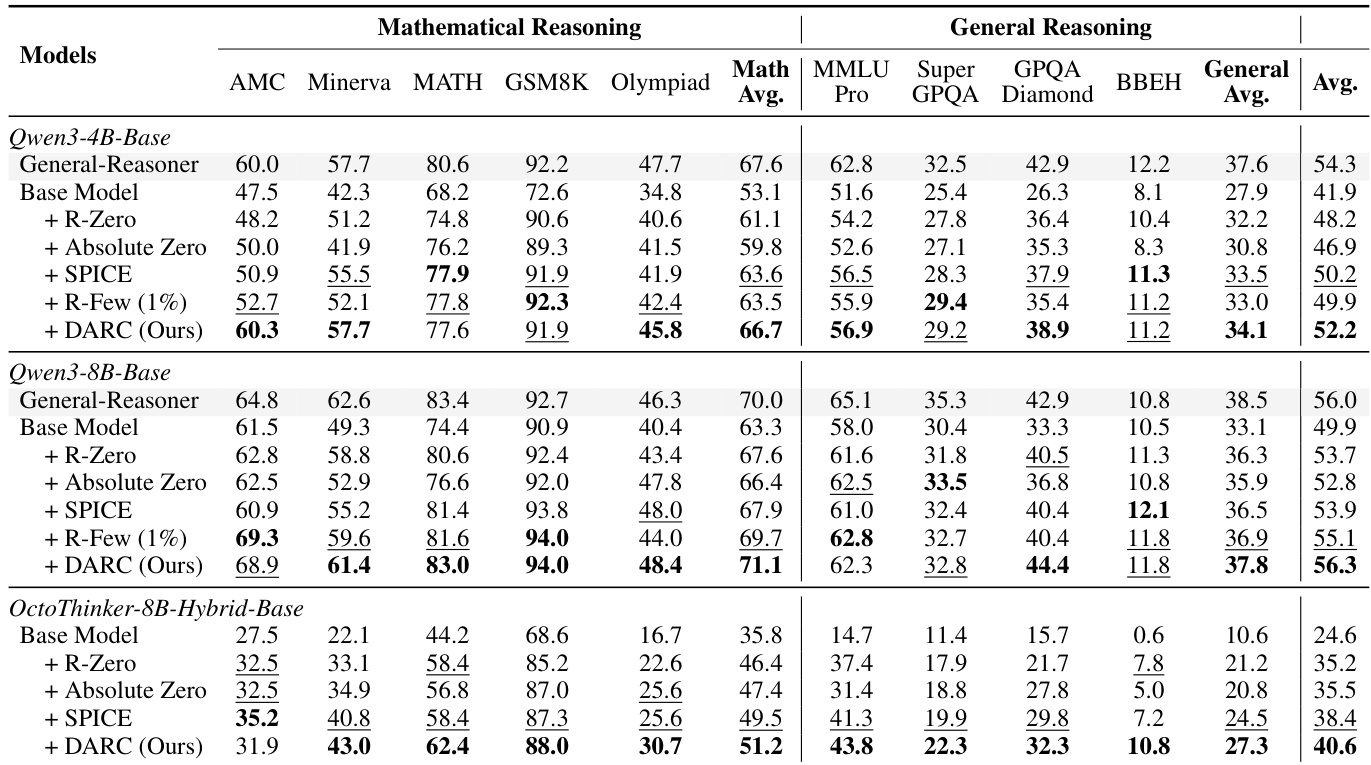
• Evaluated DARC across Qwen3-4B/8B and OctoThinker-8B backbones, outperforming label-free baselines (R-Zero, Absolute Zero, SPICE) and matching weakly supervised R-Few without human annotations; achieved 10.9-point avg gain over base models.
• On math benchmarks (MATH-500, GSM8K, etc.) and general reasoning (MMLU-Pro, GPQA-Diamond, etc.), DARC showed strongest gains on weaker models and math tasks, with Qwen3-8B matching supervised General-Reasoner’s performance.
• Training dynamics confirmed stable optimization: reward rose steadily with curriculum transitions; validation reward improved without collapse, unlike prior self-play systems.
• Asymmetric distillation with document grounding improved performance (Avg@8 win rates >50% for short/medium contexts), though gains faded beyond 5K tokens due to noise.
• Questioner generated solver-agnostic, difficulty-graded questions; cross-solver generalization validated using Qwen3-4B Questioner to train 1.7B and 8B Solvers with consistent gains.
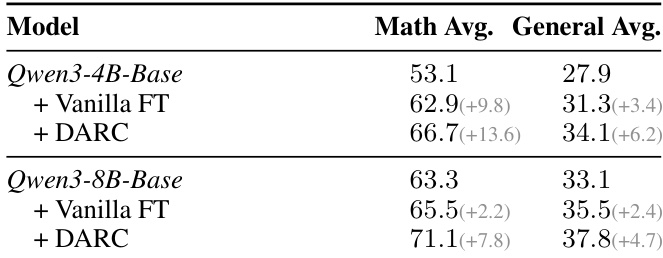
• DARC outperformed vanilla fine-tuning by 3.3–3.9 points across scales, proving it enhances reasoning beyond corpus memorization.
• Ablations confirmed necessity of asymmetric distillation, specialized Questioner, and difficulty-aware curriculum; replacing Questioner with generic model degraded results.

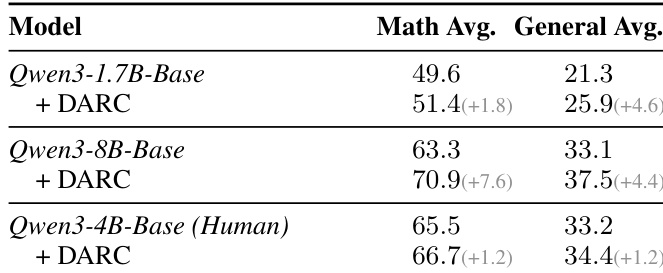
The authors use DARC to evaluate its effectiveness on different model scales, showing that it consistently improves performance across all backbones. Results show that DARC achieves significant gains on both mathematical and general reasoning benchmarks, with the largest improvements observed on smaller models like Qwen3-1.7B and Qwen3-4B, where it outperforms the base models by 1.8 and 1.2 points in math and general reasoning, respectively.

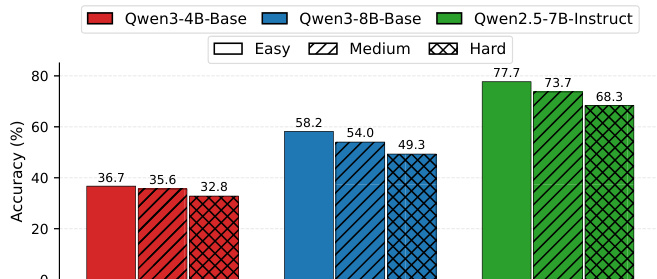
The authors use a trained Questioner to generate questions of varying difficulty levels and evaluate the resulting Solver accuracy across different model scales. Results show that Solver accuracy decreases monotonically from Easy to Hard across all models, indicating that the Questioner learns a solver-agnostic and input-driven difficulty partition.

The authors use DARC to improve reasoning performance on mathematical and general benchmarks, showing that DARC consistently outperforms base models and label-free baselines across both Qwen3-4B and Qwen3-8B backbones. Results show that DARC achieves higher average scores than Vanilla FT on both math and general reasoning, with larger gains on the 8B model, indicating that DARC more effectively transfers reasoning capabilities beyond simple corpus memorization.

The authors compare the performance of Qwen3-4B-Base and Qwen2.5-7B-Instruct on reasoning tasks across different document lengths, with Qwen2.5-7B-Instruct achieving higher scores in short and medium contexts while both models show lower performance in long contexts. Results indicate that instruction tuning improves reasoning ability, particularly in shorter contexts, but gains diminish as document length increases, likely due to noise from excessive information.

The authors use DARC to evaluate its performance on mathematical and general reasoning benchmarks across three model scales, showing that DARC consistently outperforms label-free baselines and achieves competitive results with weakly supervised methods. Results show that DARC improves average scores by 10.9 points over base models and matches the performance of the supervised General-Reasoner on Qwen3-8B, indicating that self-evolution can achieve strong reasoning capabilities without human annotations.