Command Palette
Search for a command to run...
レアなものを報酬する:LLMにおける創造的問題解決のための独自性認識型RL
レアなものを報酬する:LLMにおける創造的問題解決のための独自性認識型RL
Zhiyuan Hu Yucheng Wang Yufei He Jiaying Wu Yilun Zhao See-Kiong Ng Cynthia Breazeal Anh Tuan Luu Hae Won Park Bryan Hooi
概要
強化学習(RL)は、特に複雑な推論タスクにおいて、事後訓練段階での大規模言語モデル(LLM)の中心的な枠組みとして広く採用されているが、しばしば「探索の崩壊(exploration collapse)」という問題に直面する。すなわち、ポリシーが早期に少数の優勢な推論パターンに集中し、pass@1の性能は向上するものの、ロールアウトレベルでの多様性やpass@kの向上が制限される。本研究では、この問題の根本原因が、解の集合全体の多様性ではなく、局所的なトークン行動の正則化に起因していると主張する。これを解決するため、我々は「ユニークネス認識型強化学習(Uniqueness-Aware Reinforcement Learning)」を提案する。この手法は、ロールアウトレベルの目的関数に基づき、高レベルの戦略として希少性を持つ正しい解を明示的に報酬づける。本手法では、LLMを用いたジャッジが、同一問題に対する複数のロールアウトを、表面的な差異を無視して高レベルの解決戦略に基づいてクラスタリングし、クラスタのサイズに反比例するようにポリシーの利得を再重み付けする。その結果、既存のものとは異なる新しい戦略を用いた正解は、重複する戦略よりも高い報酬を得るようになる。数学、物理学、医学推論のベンチマークにおいて、本手法は大規模なサンプリングバジェット下でもpass@kを一貫して向上させ、pass@1の性能を損なうことなくpass@k曲線下の面積(AUC@K)を増加させ、スケールに応じた探索の維持とより多様な解決戦略の発見を実現した。
One-sentence Summary
The authors, affiliated with MIT, NUS, Yale, and NTU, propose Uniqueness-Aware Reinforcement Learning, a rollout-level objective that rewards rare high-level reasoning strategies via LLM-based clustering and inverse cluster-size reweighting, improving solution diversity and pass@k performance across mathematics, physics, and medical reasoning benchmarks without sacrificing pass@1.
Key Contributions
- Reinforcement learning for large language models often suffers from exploration collapse, where policies converge to a narrow set of dominant reasoning patterns, limiting solution diversity despite improvements in pass@1; this work identifies the root cause as the misalignment between token-level regularization and the need for strategy-level diversity in complex reasoning tasks.
- The authors propose Uniqueness-Aware Reinforcement Learning, a rollout-level objective that uses an LLM-based judge to cluster solutions by high-level strategy, reweighting policy advantages inversely with cluster size to reward rare, correct solution paths while downweighting redundant ones.
- Evaluated on mathematics, physics, and medical reasoning benchmarks, the method consistently improves pass@k across large sampling budgets and increases AUC@k without sacrificing pass@1, demonstrating enhanced exploration and broader coverage of human-annotated solution strategies.
Introduction
Reinforcement learning (RL) for post-training large language models (LLMs) is critical for enhancing complex reasoning, but it often suffers from exploration collapse—where policies converge to a narrow set of dominant reasoning patterns, improving pass@1 while failing to boost pass@k due to insufficient diversity in solution strategies. Prior methods attempt to address this through token-level diversity signals like entropy bonuses or embedding distances, but these fail to capture high-level strategic differences, treating superficial variations as meaningful diversity. The authors introduce Uniqueness-Aware Reinforcement Learning, a rollout-level objective that uses an LLM-based judge to cluster multiple solution attempts by their high-level strategies, then reweights policy advantages inversely with cluster size. This rewards correct, rare strategies while downweighting common ones, promoting genuine strategy-level diversity. Evaluated across mathematics, physics, and medical reasoning benchmarks, the method consistently improves pass@k and AUC@k without sacrificing pass@1, enabling sustained exploration even at large sampling budgets.
Dataset
- The dataset comprises domain-specific reasoning problems from three disciplines: mathematics, physics, and medicine, curated for reinforcement learning (RL) training.
- For mathematics, the authors use a difficulty-filtered subset of MATH (Hendrycks et al., 2021), selecting 8,523 problems from Levels 3–5—representing harder, more complex questions—suitable for advanced reasoning tasks.
- In physics, the dataset is derived from the textbook reasoning split of MegaScience (Fan et al., 2025), with 7,000 examples randomly sampled from a pool of 1.25 million textbook-based items to ensure broad coverage of conceptual reasoning.
- For medicine, 3,000 examples are randomly selected from MedCaseReasoning (Wu et al., 2025), which contains 13.1k total cases, focusing on clinical reasoning scenarios relevant to diagnostic decision-making.
- The training process uses these subsets with a fixed mixture ratio across domains, combining them into a unified training mix to support multi-domain reasoning.
- Each training example is processed with standardized formatting, including structured prompts and ground truth answers, and is used in rollout-based RL training with 8 rollouts per prompt.
- The authors apply a cropping strategy to limit generation length: 4096 new tokens for Qwen-2.5 and 20480 for Qwen-3 and OLMo-3 models, ensuring efficient training while preserving context.
- Metadata for each example includes domain, problem type, and difficulty level, constructed from source annotations and used to guide training and evaluation.
- The models are trained using AdamW with a learning rate of 5×10⁻⁷, KL regularization (λ_KL = 0.001), and temperature T = 1.0 during generation.
- Evaluation is conducted on held-out benchmarks: AIME 2024&2025 and HLE (math), OlympiadBench (physics), and MedCaseReasoning test set (medicine), all using text-only questions.
- Performance is measured using pass@k and AUC@K, with AUC@K computed via the trapezoidal rule to summarize overall performance across different inference budgets.
Method
The authors leverage a group-based reinforcement learning framework, extending Group Relative Policy Optimization (GRPO), to enhance the diversity of solution strategies in large language models. The overall method operates by reweighting policy update advantages to favor correct but rare solution strategies, thereby mitigating exploration collapse. As shown in the framework diagram, the process begins with a problem input, from which multiple reasoning traces (rollouts) are generated by the language model. These rollouts are then processed through an LLM-based classifier that groups them into strategy clusters based on high-level solution ideas, such as geometric packing or finite differences, rather than surface-level variations. The classification step is critical for identifying solution strategy uniqueness.

The core of the method lies in the advantage calculation, which combines both solution quality and strategy uniqueness. For each problem, the policy generates K rollouts, each receiving a scalar reward from a task-specific verifier. In vanilla GRPO, the group-normalized advantage for a rollout pm,k is computed as zm,k=(rm,k−μm)/(σm+ε), where μm and σm are the mean and standard deviation of rewards within the group. The authors modify this by introducing a uniqueness weight wm,k=1/fm,kα, where fm,k is the size of the strategy cluster to which rollout pm,k belongs, and α is a hyperparameter controlling the reweighting strength. This weight ensures that rollouts belonging to small, rare clusters (e.g., a unique but correct approach) receive a larger effective advantage, while rollouts in large, common clusters are downweighted. The final advantage used for policy updates is the product of the quality-normalized term and the uniqueness weight: advantagem,k=wm,kzm,k.

The training objective remains consistent with GRPO, using the modified advantage term in a policy-gradient objective. The policy parameters are updated to maximize the expected advantage-weighted log-likelihood of the rollouts. This approach effectively encourages the policy to explore and exploit a broader range of high-level solution strategies for each problem, rather than converging to a single dominant mode. The method is designed as a drop-in replacement for the standard GRPO advantage, making it straightforward to integrate into existing reinforcement learning pipelines for language models.
Experiment
- Evaluated pass@k performance across math (AIME 2024/2025, HLE), physics (OlympiadBench-Physics), and medicine (MedCaseReasoning) domains using Qwen2.5-7B; our uniqueness-aware RL method (OURS) consistently outperforms both instruction baseline and GRPO-only SimpleRL, especially at medium-to-large budgets (k ≥ 32), with higher asymptotic accuracy and improved pass@k slope.
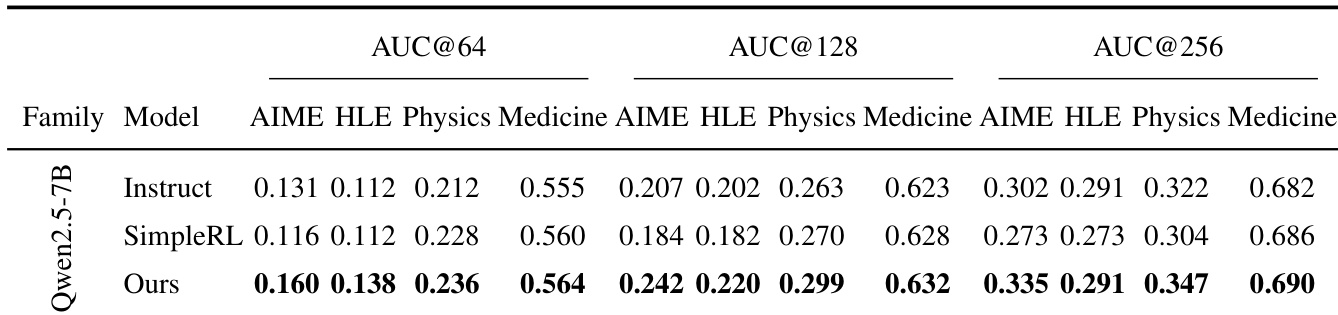
- Achieved highest AUC@K across all domains and budgets (K=64/128/256) on Qwen2.5-7B, with significant gains on challenging AIME and HLE settings (e.g., +0.058 at K=128 on AIME), indicating superior accuracy–coverage trade-off and reduced mode collapse.
- On OLMo-3-7B and Qwen-3-8B, OURS again achieved the best AUC@K on HLE/Physics, outperforming alternative exploration methods (DAPO, Forking Token), demonstrating generalization and complementary benefits from uniqueness-aware training.
- Demonstrated sustained exploration via entropy dynamics: OURS maintains higher and more stable policy entropy during training compared to SimpleRL, which exhibits decreasing entropy, indicating preserved diversity in solution trajectories.
- Introduced cover@n to measure human solution coverage; on 20 challenging AIME problems, OURS achieved higher cover@32 than the instruct baseline on 4 complex problems, including full coverage (100%) on a geometry problem by recovering rare strategies like Symmedian Similarity, and 75% coverage on a combinatorics problem by adding Trail/Flow Viewpoint.
The authors use AUC@K to evaluate the accuracy-coverage trade-off across different models and domains, with higher values indicating better performance. Results show that the proposed method (OURS) consistently achieves the highest AUC@K across all budgets (64, 128, 256) and domains (AIME, HLE, Physics, Medicine) on the Qwen2.5-7B model, outperforming both the Instruct baseline and the SimpleRL baseline, with the largest gains observed in the more challenging AIME and HLE settings.
The authors use AUC@K to evaluate the accuracy-coverage trade-off across different models and methods. Results show that their uniqueness-aware RL method (OURS) achieves the highest AUC@64 and AUC@128 on both HLE and Physics benchmarks for both OLMo-3-7B and Qwen-3-8B models, outperforming both the Instruct baseline and the SimpleRL baseline, with the largest gains observed on the more challenging HLE setting.
