Command Palette
Search for a command to run...
JudgeRLVR:効率的な推論のための最初に判断し、次に生成するアプローチ
JudgeRLVR:効率的な推論のための最初に判断し、次に生成するアプローチ
Jiangshan Duo Hanyu Li Hailin Zhang Yudong Wang Sujian Li Liang Zhao
概要
検証可能な報酬を用いた強化学習(Reinforcement Learning with Verifiable Rewards; RLVR)は、大規模言語モデルにおける推論の標準的な枠組みとして定着している。しかし、最終的な答えの正しさにのみ焦点を当てて最適化を行うと、モデルは無意味で冗長な探索に陥りやすく、構造的な計画ではなく、試行錯誤を徹底的に繰り返す戦略に依存してしまう。長さペナルティのようなヒューリスティックな制約によって冗長性を抑えることは可能であるが、それらはしばしば重要な推論ステップを削除してしまうため、効率性と検証可能性の間に難しいトレードオフが生じる。本論文では、効率的な生成のためには識別能力が前提条件であると主張する。すなわち、正当な解とそうでない解を区別する能力を学習することで、モデルは探索空間を効果的に削減する内部的なガイダンス信号を内面化できる。そこで、判断→生成の二段階アプローチであるJudgeRLVRを提案する。第一段階では、検証可能な答えを持つ解の応答を評価する能力をモデルに学習させる。第二段階では、第一段階で学習したモデルを初期値として、従来の生成用RLVRで微調整を行う。同じ数学領域の訓練データを用いた場合、Vanilla RLVRと比較して、JudgeRLVRはQwen3-30B-A3Bにおいてより優れた品質–効率のトレードオフを実現する。ドメイン内数学問題においては平均正解率が約+3.7ポイント向上し、平均生成長さは約42%短縮された。また、ドメイン外ベンチマークにおいても平均正解率が約+4.5ポイント向上し、汎化性能の向上が確認された。
One-sentence Summary
The authors from Peking University and Xiaomi propose JudgeRLVR, a two-stage reinforcement learning framework that first trains a model to judge verifiable solutions, enabling more efficient reasoning by pruning the search space; this approach improves both accuracy and generation efficiency in Qwen3-30B-A3B, achieving up to +4.5 accuracy gain on out-of-domain math benchmarks with significantly reduced verbosity.
Key Contributions
- The paper identifies a key limitation of Reinforcement Learning with Verifiable Rewards (RLVR): optimizing solely for final-answer correctness leads to verbose, unstructured exploration with excessive backtracking, undermining efficiency without guaranteeing higher-quality reasoning.
- It proposes JudgeRLVR, a two-stage paradigm where a model first learns to judge solution validity before being fine-tuned for generation, enabling it to internalize discriminative priors that prune low-quality reasoning paths without explicit length penalties.
- On Qwen3-30B-A3B, JudgeRLVR achieves +3.7 average accuracy gain with -42% generation length on in-domain math and +4.5 accuracy improvement on out-of-domain benchmarks, demonstrating superior quality-efficiency trade-offs and reduced reliance on explicit backtracking cues.
Introduction
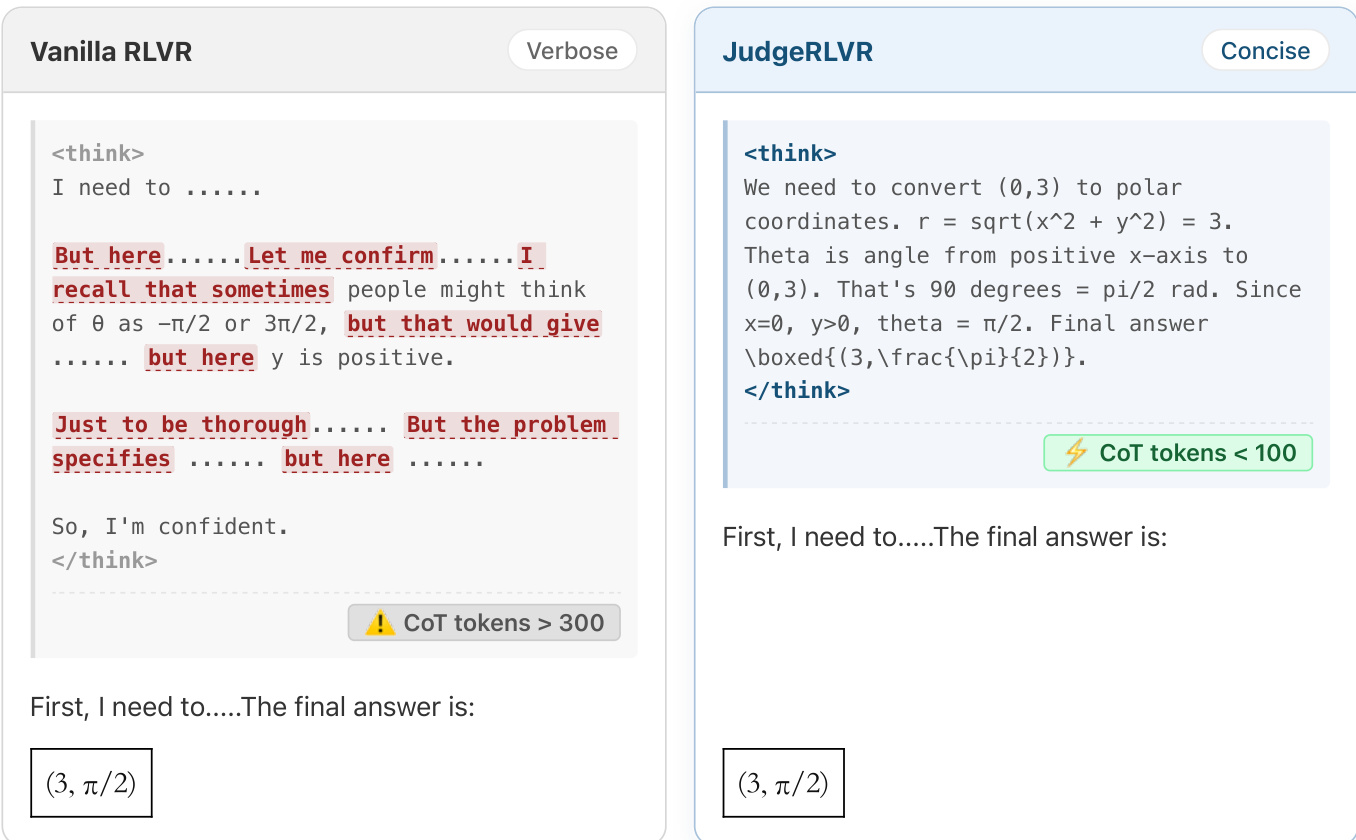
The authors address the challenge of inefficient and verbose reasoning in large language models trained via Reinforcement Learning with Verifiable Rewards (RLVR), where models often resort to trial-and-error exploration instead of structured, goal-directed thinking. While RLVR improves final answer accuracy, it fails to promote high-quality reasoning patterns, leading to low information density and excessive generation length—issues exacerbated by heuristic fixes like length penalties that trade off accuracy for brevity. To overcome this, the authors propose JudgeRLVR, a two-stage training paradigm: first, the model is trained as a judge to discriminate between correct and incorrect solution responses, internalizing a strong signal for valid reasoning; second, the same model is fine-tuned for generation using vanilla RLVR, initialized from the judge. This approach implicitly prunes unproductive reasoning paths without explicit constraints, resulting in more direct, coherent, and efficient reasoning. On Qwen3-30B-A3B, JudgeRLVR achieves a +3.7 accuracy gain and 42% reduction in generation length on in-domain math tasks, along with +4.5 accuracy improvement on out-of-domain benchmarks, demonstrating superior quality-efficiency trade-offs and reduced reliance on backtracking cues.
Dataset
- The dataset comprises math reasoning problems from multiple sources, each with a gold final answer a∗(x), and solution responses z=(o1,…,oT) that include a step-by-step logical process ending in a final answer.
- The final answer a(z) is extracted from the solution response using a deterministic parser, and correctness is determined by comparing a(z) to a∗(x) via a binary label ℓ(x,z)=I(a(z)=a∗(x)).
- The model is trained to judge the correctness of clean solution responses rather than full reasoning trajectories, enabling more precise error detection by avoiding noise from lengthy, distracting CoT sequences.
- The training and evaluation use in-domain math benchmarks: AIME24, AIME25, MATH500, HMMT_feb_2025, and BeyondAIME, all sourced from published works and curated for high-quality reasoning problems.
- Out-of-domain evaluation covers diverse capabilities using benchmarks such as GPQA Diamond (science reasoning), IFEval (instruction following), LiveCodeBenchv6 (coding), MMLU-Redux (general knowledge), and ZebraLogic (logical reasoning).
- The model is trained on a mixture of these datasets with carefully balanced ratios to ensure robust performance across domains, with no explicit cropping strategy applied—data is used as-is after standard preprocessing.
- Metadata for each problem includes source, difficulty level, and problem type, constructed during dataset curation to support fine-grained analysis and evaluation.
Method
The authors leverage a two-stage training paradigm, JudgeRLVR, to enhance reasoning efficiency by decoupling discriminative error awareness from solution generation. The overall framework consists of a judging stage followed by a generating stage, where the model first learns to evaluate the correctness of candidate solutions before being optimized to produce high-quality outputs. This sequential approach is designed to enable the model to internalize valid reasoning patterns, thereby improving generation quality and reducing unnecessary computation.
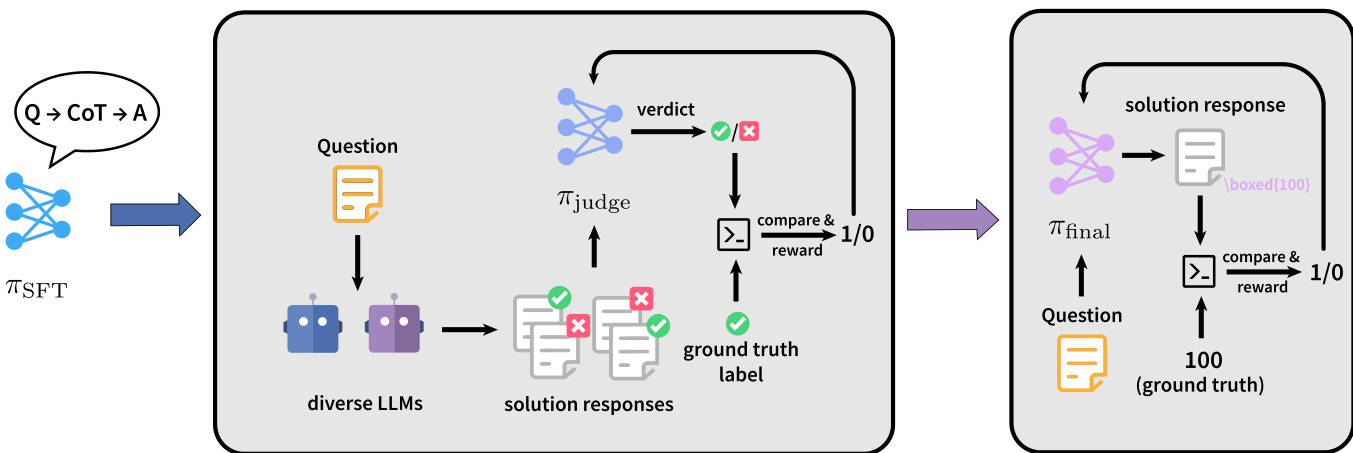
As shown in the figure below, the training pipeline begins with a supervised fine-tuned model, πSFT, which serves as the base for both stages. In the judging stage, the model is trained to act as a critic. Given a problem x and a candidate solution response z, the policy πjudge generates a commentary c that includes the chain-of-thought (CoT) trajectory and a discrete verdict token v∈{0,1}, where 0 indicates an incorrect solution and 1 indicates a correct one. The model is trained on a discriminative dataset Djudge constructed from triplets (x,z,ℓ), where ℓ is the ground truth label derived from comparing the final answer a(z) with the correct answer a∗(x). Data construction involves rollout generation from diverse large language models (LLMs), hard negative mining to focus on moderately difficult problems, and class balancing to ensure equal representation of correct and incorrect solutions. The reward for this stage is binary, based on whether the predicted verdict vi matches the true label ℓ(x,zi), and the policy gradient optimizes both the verdict and the explanatory commentary.
In the generating stage, the model is initialized with the weights from the judging stage and is trained under a vanilla reinforcement learning with verification (RLVR) setting. The policy πfinal generates a solution response z directly from the problem x, producing a CoT trajectory and the final answer a(z). The reward is again a sparse binary signal based on the correctness of the final answer, defined as r=ℓ(x,z)=I(a(z)=a∗(x)). This stage leverages the discriminative knowledge acquired during the judging phase to produce more concise and accurate solutions, as the model has learned to identify and avoid erroneous reasoning paths early in the generation process.
The model architecture used is Qwen3-30B-A3B, a mixture-of-experts (MoE) model, which is first fine-tuned on curated open-source CoT datasets to obtain Qwen3-30B-A3B-SFT. For training, the authors collect a dataset of 113k math problems with gold answers and employ a strict sampling strategy for the judging stage, generating 16 distinct reasoning paths per problem using MiMo-7B RL and the target model. The training algorithm is DAPO, a GRPO-family policy gradient method, with dynamic sampling to filter out trivial problems, a batch size of 256, and a rollout size of n=8. Training uses the AdamW optimizer with a learning rate of 3×10−6, a 10-step warmup, and a training temperature of 1.0, while inference uses a temperature of 0.6.
Experiment
-
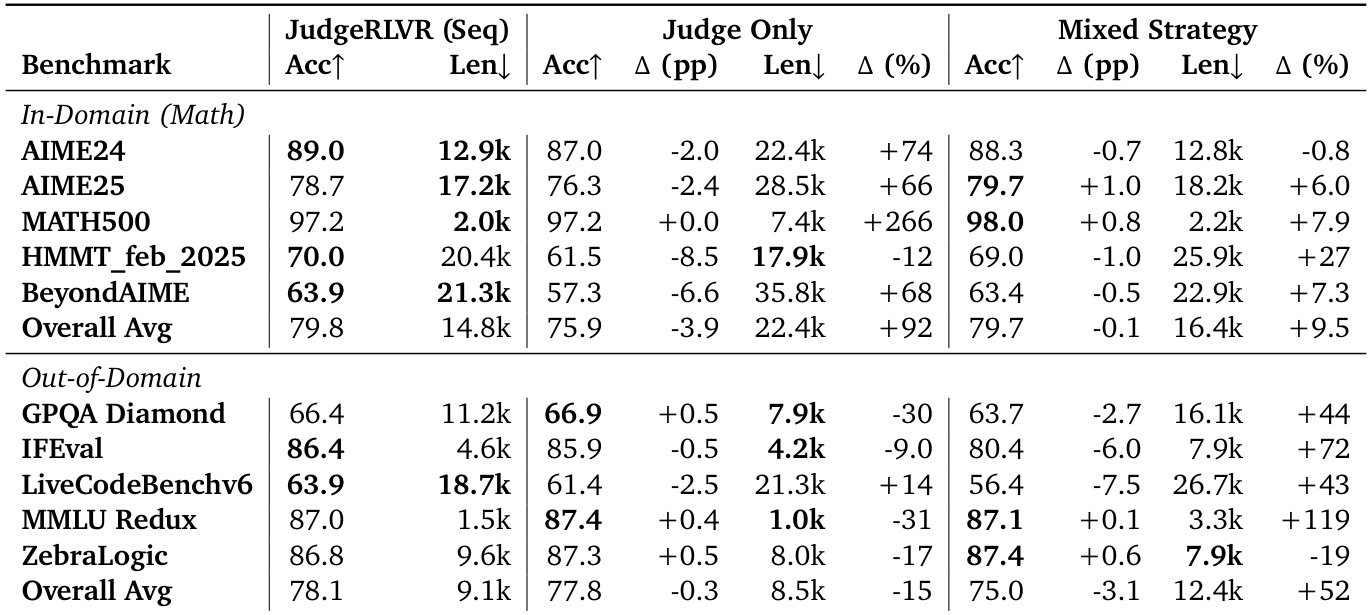
Main experiment: JudgeRLVR vs. Vanilla RLVR and Base SFT on reasoning quality and efficiency. JudgeRLVR achieves higher or comparable accuracy with significantly shorter generation lengths across multiple benchmarks, demonstrating improved quality-efficiency trade-off. On AIME24/25, HMMT_feb_2025, and BeyondAIME, JudgeRLVR improves accuracy while reducing reasoning verbosity; on MATH500, it maintains accuracy with drastic length reduction. On out-of-domain tasks (GPQA Diamond, LiveCodeBenchv6, MMLU-Redux), JudgeRLVR improves accuracy and reduces length, indicating generalization of error-aware reasoning. On IFEval and ZebraLogic, accuracy improves but length increases, reflecting task-specific need for explicit verification.
-
Ablation experiments: Judge Only (judging-only training) degrades accuracy and increases length on in-domain math, showing that judging alone does not improve generation. Mixed Strategy (interleaved judge/generate training) is less stable and often produces longer outputs, indicating that sequential staging is essential for clean policy learning and efficient reasoning.
-
Mechanism verification: Perplexity (PPL) analysis shows a significant increase in Base SFT’s PPL on JudgeRLVR outputs during the judging stage, confirming a style transfer toward error-sensitive reasoning. Transition-word statistics reveal a substantial decrease in backtracking markers (e.g., but, however, wait) during JudgeRLVR’s generating stage, indicating reduced explicit self-correction and internalized verification.
The authors use the table to compare the performance of Base SFT, Vanilla RLVR, and JudgeRLVR across multiple benchmarks, showing that JudgeRLVR achieves higher or comparable accuracy while significantly reducing generation length in most cases. Results show that JudgeRLVR improves the quality-efficiency trade-off by enabling more concise reasoning, particularly in math domains, and demonstrates consistent gains in accuracy and efficiency across diverse tasks.
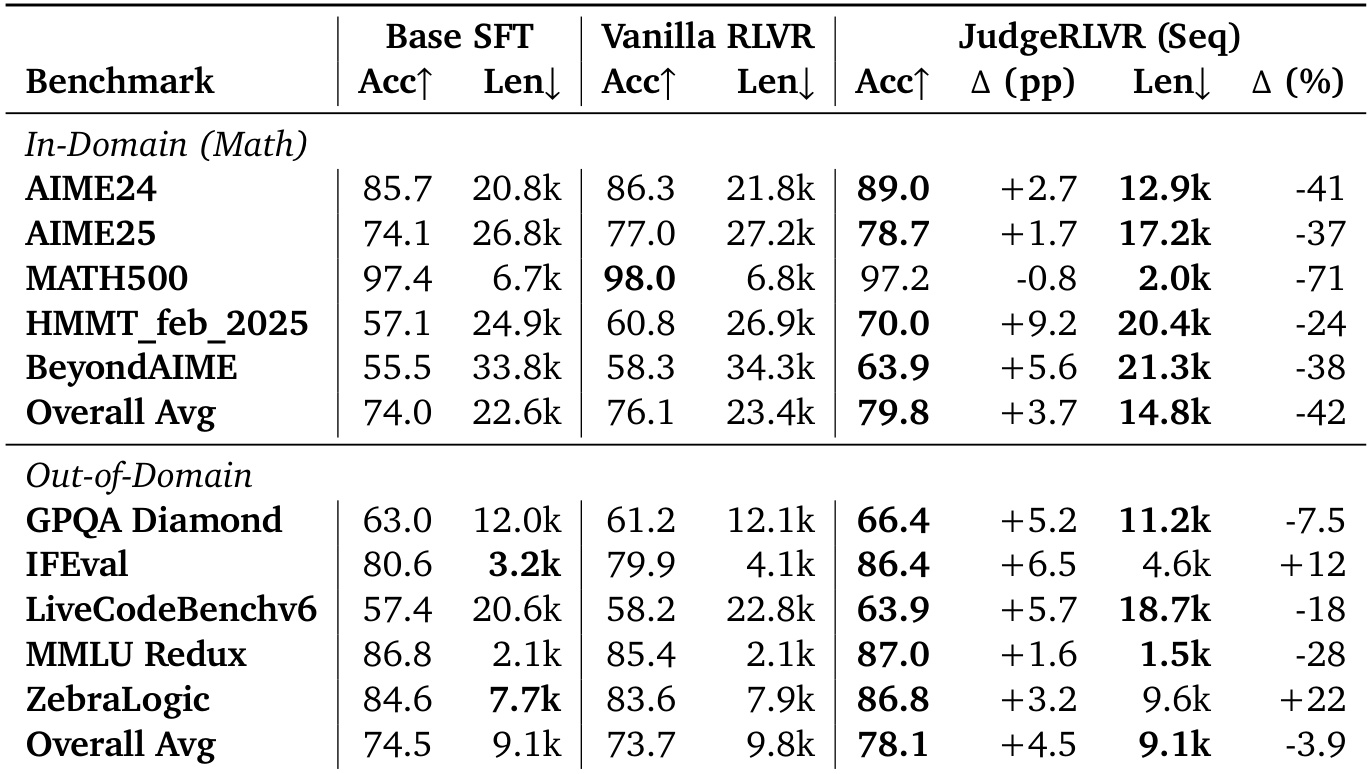
The authors use a two-stage judge-then-generate approach, JudgeRLVR, to improve the quality-efficiency trade-off in reasoning tasks compared to Vanilla RLVR. Results show that JudgeRLVR achieves higher or comparable accuracy while significantly reducing generation length across most benchmarks, indicating more efficient and focused reasoning.
The authors use a two-stage judge-then-generate approach in JudgeRLVR to improve the quality-efficiency trade-off compared to Vanilla RLVR, achieving higher or comparable accuracy while significantly reducing generation length across most benchmarks. Results show that JudgeRLVR consistently outperforms Vanilla RLVR in in-domain math tasks, with substantial gains in accuracy and shorter outputs, and maintains competitive performance on out-of-domain tasks, demonstrating improved reasoning efficiency and generalization.