One-sentence Summary

The Falcon LLM Team proposes learnable per-row and per-column multipliers that dynamically scale weight matrices during training, overcoming the suboptimal equilibrium induced by weight decay and stochastic gradient noise; this adaptive approach outperforms tuned μP multipliers and matches the gains of switching from Adam to Muon, reducing tuning overhead while enabling practical insights into symmetry and width scaling.

Key Contributions

• Weight decay (WD) in large language model pretraining induces a noise-WD equilibrium that constrains weight norms to scale with learning rate and WD hyperparameters, limiting the model's ability to adapt optimal scales to the data. This work identifies the equilibrium norm as a suboptimal artifact and proposes learnable multipliers to escape it.

• The method introduces learnable scalar, per-row, and per-column multipliers to reparametrize weight matrices, enabling the model to learn data-adaptive scales and achieving richer, more diverse representations across residual blocks—outperforming a well-tuned $\mu$μP baseline with reduced tuning overhead.

• Validated on both Adam and Muon optimizers across standard and hybrid attention-SSM architectures, learnable multipliers consistently improve downstream performance, matching the gains from switching optimizers, while raising practical considerations around symmetry and width-scaling.

Introduction

The authors investigate the role of weight decay (WD) in large language model (LLM) training, where it is widely used in optimizers like AdamW and Muon to stabilize training and improve performance. From a stochastic gradient noise perspective, WD maintains a balance with noise-induced weight growth, leading to a predictable equilibrium in weight norms that scales with the learning rate and WD hyperparameter. This equilibrium, however, constrains model weights from learning optimal scales from data, effectively limiting representational capacity. To address this, the authors introduce Learnable Multipliers (LRM), a reparameterization technique that decouples weight scale from optimization hyperparameters by introducing learnable scalar or vector factors applied to matrix layers. This allows weights to adapt their scale freely during training, escaping the noise-WD equilibrium. Experiments show LRMs enable richer, more diverse feature representations across residual blocks and maintain a consistent performance advantage over baselines in long-form pretraining. The approach is robust across architectures—including hybrid attention-SSM models—and optimizers like Adam and Muon, demonstrating broad applicability.

Method

The authors leverage a reparameterization approach to address the suboptimal weight norm equilibrium induced by the interplay between stochastic gradient noise and weight decay in large language model training. This equilibrium constrains the scale of weight matrices, limiting their ability to adapt to data-specific representations. To overcome this, the method introduces learnable multipliers that allow the model to dynamically adjust the scale of its internal representations. The core idea is to decouple the scale of the weight matrices from the noise-WD equilibrium by introducing learnable parameters that can freely adapt to the data distribution.

The framework begins with a scalar multiplier reparameterization, where the effective weight matrix $\overline{W}_{ij}$Wij​ is expressed as $\overline{W}_{ij} = s W_{ij}$Wij​=sWij​, with $s \in \mathbb{R}$s∈R being a learnable scalar. This allows the overall norm of the weight matrix to be adjusted independently of the noise-WD equilibrium, which would otherwise constrain $\|W\|$∥W∥ to a fixed value proportional to $\sqrt{\eta / \lambda}$η/λ​. The scalar multiplier $s$s learns to scale the matrix $W_{ij}$Wij​ such that the full matrix norm $\|\overline{W}\| = s \|W\|$∥W∥=s∥W∥ optimally adapts to the data. This reparameterization is applied to linear layers in the model, enabling the model to escape the suboptimal equilibrium norm.

Building on this, the authors extend the approach to vector multipliers, introducing per-row and per-column scaling parameters to further refine the scale adaptation. The reparameterization becomes $\overline{W}_{ij} = r_i W_{ij} c_j$Wij​=ri​Wij​cj​, where $r_i \in \mathbb{R}^{d_{\text{out}}}$ri​∈Rdout​ and $c_j \in \mathbb{R}^{d_{\text{in}}}$cj​∈Rdin​ are learnable vectors. This allows individual row and column norms of the weight matrix to be independently scaled, addressing the hypothesis that even the norms of individual rows and columns are constrained by the noise-WD equilibrium. The gradients of the reparameterized matrix $W_{ij}$Wij​ and the multipliers $r_i$ri​, $c_j$cj​ are derived using the chain rule, showing that the row and column multipliers accumulate gradients across their respective dimensions, which reduces gradient noise and prevents the Brownian expansion that necessitates weight decay.

The method is designed to be compatible with standard training frameworks. During inference, the learnable multipliers can be merged with their corresponding weight matrices into the effective matrix $\overline{W}_{ij}$Wij​, eliminating any memory or latency overhead. During training, two implementation strategies are considered: one that explicitly uses the reparameterized expression in the forward pass, relying on automatic differentiation, and another that uses effective matrices in the forward and backward passes while manually handling the dynamics of the multipliers on the optimizer level. The latter approach reduces the throughput drop associated with the additional parameters.

The authors also address the issue of symmetry-induced instabilities that arise when multiple learnable factors appear in a product. These symmetries, such as multiplicative and normalization symmetries, can lead to unbounded growth in the norms of certain parameters without affecting the model output, causing numerical instability. To mitigate this, a small weight decay is applied to the multipliers, which stabilizes the training without significantly impacting performance.

Experiment

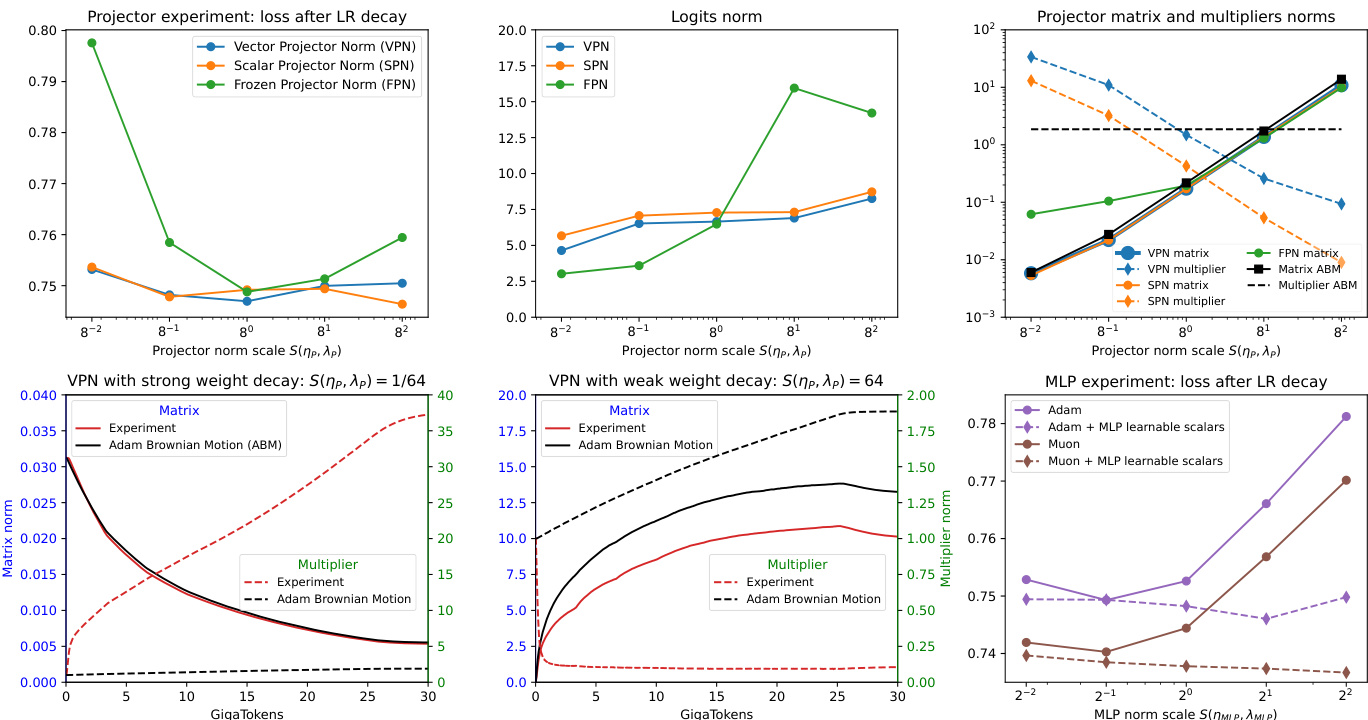
• Projector and MLP experiments validate that matrix layers are trapped in noise-WD equilibrium, while learnable multipliers (scalar/vector) enable scale adaptation, maintaining stable logit and residual norms under extreme norm scaling. On the LM head and MLP blocks, configurations with fixed projector norms suffer performance drops at extreme scales, whereas multiplier-equipped versions maintain stable performance and logit norms.
• Multiplier experiments show that learnable multipliers adjust their scale independently of noise-WD equilibrium, as confirmed by ABM simulations where multiplier trajectories diverge from noise-driven dynamics. This confirms multipliers are not constrained by equilibrium scaling.
• Depth-wise and width-wise scale analysis reveals that scalar multipliers enable increasing residual output norms across model depth and promote feature scale diversity in attention and MLP layers, with attention and SSM dt projections showing layer-specific scale specialization.
• Width scaling experiments demonstrate that matrix norms remain constant across model widths, breaking standard LR-only μP scaling rules. Learnable multipliers automatically adapt to width, achieving stable activation norms (projector, SSM dt, attention QK) and scaling approximately as predicted (d⁻¹, d⁻²), indicating effective automatic adaptation.
• Gradient clipping experiments show that including multiplier gradients in the norm computation causes excessive clipping and performance degradation; excluding them restores stability and improves training, highlighting the need for careful integration of learnable multipliers.
• Multiplier tuning ablation shows that learnable multipliers consistently outperform non-learnable configurations, with the best performance achieved when both learnable multipliers and tuned learning rates are used. Performance gains persist across optimizers (Adam, Muon), confirming generalizability.
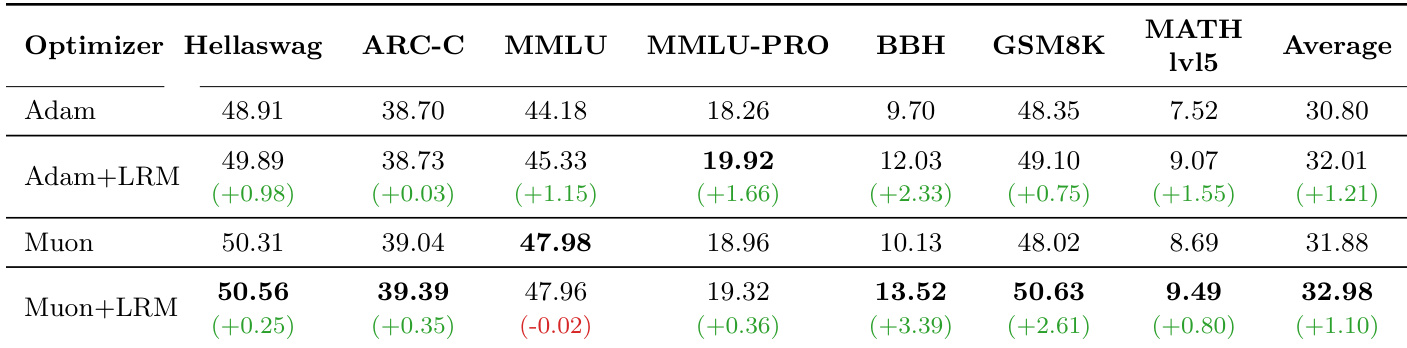
• Long training validation (200GT) confirms sustained performance gains from learnable multipliers: +1.21% (Adam) and +1.10% (Muon), with larger improvements on reasoning benchmarks (BBH, MATH, GSM8K) than knowledge benchmarks (ARC-C, MMLU), suggesting differential impact on model capabilities.

The authors use a table to compare the performance of models with and without learnable multipliers across different optimizers and benchmarks. Results show that adding learnable multipliers consistently improves performance, with the Muon+LRM configuration achieving the highest average score of 32.98%, outperforming both Adam and Muon baselines. The gains are most pronounced in reasoning tasks like BBH, MATH, and GSM8K, while knowledge-based benchmarks show more modest improvements.

The authors use a table to compare scaling recipes for model width, showing that only the multiplier-based approach maintains constant activation and update norms across widths. Results show that learnable multipliers enable stable scaling by adjusting their values as $d^{-1}$d−1, while standard LR-only scaling leads to diverging activations and vanishing update strengths.