Command Palette
Search for a command to run...
多様性か精度か?次トークン予測の深い考察
多様性か精度か?次トークン予測の深い考察
Haoyuan Wu Hai Wang Jiajia Wu Jinxiang Ou Keyao Wang Weile Chen Zihao Zheng Bei Yu
概要
最近の研究進展により、強化学習(RL)が大規模言語モデル(LLM)の推論能力を著しく向上させることを示している。しかしながら、このようなRL訓練の有効性は、事前学習モデルのトークン出力分布によって定義される探索空間に大きく依存している。本論文では、標準的な交差エントロピー損失を、単一ステップのエピソード内で適用された特定のポリシー勾配最適化の例として再解釈する。事前学習分布がその後のRLにおける探索可能性にどのように影響するかを体系的に検討するため、オンポリシーRLの原則を教師あり学習に適応する一般化された事前学習目的関数を提案する。次トークン予測を確率的決定過程として定式化することで、多様性と精度の明示的なバランスを実現する報酬設計戦略を導入する。本手法は、正の報酬スケーリング係数を用いて真値トークンへの確率集中を制御し、ランクに配慮したメカニズムにより、高ランクと低ランクの負例トークンを非対称に扱う。これにより、事前学習済みのトークン出力分布を再設計し、RLにより有利な探索空間を提供する方法を検証する。最終的に、エンドツーエンドの推論性能を向上させる。直感的には分布エントロピーが高いほど効果的な探索が可能になるとされるが、本研究では精度志向の事前分布を導入することで、RLにとってより優れた探索空間が得られることを明らかにした。
One-sentence Summary
The authors from Tencent and The Chinese University of Hong Kong propose a generalized pre-training objective that adapts on-policy RL principles to supervised learning, using reward shaping with positive scaling and rank-aware mechanisms to balance diversity and precision in token distributions, thereby creating a more favorable exploration space for RL and improving end-to-end reasoning performance, contrary to the conventional belief that higher entropy aids exploration.
Key Contributions
-
We reinterpret the standard cross-entropy loss as a single-step policy gradient optimization, enabling a systematic study of how the pre-trained model's token-output distribution shapes the exploration space for downstream reinforcement learning.
-
We propose a generalized pre-training objective that integrates on-policy RL principles into supervised learning, using a reward scaling factor to control probability concentration on ground-truth tokens and a rank-aware mechanism to asymmetrically suppress high- and low-ranking negative tokens.
-
Experiments show that a precision-oriented prior—contrary to the common belief that high entropy aids exploration—leads to a more effective exploration space, significantly improving end-to-end reasoning performance in subsequent RL stages.
Introduction
The authors investigate the role of next-token prediction in shaping the behavior of large language models during reinforcement learning (RL), particularly in reasoning tasks. While prior work has treated pre-training as a supervised process separate from RL, the authors highlight that cross-entropy loss—commonly used in pre-training—can be interpreted as a form of on-policy policy gradient optimization, establishing a theoretical link between pre-training and RL. This insight reveals that the output distribution from pre-training, shaped by the reward structure of the loss, implicitly defines the model’s exploration space during subsequent RL, influencing which reasoning paths are pursued. However, traditional pre-training methods fix the reward structure to favor precision by concentrating probability mass on the ground-truth token, potentially limiting diversity and constraining exploration. The authors’ main contribution is a generalized pre-training objective that explicitly controls the trade-off between diversity and precision through reward shaping: they introduce a positive scaling factor to modulate the concentration of probability on the correct token and apply asymmetric suppression to negative tokens based on their rank. This approach allows systematic tuning of the pre-training policy, and counterintuitively, they find that a precision-oriented prior—rather than high entropy—leads to better RL exploration and improved end-to-end reasoning performance.
Method
The authors leverage a policy-gradient framework to reinterpret the standard cross-entropy loss in next-token prediction as a specific instance of reinforcement learning (RL) optimization within a single-step episode. This perspective enables a systematic investigation into how the pre-trained model’s token-output distribution shapes the exploration space for subsequent RL training. The core idea is to treat the generation of each token as an independent decision-making process, where the language model acts as a stochastic policy πθ that selects the next token from the vocabulary V based on the current context st=X<t. The training objective is formulated as maximizing the expected immediate reward, which simplifies to a single-step return Jt(θ∣st)=Eat∼πθ(⋅∣st)[r(st,at)]. This formulation ensures that the reward depends solely on the immediate state-action pair, aligning with the policy gradient derivation for episodic tasks.
Within this framework, the standard cross-entropy objective is expressed as a policy gradient with an intrinsic reward function rCE(st,at)=sg(πθ(at∣st)1(at=xt)), where the stop-gradient operator sg(⋅) ensures that the reward depends only on the current step. This reward structure implicitly balances diversity and precision: high-probability ground-truth tokens receive a large reward inversely proportional to their probability, while all negative tokens are assigned zero reward. The authors generalize this objective by introducing a reward-shaping strategy that explicitly controls the trade-off between diversity and precision through two mechanisms.
First, a positive reward scaling factor is introduced to modulate the influence of the ground-truth token. The modified positive reward is defined as rˉpos(st,at)=sg((πθ(at∣st)1)(1−πθ(at∣st))β), where β controls the global entropy of the distribution. When β<0, the reward is amplified, leading to aggressive concentration of probability mass on the ground truth and reduced entropy. Conversely, β>0 attenuates the reward, allowing the model to maintain a flatter distribution with higher entropy. This mechanism enables fine-grained control over the global exploration potential during pre-training.
Second, the authors propose a rank-aware negative reward mechanism to regulate local entropy. Let Kt denote the set of top-k predicted tokens. Negative rewards are assigned asymmetrically: high-ranking negative tokens (those in Kt but not the ground truth) receive a reward λ~, while low-ranking negative tokens (outside Kt) receive a reward λ^. This design prevents overconfidence in the ground truth by preserving probability mass for plausible alternatives, while simultaneously suppressing the tail of the distribution to encourage concentration on the most likely candidates. The generalized reward function combines these components as rˉ(st,at)=rˉpos(st,at)⋅1(at=xt)+rˉneg(st,at)⋅1(at=xt), where rˉneg(st,at)=λ~⋅1(at∈Kt∧at=xt)+λ^⋅1(at∈/Kt∧at=xt).
This reward-shaping strategy is embedded within a supervised learning objective, effectively adapting on-policy RL principles to pre-training. The resulting generalized loss function allows for the systematic exploration of how reshaping the token-output distribution during pre-training influences the subsequent RL stage. The authors demonstrate that precision-oriented priors—characterized by reduced global entropy and suppression of low-probability tokens—yield a more favorable exploration space for RL, ultimately enhancing end-to-end reasoning performance. The framework is compatible with architectures that perform iterative internal computation before token emission, such as latent-reasoning models and loop transformers, and can serve as an uncertainty-aware learning signal to guide adaptive computation policies.
Experiment
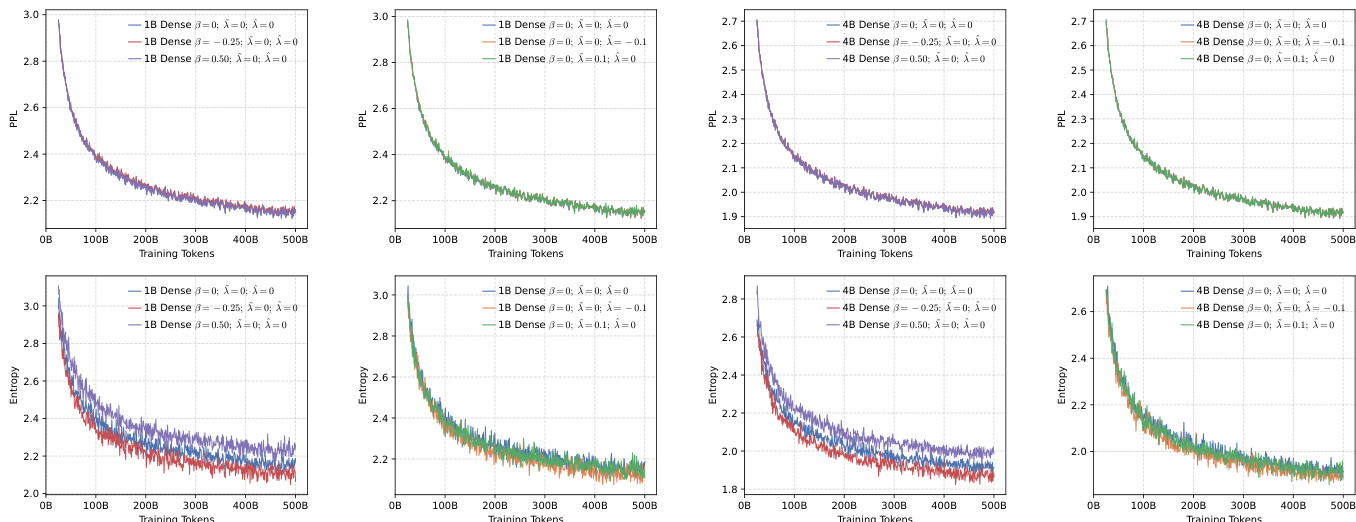
- Pre-training evaluation validates the effectiveness of the generalized training objective in balancing diversity and precision across dense and MoE architectures, with lower perplexity and stable convergence observed across models.
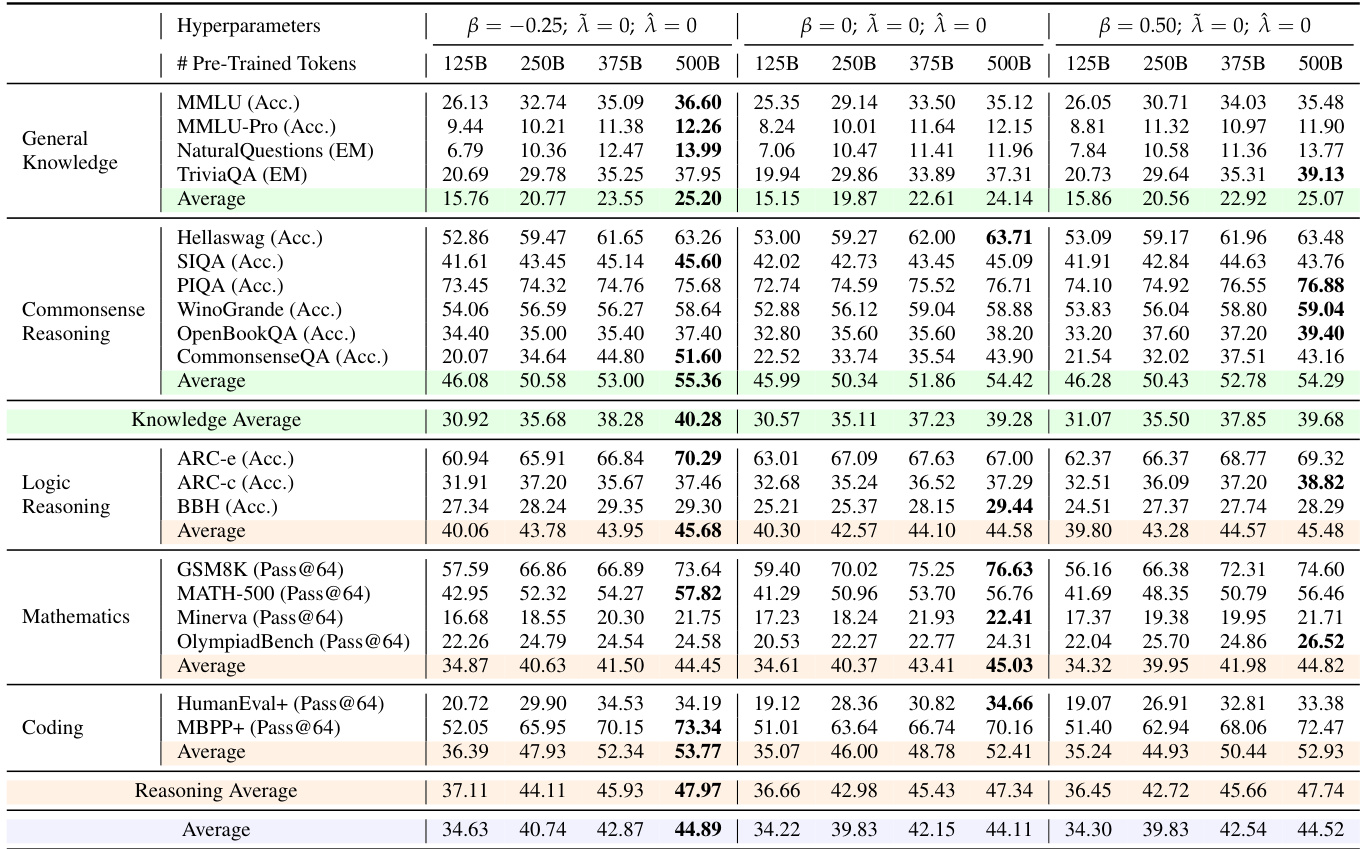
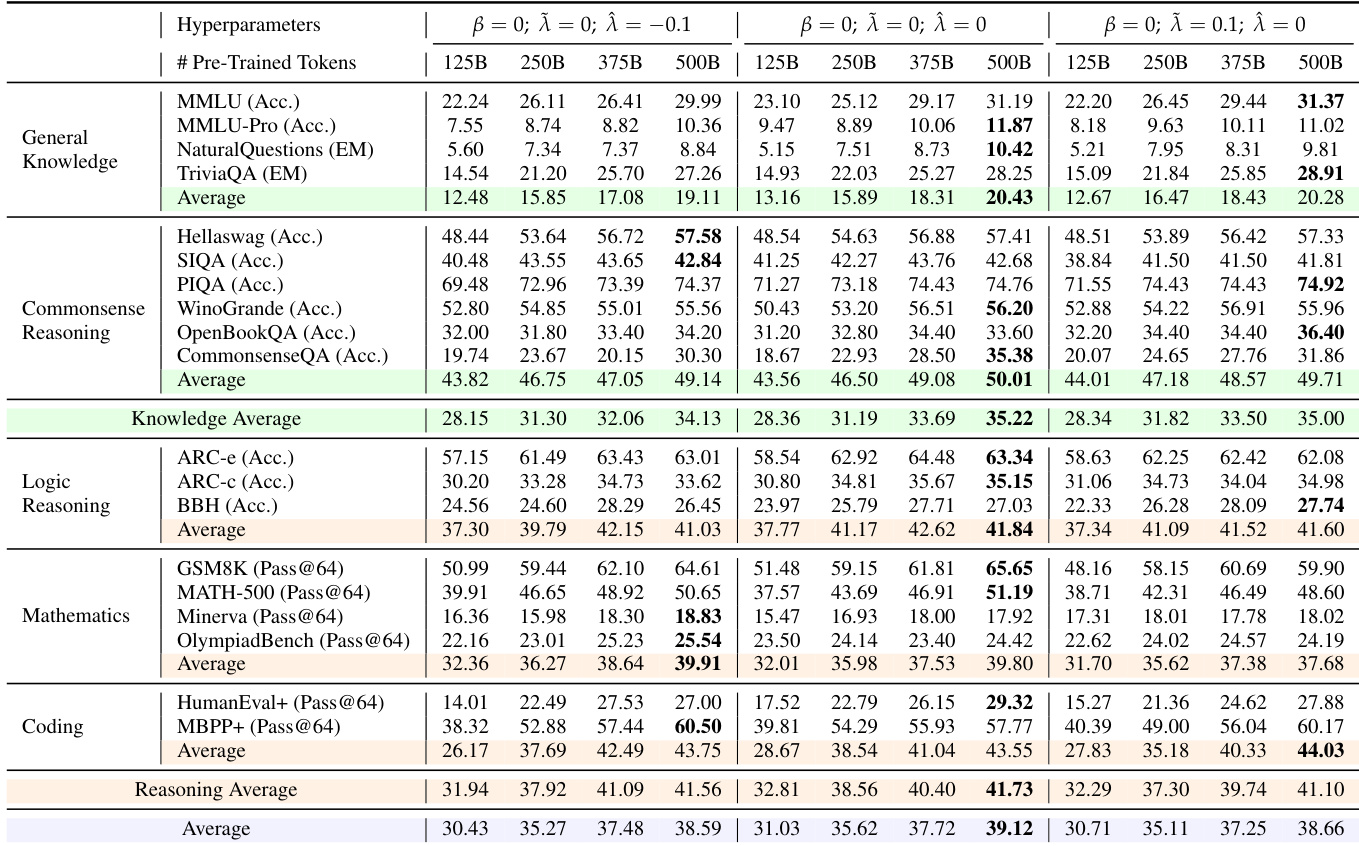
- Mid-training experiments demonstrate that setting β = -0.25 consistently improves performance on knowledge and reasoning tasks over the baseline, while local entropy control via λ^=−0.1,λ~=0 enhances scaling behavior.
- Reinforcement learning results show that global low-entropy settings (β = -0.25) and local high-entropy configurations (λ^=−0.1,λ~=0) yield superior performance on mathematics and coding benchmarks, with higher Avg@128, Cons@128, and Pass@64 scores.
- Pass@k analysis confirms that prioritizing precision, rather than global diversity, leads to higher upper-bound performance in mathematics and code generation, with stable output diversity maintained.
- On MATH-500 and OlympiadBench, the 10B-A0.5B MoE model with β = -0.25 achieved Pass@64 of 68.4 and 52.1, surpassing the baseline by 12.3 and 9.7 points respectively.
- On HumanEval+, the 10B-A0.5B MoE model with λ^=−0.1,λ~=0 achieved Pass@64 of 74.2, outperforming the baseline by 8.5 points.
The authors use a range of model architectures, including dense and MoE models, to evaluate the impact of different reward configurations on training dynamics and performance. Results show that configurations promoting precision, such as setting β = -0.25 or using local entropy control with λ̂ = -0.1, consistently yield superior performance across pre-training, mid-training, and reinforcement learning stages.

The authors use a range of benchmarks to evaluate model performance across general knowledge, commonsense reasoning, logic reasoning, mathematics, and coding tasks. Results show that the configuration with β = -0.25 consistently achieves the highest scores across most evaluation metrics, particularly in mathematics and coding, indicating that promoting precision through lower global entropy leads to superior performance.
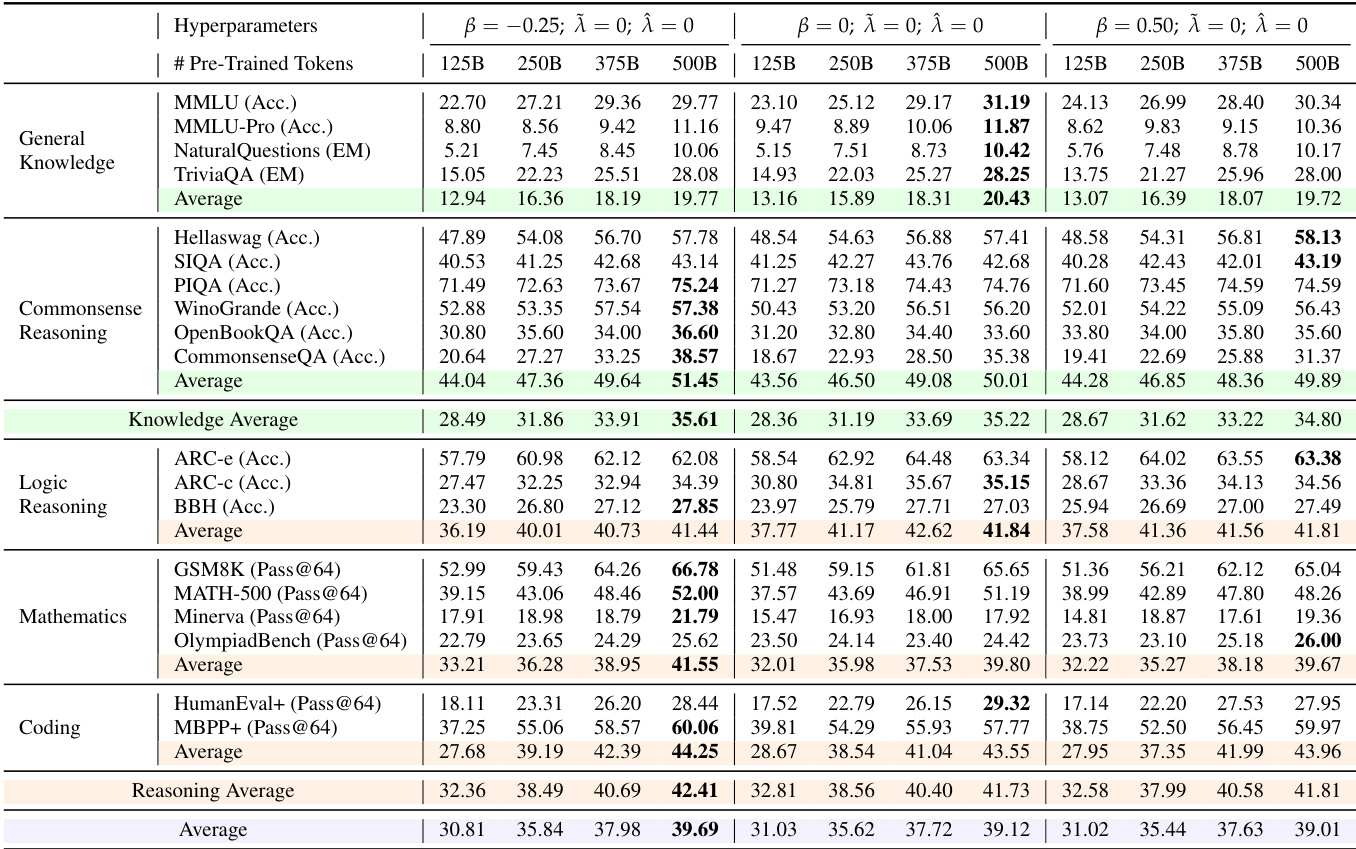
The authors use a range of benchmarks to evaluate base models across general knowledge, commonsense reasoning, logic reasoning, mathematics, and coding. Results show that the configuration with β = 0, λ̃ = 0, and λ̂ = 0 consistently achieves the highest performance across most tasks, particularly in mathematics and coding, where it attains the best Pass@64 scores.
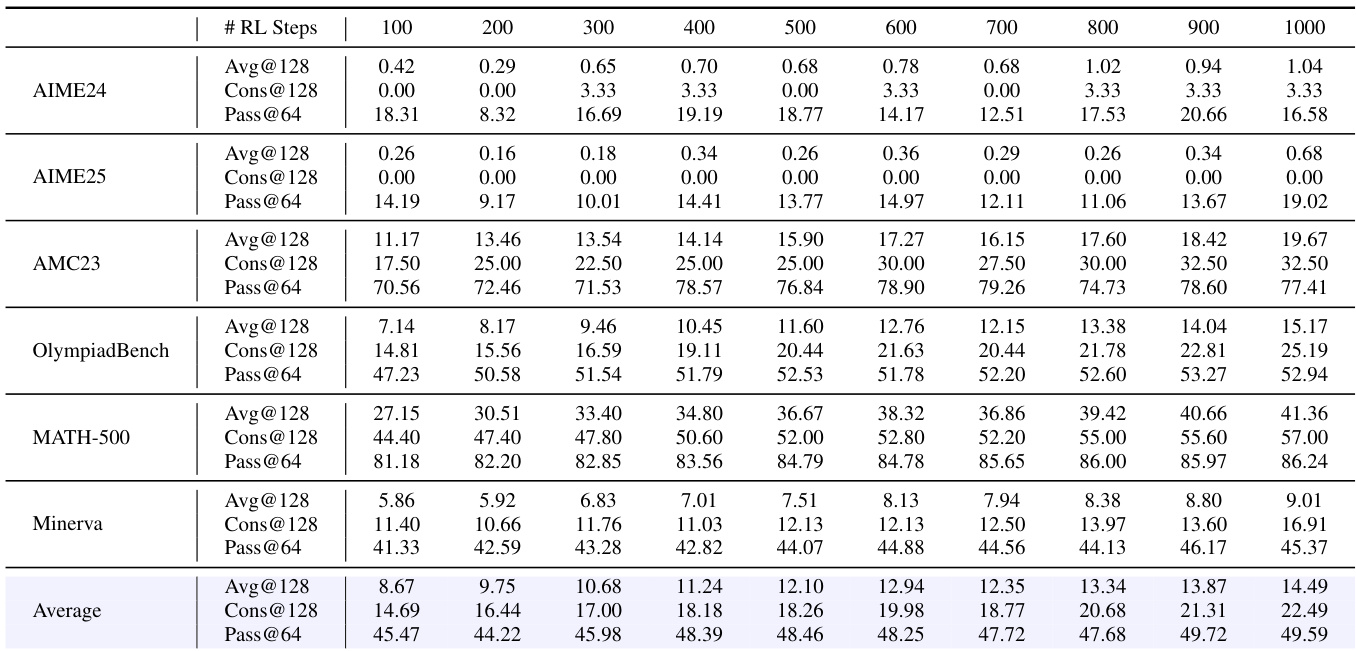
The authors use the Pass@64 metric to evaluate the performance of a 4B dense model during reinforcement learning training on mathematical reasoning tasks. Results show that the model's Pass@64 score increases steadily from 18.31 at 100 RL steps to 16.58 at 1000 steps, indicating improved capability in generating correct solutions over time. The average Pass@64 across all benchmarks reaches 49.59 at the final step, demonstrating significant progress in reasoning performance.
The authors use a range of benchmarks to evaluate model performance across general knowledge, commonsense reasoning, logic reasoning, mathematics, and coding. Results show that configurations with lower global entropy (β = -0.25) consistently achieve higher performance across most tasks, particularly in mathematics and coding, while maintaining sufficient output diversity. The data further indicate that strategies promoting precision, either globally or locally, lead to better performance and scaling behavior, especially in larger models.