Command Palette
Search for a command to run...
DTS:デコード木スケッチを活用した大規模推論モデルの性能向上
DTS:デコード木スケッチを活用した大規模推論モデルの性能向上
Zicheng Xu Guanchu Wang Yu-Neng Chuang Guangyao Zheng Alexander S. Szalay Zirui Liu Vladimir Braverman
概要
大規模推論モデル(LRM)は、複雑な推論タスクにおいて優れた性能を発揮する一方で、過剰な推論(overthinking)の問題に直面し、推論の連鎖(CoT)が極めて長くなりがちである。この現象は推論コストの増加を招き、精度の低下を引き起こす可能性もある。我々の分析から、推論の長さと精度の間に明確な逆相関が存在することが明らかになった。複数回の確率的デコードにおいて、短い推論経路は一貫して最も高い正解率を示すのに対し、長くなるほど誤りや重複が蓄積される。理想的には、推論空間の全探索によって最適な短い推論経路を発見できるが、木構造を持つ推論空間はシーケンス長に応じて指数関数的に拡大するため、完全な探索は現実的ではない。この課題に対処するため、我々はDTSを提案する。DTSはモデルに依存しないデコードフレームワークであり、エントロピーの高いトークンのみに選択的に分岐を実施することで推論空間の概要を描き、早期停止戦略を用いて最短の完了した推論経路を選定する。このアプローチにより、追加の訓練や教師信号を必要とせずに、効率性と精度の両方を向上させる近似最適解を実現できる。DeepSeek-R1-Distill-Qwen-7Bおよび1.5Bモデルを用いたAIME2024およびAIME2025データセット上の実験では、DTSが精度を最大8%向上させ、平均推論長を23%短縮し、重複頻度を12%低減することを確認した。これらは、DTSがスケーラブルかつ効率的なLRM推論を実現できることを示している。
Summarization
Researchers from Rice University, University of Minnesota, and Johns Hopkins University propose DTS, a model-agnostic decoding framework that reduces overthinking in Large Reasoning Models by selectively exploring high-entropy decision points and prioritizing shorter reasoning paths. DTS improves accuracy by up to 8% and cuts reasoning length by 23% without retraining, enabling more efficient and accurate AI reasoning on complex tasks.
Key Contributions
- DTS introduces a training-free, model-agnostic decoding framework that reduces overthinking in Large Reasoning Models by selectively exploring high-entropy decision points in the reasoning process.
- It constructs a compact decoding tree using parallel auto-regressive generation and applies early stopping to identify the shortest complete and accurate reasoning path.
- Experiments show DTS improves accuracy by up to 8%, reduces average reasoning length by 23%, and decreases repetition frequency by 12% on AIME2024 and AIME2025 benchmarks.
Introduction
Large Reasoning Models (LRMs) excel at complex tasks by generating step-by-step chain-of-thought (CoT) reasoning, but they often suffer from overthinking—producing long, redundant reasoning paths that increase inference cost and hurt accuracy. Prior work has attempted to address this through training-based methods like supervised fine-tuning or reinforcement learning on compressed or length-penalized data, or via adaptive pruning mechanisms. However, these approaches require additional labeled data and training, limiting scalability, while train-free methods often lack consistent performance gains.
The authors leverage the observation that shorter reasoning paths are empirically more accurate, forming a tree-structured reasoning space during autoregressive generation where optimal paths are short but buried in an exponentially large search space. To efficiently approximate the best path without training, they propose DTS (Decoding Tree Sketching), a model-agnostic decoding framework that dynamically constructs a compact reasoning tree at inference time.
- Uses next-token entropy to selectively branch only at high-uncertainty tokens, reducing search complexity.
- Applies early stopping to return the shortest completed reasoning path, aligning with the observed accuracy-length anti-correlation.
- Operates entirely at decoding time with GPU parallelism, enabling training-free, plug-and-play deployment across models.
Method
The authors leverage a novel decoding strategy called Decoding Tree Sketching (DTS) to efficiently identify the shortest reasoning path in Large Reasoning Models (LRMs), capitalizing on the observed anti-correlation between reasoning length and accuracy. Rather than exhaustively exploring the exponentially growing space of all possible reasoning sequences, DTS constructs a pruned decoding tree that selectively expands branches only at high-uncertainty tokens, thereby approximating the optimal short path while maintaining computational feasibility.
The core mechanism of DTS hinges on an adaptive branch function F(x,ξ) that determines whether to generate a single token or spawn multiple branches at each decoding step. This decision is governed by the entropy H(v) of the next-token distribution P(v)=f(x,ξ), where f denotes the LRM. When H(v)≥τ, indicating high uncertainty, DTS selects the top-K most probable tokens to initiate new branches; otherwise, it samples a single token. Formally:
F(x,ξ)={{v1,…,vK∣pv1,…,pvK≥p~K}{v1}, v1∼P(v)if H(v)≥τ,if H(v)<τ,where p~K is the K-th largest probability in P(v). This entropy-based gating allows DTS to focus computational resources on regions of the reasoning space where the model is uncertain, while proceeding deterministically in confident regions.
As shown in the figure below, the decoding tree grows in a breadth-first manner, with each node representing a token and edges denoting transitions. Branching occurs only at steps t1 and t2, where entropy exceeds the threshold τ, and the top two tokens are selected for expansion. Low-entropy steps proceed linearly, preserving efficiency.
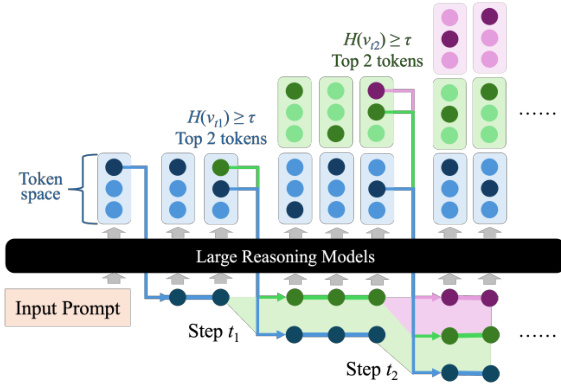
At each time step t, DTS maintains a set of active reasoning sequences Tt, initialized as T0=∅. For each sequence ξ∈Tt, the model applies F(x,ξ) to generate next tokens, which are appended to form new sequences. The set is then updated as:
Tt+1={ξ⊕vi∣vi∈F(x,ξ), ξ∈Tt}.This process continues iteratively, with all branches generated in parallel to exploit GPU acceleration, ensuring scalability.
Early termination is triggered as soon as any branch emits the ending token ⟨e⟩, following the principle that shorter reasoning paths yield higher accuracy. Formally, DTS stops at step t if ⋁ξ∈Tt1[⟨e⟩∈ξ], and returns the first completed sequence as the final output.
An illustrative example is shown in the figure below, where DTS processes the prompt “What’s the area of a rectangle with length 12 and width 9?”. Branching occurs at steps t1 and t2, generating multiple reasoning paths. The purple branch terminates first with the correct answer “area= 12×9=108”, which is returned as the final output.
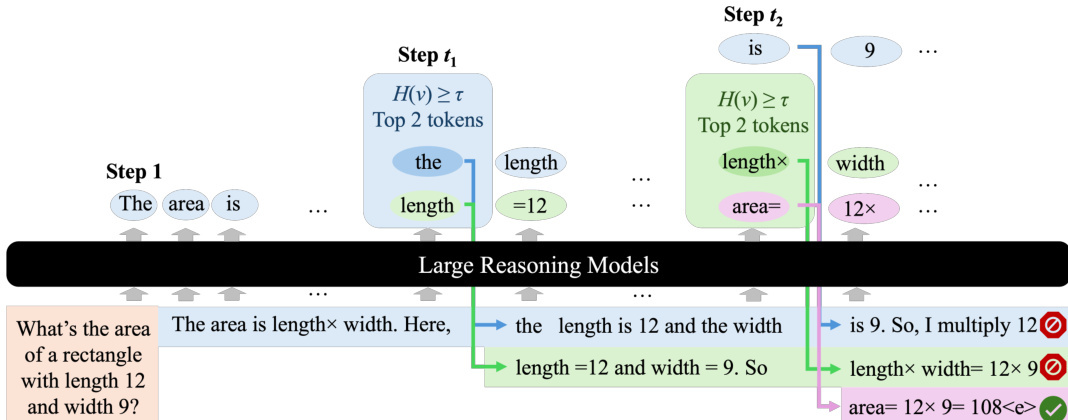
The algorithm follows a breadth-first search over the sketched tree, guaranteeing that the shortest valid reasoning path is identified. All active branches are expanded in parallel, enabling efficient and scalable inference without sacrificing the quality of the reasoning output.
Experiment
Respond strictly in English.
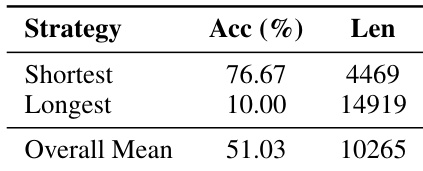
The authors use 100 stochastic decodes per AIME24 problem to evaluate reasoning trajectories, finding that selecting the shortest response yields 76.67% accuracy with significantly fewer tokens than the longest or mean responses. Results show a strong anti-correlation between response length and accuracy, indicating that verbose reasoning degrades performance. This supports the motivation for DTS, which prioritizes shorter, more efficient reasoning paths to improve both accuracy and efficiency.
The authors use the DTS framework to improve reasoning performance and efficiency for DeepSeek-R1-Distill-Qwen models on AIME2024 and AIME2025. Results show DTS consistently increases accuracy by 4% to 8% while reducing response length by 17% to 29% compared to standard inference, with the 7B model achieving a 7.66% average accuracy gain and 22.96% length reduction. These improvements hold across both model sizes and datasets, demonstrating DTS’s effectiveness in balancing performance and efficiency without training.
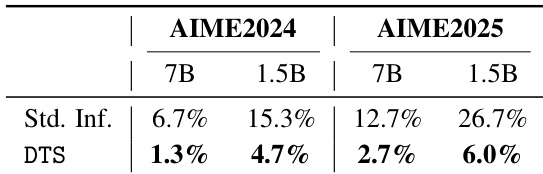
The authors use DTS to reduce endless repetition in reasoning trajectories, showing that it lowers repetition rates across both AIME2024 and AIME2025 benchmarks for 7B and 1.5B models. Results show DTS cuts repetition from 6.7% to 1.3% on AIME2024 for the 7B model and from 26.7% to 6.0% on AIME2025 for the 1.5B model. This confirms DTS effectively prunes repetitive paths by favoring shorter, completed reasoning traces.