One-sentence Summary

Researchers from Tsinghua University and Alibaba propose Elastic Attention, a dynamic sparsity adaptation method using a lightweight Attention Router to adjust computation modes per head, outperforming static hybrid approaches in long-context LLMs with minimal retraining.

Key Contributions

• Elastic Attention introduces a lightweight Attention Router that dynamically assigns each attention head to either full or sparse computation mode based on input context, enabling adaptive sparsity without altering the pretrained model’s backbone parameters.
• The method addresses the limitation of static hybrid attention by learning to allocate sparsity according to task sensitivity—preserving performance on sparsity-sensitive tasks like QA while leveraging efficiency on sparsity-robust tasks like summarization.
• Evaluated on three long-context benchmarks using Qwen3 and Llama-3.1-8B-Instruct, Elastic Attention achieves superior performance with only 12 hours of training on 8×A800 GPUs, while maintaining inference efficiency through a fused kernel and minimal parameter overhead (0.27M per layer).

Introduction

The authors leverage Elastic Attention to tackle the quadratic complexity bottleneck in large language models during long-context inference. Prior sparse attention methods either rely on static patterns or fixed sparsity ratios, limiting adaptability across diverse tasks and requiring careful hyperparameter tuning. Their key contribution is a lightweight Attention Router that dynamically assigns each attention head to sparse or full computation modes based on input characteristics, enabling test-time sparsity adaptation without retraining the base model. This approach achieves strong performance and efficiency gains with minimal training overhead.

Dataset

The authors use a combined training dataset built from five sources to train Qwen3-(4B/8B) and Llama-3.1-8B-Instruct models, targeting both sparsity-sensitive and sparsity-robust tasks. Here’s how the dataset is structured and used:

• Dataset Composition and Sources:

  • ChatQA2-Long-SFT-data: Covers single-document and multihop QA (sparsity-sensitive).
  • MuSiQue: Multihop QA benchmark (sparsity-sensitive).
  • CoLT-132K: Code completion and in-context learning tasks (sparsity-robust).
  • GovReport: Long-document summarization (sparsity-robust).
  • XSum: Short summarization (sparsity-robust).

• Key Subset Details:

  • Total token count: ~0.74B.
  • Sequence lengths: 8K to 64K tokens.
  • Task weighting: Sparsity-robust tasks use t=1.0; sparsity-sensitive tasks use t=0.7.

• Usage in Training:

  • Trained on 8×A800 GPUs, each run under 12 hours.
  • Mixture ratios reflect task categories (sparsity-sensitive vs. sparsity-robust) via t-values.
  • Hyperparameters detailed in Table 6; full training setup in Appendix D.

• Processing and Configuration:

  • No explicit cropping mentioned; sequences span up to 64K tokens.
  • Metadata not constructed separately; task categories drive weighting.
  • Attention modes tested: Streaming Sparse Attention (SSA) and XAttention (XA, τ=0.9).
  • Head computation modes denoted as “{Retrieval Head mode}-{Sparse Head mode}”, e.g., FA-SSA.

Method

The authors leverage a modular framework centered on the Elastic Attention mechanism, which introduces a lightweight Attention Router to dynamically adjust the sparsity of attention computation within transformer layers. The overall architecture, as illustrated in the framework diagram, integrates this module into a standard transformer block without modifying the backbone model's parameters. The core of the approach lies in the Attention Router, which operates analogously to a Mixture-of-Experts (MoE) gating mechanism. It processes the key hidden states ($\boldsymbol{x}_{K} \in \mathbb{R}^{s \times H \times d'}$xK​∈Rs×H×d′) to perform head-wise routing, determining whether each attention head should employ Full Attention (FA) or Sparse Attention (SA) computation. This dynamic assignment enables the model to adapt its overall sparsity based on the input task regime.

The Attention Router's architecture, detailed in the diagram, consists of two primary components: a Task MLP and a Router MLP. The process begins with pooling the key hidden states along the sequence dimension to obtain a task representation ($\boldsymbol{x}_{K}^{\prime} \in \mathbb{R}^{H \times d'}$xK′​∈RH×d′). This pooled representation is then fed into both the Task MLP and the Router MLP. The Task MLP infers task-specific characteristics, while the Router MLP uses these representations to generate a head-wise routing logit matrix ($\boldsymbol{z} \in \mathbb{R}^{H \times 2}$z∈RH×2). This logit matrix is converted into a binary decision ($r_{\text{hard}}^{(\ell,h)} \in \{0,1\}$rhard(ℓ,h)​∈{0,1}) for each head, indicating the selected computation mode (FA or SA). The routing decisions are then used to assign each attention head to its respective computation path.

To optimize the Attention Router, the authors employ a continuous relaxation scheme based on the Gumbel-Softmax strategy, which allows for differentiable training while approximating discrete routing decisions. This is achieved by applying the Gumbel-Softmax to the routing logits to obtain a soft routing matrix ($r_{\text{soft}}^{(\ell)} \in \mathbb{R}^{H \times 2}$rsoft(ℓ)​∈RH×2). Hard routing decisions are derived from this soft matrix using an arg max operation. To address the non-differentiability of the arg max function, a straight-through estimator (STE) is used, enabling gradient flow through the soft routing distribution during the backward pass while preserving the hard routing behavior in the forward pass. The training objective is designed to minimize the language modeling loss while simultaneously optimizing the model's sparsity ratio ($\Omega_{\text{MSR}}$ΩMSR​) to meet task-specific constraints, using a min-max optimization framework with trainable Lagrange multipliers to decouple the sparsity-performance trade-offs.

For efficient deployment, the framework utilizes a fused attention kernel that processes retrieval and sparse heads simultaneously in a single forward pass. This design eliminates the need for data rearrangement and reduces kernel launch overhead, which is critical for high-throughput inference on long-context sequences. The fused kernel leverages thread-block level branching, where each thread block dynamically retrieves its assigned head's computation mode from routing metadata, allowing for a unified kernel launch and optimal GPU hardware scheduling. This approach ensures that the computational overhead of the Attention Router is minimal, adding only 0.27M parameters per layer, thereby preserving inference efficiency and computational cost.

Experiment

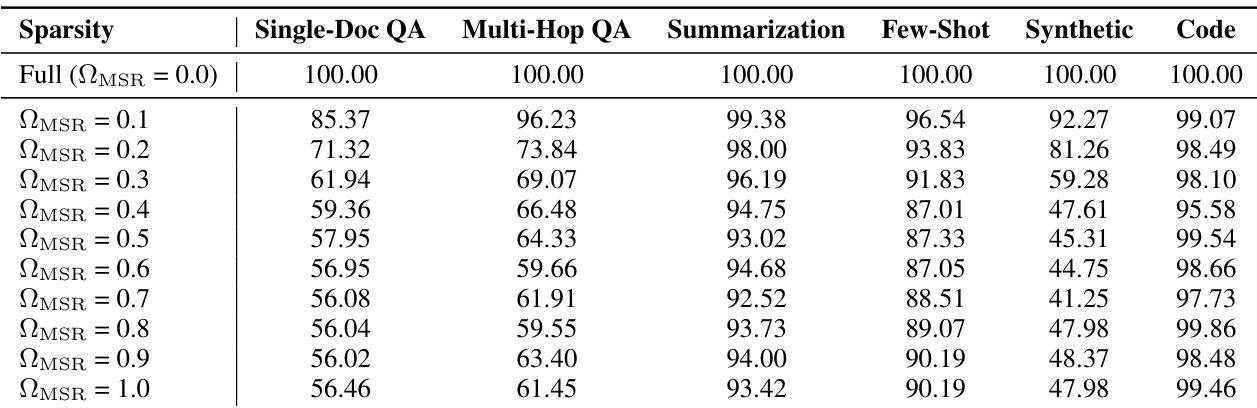
• Evaluated impact of Ω_MSR on Llama3.1-8B-Instruct across LongBench tasks, revealing two categories: sparsity-robust (e.g., summarization) and sparsity-sensitive (e.g., QA), enabling dynamic attention mode selection.
• On LongBench-E and RULER, Elastic Attention outperformed baselines (e.g., InfLLM-V2, MoBA) with average Ω_MSR ~0.65–0.85, achieving best performance at 256K tokens (68.51 on RULER) while maintaining 1.51× speedup (FA-XA) or 3.28× speedup with extreme sparsity (XA-SSA).
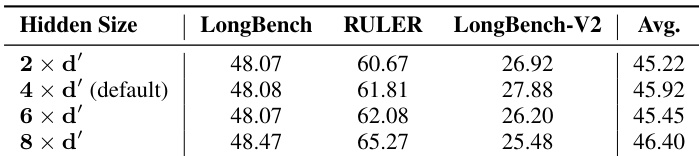
• Ablation confirmed Task MLP enhances task discrimination (reduced cosine similarity), and ×4 hidden size in MLPs offers optimal performance-efficiency trade-off.
• Target sparsity tuning (t_sen=0.7, t_rob=1.0) balanced performance and efficiency; lower t_sen (e.g., 0.4) boosted accuracy but reduced inference gains.
• Router latency negligible (avg. 0.196 ms), stable across 512–1M tokens; boundary-pooling (first/last 100 tokens) optimized task identification without noise.
• On LongBench-V2, Elastic Attention (FA-XA/FA-SSA) achieved top average scores; Qwen3-4B with XA-SSA retained near-backbone performance (gap <1 point) with full sparsity.
• Error analysis showed superior precision in retrieving key context segments, avoiding hallucinations seen in baselines on legal, policy, and narrative tasks.

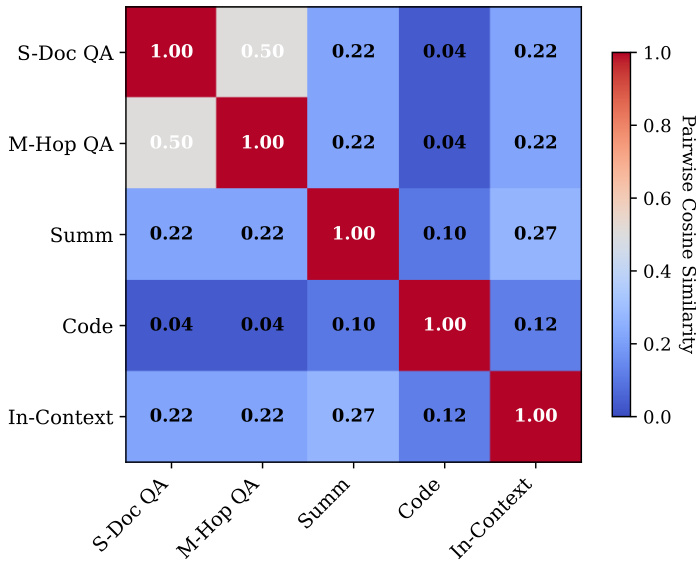
The authors use a heatmap to visualize pairwise cosine similarity between task representations before and after processing by the Task MLP. Results show that the Task MLP significantly reduces inter-task similarity, indicating improved task discrimination. This suggests the model effectively disentangles task-specific features, enabling more accurate attention routing decisions.

The authors investigate the impact of varying $\Omega_{\text{MSR}}$ΩMSR​ on downstream tasks using the Llama3.1-8B-Instruct model, evaluating performance across LongBench tasks. Results show that sparsity-sensitive tasks like QA and Code exhibit significant performance drops as $\Omega_{\text{MSR}}$ΩMSR​ increases, while sparsity-robust tasks such as Summarization remain stable, indicating task-dependent sensitivity to attention sparsity.

The authors investigate the impact of varying the hidden size of the Attention Router on model performance across multiple benchmarks. Results show that increasing the hidden size from 2×d′ to 4×d′ improves average performance, with the 4×d′ setting achieving the highest scores on RULER and LongBench-V2. However, further increasing the hidden size to 8×d′ leads to a decline in performance, indicating that the default 4×d′ setting provides the optimal balance between performance and efficiency.

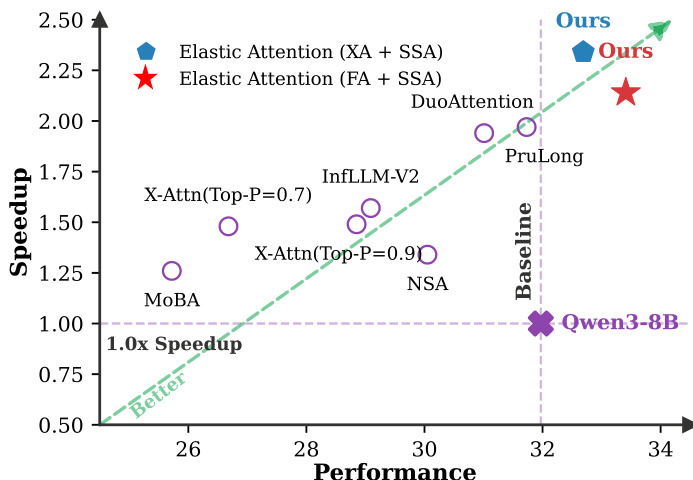
Results show that Elastic Attention achieves the highest performance and speedup among all compared methods, outperforming baselines like DuoAttention, PruLong, and InfLLM-V2. The method establishes a superior Pareto frontier, balancing high performance with efficient inference across different sparsity levels.

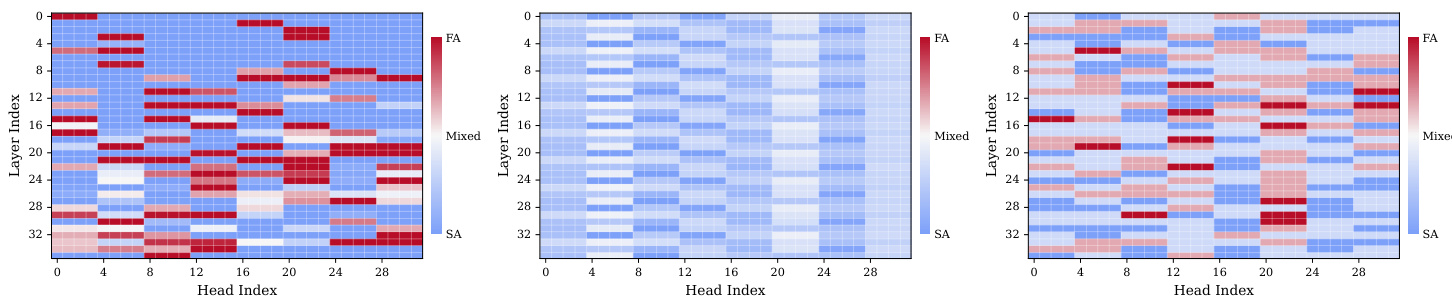
The authors use a heatmap visualization to analyze the attention computation modes across different layers and heads in a language model. The results show that certain heads, particularly in the middle to higher layers, are consistently activated in full-attention (FA) mode across all tasks, indicating they function as retrieval heads. Other heads exhibit task-specific switching behavior, while the majority are consistently routed to sparse attention (SA), demonstrating a clear division in attention mechanisms based on task requirements.